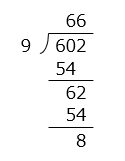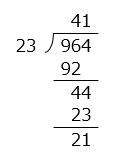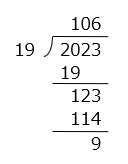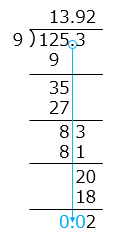算数【基本】余りのある計算
問1
商と余りが正しくない式を①~⑤より選びなさい。
① 11 ÷ 4 = 2 あまり 3
② 18 ÷ 7 = 1 あまり 11
③ 102 ÷ 9 = 10 あまり 12
④ 52 ÷ 6 = 8 あまり 4
⑤ 29 ÷ 8 = 3 あまり 5
- 答え
- ②, ③
- 解き方
- ※余りはわる数より小さくなります!
②(誤)18 ÷ 7 = 1 あまり 11 ⇒ (正)18 ÷ 7 = 2 あまり 4
③(誤)102 ÷ 9 = 10 あまり 12 ⇒ (正)102 ÷ 9 = 11 あまり 3
問2
筆算を使って計算しなさい。
(1)602 ÷ 9 =
- 答え(1)
- 66 あまり 8
- 解き方(1)
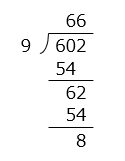
(2)964 ÷ 23 =
- 答え(2)
- 41 あまり 21
- 解き方(2)
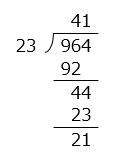
(3)2023 ÷ 19 =
- 答え(3)
- 106 あまり 9
- 解き方(3)
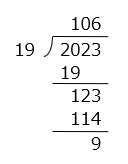
(4)61334 ÷ 213 =
- 答え(4)
- 287 あまり 203
- 解き方(4)

問3
筆算を使って計算しなさい。商と余りの小数点の位置に注意しましょう。
(1)29.53 ÷ 0.8 =
(商は整数で求めなさい)
- 答え(1)
- 36あまり0.73
- 解き方(1)

(2)125.3 ÷ 9 =
(商は小数第2位まで求めなさい)
- 答え(2)
- 13.92あまり0.02
- 解き方(2)
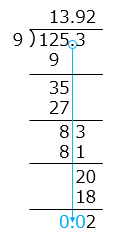
(3)2.5 ÷ 0.41 =
(商は小数第2位まで求めなさい)
- 答え(3)
- 6.09あまり0.0031
- 解き方(3)

(4)58.1 ÷ 1.8 =
(商は小数第1位まで求めなさい)
- 答え(4)
- 32.2あまり0.14
- 解き方(4)

(5)0.05 ÷ 0.7 =
(商は小数第2位まで求めなさい)
- 答え(5)
- 0.07あまり0.001
- 解き方(5)

問4
50cmのリボンがあります。これを7cmずつに切っていくと、7cmのリボンは何本取れますか。
- 答え
- 7本
- 解き方
- 50 ÷ 7 = 7(本) あまり 1(cm)
あまりは7cmより短いので本数にいれない
問5
20枚のクッキーを1日に3枚ずつ食べていくと、クッキーは何日で食べ終わりますか。
- 答え
- 7日
- 解き方
- 20 ÷ 3 = 6(日) あまり 2(枚)
あまった2枚を食べるためにはさらに1日必要である。よって、6 + 1 = 7(日)
問6
整数Aと整数Bがあります。AをBで割ったときのあまりを( A, B )と表すことにします。例えば、Aが10で、Bが7のとき、10 ÷ 7 = 1 あまり 3なので、( 10, 7 )= 3と表します。
(1)( 39, 11 )を求めなさい。
- 答え(1)
- 6
- 解き方(1)
- 39 ÷ 11 = 3 あまり 6
よって、6
(2)( ( 78, 16 ), ( 28, 5 ) )を求めなさい。
- 答え(2)
- 2
- 解き方(2)
- 78 ÷ 16 = 4 あまり 14 より、( 78, 16 ) = 14
28 ÷ 5 = 5 あまり 3 より、( 28, 5 ) = 3
( ( 78, 16 ), ( 28, 5 ) ) = ( 14, 3 )
14 ÷ 3 = 4 あまり 2 より、( ( 78, 16 ), ( 28, 5 ) ) = 2
(3)( ( 104, 32 ), ( 104, 9 ) )を求めなさい。
- 答え(3)
- 3
- 解き方(3)
- 104 ÷ 32 = 3 あまり 8 より、( 104, 32 ) = 8
104 ÷ 9 = 11 あまり 5 より、( 104, 9 ) = 5
( ( 104, 32 ), ( 104, 9 ) ) = ( 8, 5 )
8 ÷ 5 = 1 あまり 3 より、( ( 104, 32 ), ( 104, 9 ) ) = 3
問7
(1)ある数を18で割ると、商は5で、余りは3になりました。ある数を求めなさい。
- ヒント
- ※除法の原理
ある数AをBで割ったとき、商をC、余りをDとすると、
A = B × C + D
と表すことができる
- 答え
- 93
- 解き方
- ある数は、
18 × 5 + 3 = 93
(2)ある数を234で割ると、商が5で、余りが67になりました。ある数を求めなさい。
- 答え
- 1237
- 解き方
- ある数は、5 × 234 + 67 = 1237
問8
1枚84円の切手を1000円で買えるだけ買いました。切手は何枚買えて、お金はいくら余りましたか。
- 答え
- 買えた切手:11枚、余ったお金:76円
- 解き方
- 1000 ÷ 84 = 11 あまり 76
問9
7で割ると3余る整数で100に最も近い整数を求めなさい。
- 答え
- 101
- 解き方
- 7の倍数より3大きい数で100に最も近い数
100に近い7の倍数をいくつか挙げると、91、98、105
それぞれの数に3を足すと、94、101、108
100に最も近い数は101
問10
\(\boxed{ }\) に当てはまる数を答えなさい。
1917 ÷ \(\boxed{ }\) = 35 あまり 27
- 答え
- 54
- 解き方
- \(\boxed{ }\) = (1917 – 27) ÷ 35 = 54
問11
\(\boxed{ }\) に当てはまる数を答えなさい。
\(\boxed{ }\) ÷ 2.9 = 2.7 あまり 0.17
- 答え
- 8
- 解き方
- \(\boxed{ }\) = 2.7 × 2.9 + 0.17 = 8