算数【応用】売買

問１

定価 4000 円の商品を定価の 90 % で売ったところ、原価の 20 % の利益を得ました。この商品の原価はいくらですか。ただし、消費税は考えません。

答え

3000 円

解き方

この商品の売値は、4000 × 0.9 = 3600 [円]

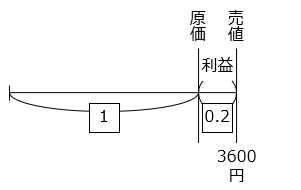
原価を \(\boxed{1}\) とすると、利益は \(\boxed{0.2}\) と表すことができ、次の式が成り立つ。
\(\boxed{1}\) + \(\boxed{0.2}\) = 3600
\(\boxed{1.2}\) = 3600
\(\boxed{1}\) = 3600 ÷ 1.2 = 3000 [円]

【別解】式をつくる
原価を □ 円とすると、次の式が成り立つ。
3600 – □ = 0.2 × □
1.2 × □ = 3600
□ = 3000 [円]

問２

ある品物を原価の 2 割の利益を見込んで定価をつけ、さらにその定価の 1 割引で売ると、利益は 100 円になりました。この品物の原価はいくらですか。

答え

1250 円

解き方

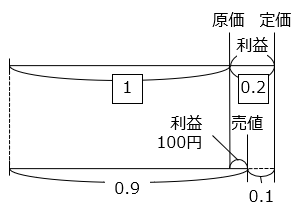
原価を \(\boxed{1}\) とすると、定価は \(\boxed{1.2}\) と表すことができ、売値は \(\boxed{1.2}\) × 0.9 = \(\boxed{1.08}\) となる。
よって、次の式が成り立つ。
\(\boxed{1.08}\) – \(\boxed{1}\) = 100
\(\boxed{0.08}\) = 100
\(\boxed{1}\) = 100 ÷ 0.08 = 100 × \(\dfrac{25}{2}\) = 1250 [円]

【別解】式をつくる
原価を □ 円とすると、
定価：1.2 × □ [円]
売値：1.2 × □ × 0.9 = 1.08 × □ [円]
と表すことができ、次の式が成り立つ。
1.08 × □ – □ = 100
0.08 × □ = 100
□ = 100 × \(\dfrac{25}{2}\) = 1250 [円]

問３

ある品物に原価の 2 割の利益を見込んで定価をつけました。しかし売れなかったので 320 円の値引きをして売ったところ、280 円の利益がありました。この品物の原価は何円ですか。

答え

3000 円

解き方

原価を \(\boxed{1}\) とすると、次の式が成り立つ。
\(\boxed{0.2}\) = 280 + 320 = 600
\(\boxed{1}\) = 600 ÷ 0.2 = 3000 [円]

【別解】式をつくる
原価を □ 円とすると、
定価：1.2 × □ [円]
売値：1.2 × □ – 320 [円]
と表すことができ、次の式が成り立つ。
1.2 × □ – 320 = □ + 280
0.2 × □ = 600
□ = 3000 [円]

問４

ある商品に原価の 20 % の利益を見込んで定価をつけました。しかし売れないので、定価の 20 % 引きで売ったところ、600 円の損をしました。この商品の原価は何円ですか。

答え

15000 円

解き方

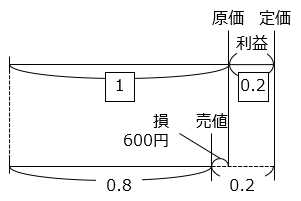
原価を \(\boxed{1}\) とすると、売値は \(\boxed{1.2}\) × 0.8 = \(\boxed{0.96}\) と表すことができる。
よって、次の式が成り立つ。
\(\boxed{1}\) – \(\boxed{0.96}\) = 600
\(\boxed{0.04}\) = 600
\(\boxed{1}\) = 600 ÷ 0.04 = 600 × 25 = 15000 [円]

【別解】式をつくる
原価を □ 円とすると、
定価：1.2 × □ [円]
売値：1.2 × □ × 0.8 = 0.96 × □ [円]
と表すことができ、次の式が成り立つ。
□ – 0.96 × □ = 600
0.04 × □ = 600
□ = 600 × 25 = 15000 [円]

問５

400 個の品物を 1 個 600 円で仕入れ、仕入れ値の 3 割増しの定価をつけて売りました。途中から定価の 1 割り引きにして売ったところすべて売れ、利益は全部で58740 円になりました。定価で売った品物は何個ですか。

答え

230 個

解き方

定価：600 × 1.3 = 780 [円]
割引後の売値：780 × 0.9 = 702 [円]
【つるかめ算を使う】
すべての品物を定価の 1 割引きで売った場合の利益は、
( 702 – 600 ) × 400 = 40800 [円]
となるが、実際の利益は 58740 円 より、定価で売った個数は、
( 58740 – 40800 ) ÷ ( 780 – 702 ) = 230 [個]

【別解①】面積図で考える
定価で売った場合、1 個の利益は 780 – 600 = 180 [円]
一方、割引後の 1 個の利益は 702 – 600 = 102 [円]

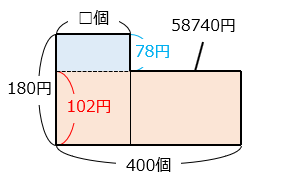
全て割引後の売値で売った場合の利益は 　 = 102 × 400 = 40800 [円]
実際の利益は 58740 円より、　 = 58740 – 40800 = 17940 [円]
よって、割り引いて売った品物の個数（□）は、
17940 ÷ 78 = 230 [個]

【別解②】消去算を使う
定価で売った個数を A、1 割引きで売った個数を B とすると、以下の式が成り立つ。
A + B = 400 ・・・ ㋐
( 780 – 600 ) × A + ( 702 – 600 ) × B = 58740
180 × A + 102 × B = 58740
90 × A + 51 × B = 29370 ・・・ ㋑
㋑ – ㋐ × 51 より、
( 90 – 51 ) × A = 29370 – 400 × 51 = 8970
39 × A = 8970
A = 230 [個]

【別解③】式をつくる
定価で売った個数を □ 個とすると、次の式が成り立つ。
( 780 – 600 ) × □ + ( 702 – 600 ) × ( 400 – □ ) = 58740
180 × □ + 102 × ( 400 – □ ) = 58740
( 180 – 102 ) × □ = 58740 – 40800
78 × □ = 17940
□ = 230 [個]

問６

1000 円で仕入れた品物に □ % の利益を見込んで定価をつけ、売れました。次に同じ品物をまた 1000 円で仕入れたときに、30 % の利益を見込んで定価をつけましたが、売れなかったので、定価の 10 % 引きで売ったところ、前回よりも 30 円利益が下がりました。

□ に当てはまる数を答えなさい。

答え

20

解き方

次に仕入れたときの売値は、1000 × 1.3 × 0.9 = 1170 [円]

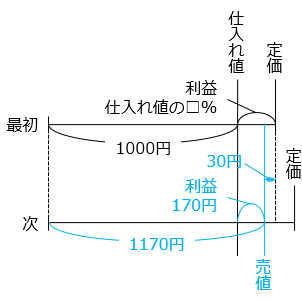
よって、最初に売ったときの利益は 170 + 30 = 200 [円] より、
□ = 200 ÷ 1000 × 100 = 20 [%]

【別解】式をつくる
最初に仕入れたときに見込んだ利益を □ % とすると、このときに得た利益は、
1000 × \(\dfrac{□}{100}\) = 10 × □ [円]
次に仕入れたときの売値は、
1000 × 1.3 × 0.9 = 1170 [円]
より、得た利益は 1170 – 1000 = 170 [円]
よって、次の式が成り立つ。
10 × □ = 170 + 30 = 200
□ = 20 [%]

問７

A 商店と B 商店では、同じ品物を同じ金額で仕入れて、それぞれ次のように考えて定価をつけました。

【A 商店】　仕入れ値の 3 割が利益になるように定価をつけた。

【B 商店】　定価の 2 割が利益になるように定価をつけた。

その結果、A 商店の定価は B 商店の定価よりも 40 円高くなりました。

（１）B 商店の定価は、仕入れ値の何倍にあたりますか。

答え（１）

1.25 倍

解き方（１）

仕入れ値を □ 円とすると、B 商店の定価は次のように表すことができる。
□ ÷ 0.8
= □ ÷ \(\dfrac{4}{5}\)
= □ × \(\dfrac{5}{4}\) = □ × 1.25
よって、1.25 倍

（２）この品物の仕入れ値は何円ですか。

答え（２）

800 円

解き方（２）

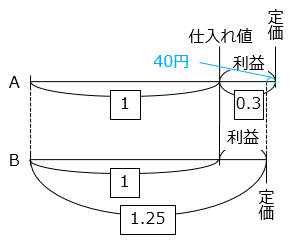
仕入れ値を \(\boxed{1}\) とすると、A 商店の定価は \(\boxed{1.3}\)、B 商店の定価は \(\boxed{1.25}\) と表すことができるので、次の式が成り立つ。
\(\boxed{1.3}\) – \(\boxed{1.25}\) = 40
\(\boxed{0.05}\) = 40
\(\boxed{1}\) = 800 [円]

【別解】仕入れ値を □ 円とすると、A 商店、B 商店の定価はそれぞれ次のように表すことができる。
A：1.3 × □ [円]
B：1.25 × □ [円]
よって、次の式が成り立つ。
1.3 × □ – 1.25 × □ = 40
0.05 × □ = 40
□ = 800 [円]

問８

ある店で、ガラスのコップを 1 個 240 円で 500 個仕入れました。初日に 1 枚 300 円の定価をつけて売ったところ、380 個売れました。2 日目に、1 日目に売れ残った分を販売しようと点検を行った結果、8 分の 3 にあたる個数のコップにひびが入っていたことに気がついたため、ひびが入っていないコップのみ、定価の 16 % 引きで売ることにしました。なお、ひびの入ったコップは返品し、仕入れた金額と同額を返金してもらうことができました。

（１）初日の定価は、仕入れ値に何割何分の利益を見込んでつけた金額であるか求めなさい。

答え（１）

2 割 5 分

解き方（１）

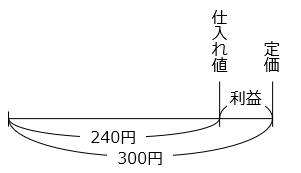
( 300 – 240 ) ÷ 240 = \(\dfrac{1}{4}\) = 0.25
より、2 割 5 分

（２）2 日目にひびが入っていないコップがすべて売り切れた場合の利益の総額を求めなさい。

答え（２）

23700 円

解き方（２）

初日の利益は、60 × 380 = 22800 [円]
2 日目にひびの入っていないコップの個数は、
( 500 – 380 ) × \(\dfrac{5}{8}\) = 75 [個]
より、2 日目の利益は、
300 × 0.84 × 75 – 240 × 75
= ( 252 – 240 ) × 75 = 900 [円]
割れたコップの利益は、仕入れ値と同額の返金があったので 0 円。
よって、利益の総額は、
22800 + 900 = 23700 [円]

（３）2 日目にひびが入っていないコップが何個か売れ残ってしまったので、3 日目は 2 日目の売り値の 6 円引きで売ったところ、全部売り切れ、利益の総額は 23610 円となりました。3 日目に売れたコップの個数を求めなさい。

答え（３）

15 個

解き方（３）

【つるかめ算を使う】
2 日目に全部売り切ってしまった場合の利益の総額は、（２）より 23700 円であるが、実際の利益の総額は 23610 円である。
よって、3 日目に 2 日目の売り値の 6 円引きで売れたコップの個数は、
( 23700 – 23610 ) ÷ 6 = 15 [個]

【別解①】面積図で考える
初日の利益は（２）より、22800 円より、2 日目と 3 日目の利益の合計は 23610 – 22800 = 810 [円]
2 日目に残っている割れていないコップは 75 個。2 日目のコップ 1 個の利益は 300 × 0.84 – 240 = 12 [円]、3 日目のコップ 1 個の利益は 12 – 6 = 6 [円] となる。

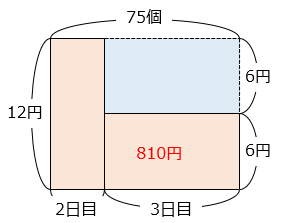
　 部分の面積は、2 日目と 3 日目の利益の合計より 810 円。
　 部分の面積は、75 × 12 – 810 = 90 円。
よって、3 日目に売れたコップの個数は、
90 ÷ 6 = 15 [個]

【別解②】消去算を使う
2 日目に売れた個数を A 個、3 日目に売れた個数を B 個とすると、以下の式が成り立つ。
A + B = 75 ・・・ ㋐
( 252 – 240 ) × A + ( 252 – 6 – 240 ) × B = 23610 – 22800
12 × A + 6 × B = 810
2 × A + B = 135 ・・・ ㋑
㋐ × 2 – ㋑ より、
B = 150 – 135 = 15 [個]

【別解③】式をつくる
3 日目に売れた個数を □ 個とすると、次の式が成り立つ。
12 × ( 75 – □ ) + 6 × □ = 810
( 12 – 6 ) × □ = 900 – 810
6 × □ = 90
□ = 15 [個]