算数【入試】倍数算
問1
A 子さんと B 子さんは同じ値段の消しゴムを買いに行きました。A 子さんと B 子さんの残金の比は、1 個ずつ買うと 13:21 になり、5 個ずつ買うと 3:5 になります。
(1)消しゴムを 7 個ずつ買ったときの A 子さんと B 子さんの残金の比を求めなさい。
- 答え(1)
- 23:39
- 解き方(1)
- 同じ個数を買うとき、残高の差は変わらないので、比の差をそろえる。
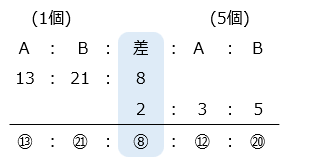
⑬ – ⑫ = ① が消しゴム 4 個分の値段の比を表す。消しゴムを 7 個ずつ買ったときの A 子さんと B 子さんの残金の比は、
( ⑫ – \(\dfrac{①}{4}\) × 2 ) : ( ⑳ – \(\dfrac{①}{4}\) × 2 ) = 23:39
(2)2 人がはじめに持っていたお金は合計で 7590 円でした。消しゴム 1 個の値段を求めなさい。
- 答え(2)
- 55 円
- 解き方(2)
- A 子さんと B 子さんがはじめに持っていたお金の比の合計は、
( ⑬ + \(\dfrac{①}{4}\) ) + ( ㉑ + \(\dfrac{①}{4}\) ) = \(\dfrac{138}{4}\)で、これが 7590 円に相当する。
よって、消しゴム 1 個の値段は、
\(\dfrac{①}{4}\) = 7590 ÷ 138 = 55 [円]
問2
はじめ A さんと B さんの所持金の比は 3:2 でした。A さんが B さんに 140 円わたすと 4:5 になりました。A さんのはじめの所持金は何円ですか。
- 答え
- 540 円
- 解き方
- 【和に注目して連比を考える】
やりとりの前後で 2 人の所持金の和は変わらないので、和に注目して連比を考える。
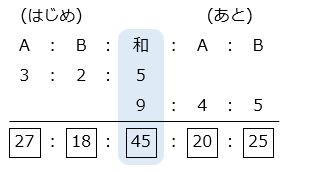
A さんはやりとりの前後で \(\boxed{27}\) – \(\boxed{20}\) = \(\boxed{7}\) 減っているので、\(\boxed{7}\) = 140 [円]、すなわち \(\boxed{1}\) = 20 [円]とわかる。A さんのはじめの所持金は \(\boxed{27}\) = 20 × 27 = 540 [円]
【「外項の積 = 内項の積」を利用する】
A さんのはじめの所持金を ③ とすると、B さんのはじめの所持金は ② となる。A さんが B さんに 140 円わたしたあとの比が 4:5 なので、
( ③ -140 ) : ( ② + 140 ) = 4:5
5 × ( ③ -140 ) = 4 × ( ② + 140 )
① = 180
よって、A さんのはじめの所持金は 3 × 180 = 540 [円]
問3
兄と弟の最初の所持金の比は 9:5 でした。その後、兄は靴を買い、弟は帽子を買いました。兄と弟の使った金額の比は 5:2 でした。残った金額は、兄が 1800 円、弟が 1700 円でした。
(1)弟が買った帽子はいくらでしたか。
- 答え(1)
- 1800 円
- 解き方(1)
- 【線分図を描いて考える】
兄の最初の所持金を ⑨ とすると、弟の最初の所持金は ⑤ となる。また、靴の金額を \(\boxed{5}\) とすると、帽子の金額は \(\boxed{2}\) となる。兄と弟の所持金の変化を線分図で表し、最初の所持金の比の大きさをそろえる。
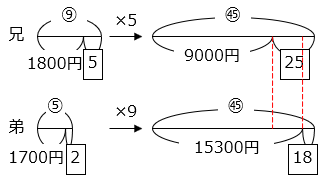
\(\boxed{25}\) – \(\boxed{18}\) = 15300 – 9000
\(\boxed{1}\) = 900
よって、帽子の金額は 900 × 2 = 1800 [円]
【「外項の積 = 内項の積」を利用する】
帽子の金額を ② とすると、靴の金額は ⑤ となる。兄と弟の最初の所持金はそれぞれ、⑤ + 1800、② + 1700 と表すことができ、その比が 9:5 である。よって、
⑤ + 1800:② + 1700 = 9:5
5 × ( ⑤ + 1800 ) = 9 × ( ② + 1700 )
① = 900
帽子の金額 ② は1800 円
(2)2 人の最初の所持金の合計金額はいくらでしたか。
- 答え(2)
- 9800 円
- 解き方(2)
- 弟の最初の所持金は、1800 + 1700 = 3500 [円] である。よって、2 人の最初の所持金の合計は、
3500 × \(\dfrac{14}{5}\) = 9800 [円]
問4
A さんと B さんの所持金の比は 5:1 でした。B さんは A さんから 750 円もらい、その後 B さんは 1100 円使いました。すると、A さんと B さんの所持金の比は 9:1 になりました。A さんははじめに何円持っていましたか。
- 答え
- 3000 円
- 解き方
- 【線分図を描いて考える】
A さんのはじめの所持金を ⑤ とすると、B さんの所持金は ① と表すことができる。A さんと B さんの所持金の変化を線分図で表し、最初の所持金の比の大きさをそろえる。
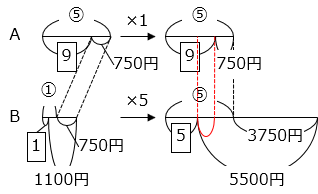
\(\boxed{9}\) – \(\boxed{5}\) = 5500 – 3750 – 750
\(\boxed{1}\) = 250
よって、A さんのはじめの所持金は 9 × 250 + 750 = 3000 [円]
【「外項の積 = 内項の積」を利用する】
A さんのはじめの所持金を ⑤ とすると、B さんの所持金は ① と表すことができる。B さんは A さんから 750 円もらい、その後 1100 円使ったので、A さんと B さんの所持金はそれぞれ ⑤ – 750、① – 350 となる。この比が 9:1 になることから、
⑤ – 750:① – 350 = 9:1
⑤ – 750 = 9 × ( ① – 350 )
① = 600 [円]
A さんのはじめの所持金は ⑤ なので、600 × 5 = 3000 [円]
問5
大人と子どもが何人かずついます。子どもには 1 人 4 個ずつ、大人には 1 人 3 個ずつあめを配ると、子どもと大人に配ったあめの数の合計の比は 2:1 になり、148 個余りました。そこで、子どもには 1 人 6 個ずつ、大人には 1 人 5 個ずつ配りなおすと、子どもと大人に配ったあめの合計の比は 9:5 になり、8 個余りました。子どもは何人いましたか。
- 答え
- 42 人
- 解き方
- 子どもと大人の人数の比は、\(\dfrac{2}{4}\):\(\dfrac{1}{3}\) = 3:2より、子どもの人数を ③ とすると、大人の人数は ② となる。よって、はじめに配ったあめの個数は、③ × 4 + ② × 3 = ⑱、あとに配った個数は ③ × 6 + ② × 5 = ㉘ となる。 あめの総数は変わらないので、
⑱ + 148 = ㉘ + 8
① = 14
子どもの人数は、3 × 14 = 42 [人]




