算数【応用】円とおうぎ形(角度・長さ・面積)
円周率は 3.14 とします。
問1
円周率とは、
\(\dfrac{\boxed{ア}\ の長さ}{\boxed{イ}\ の長さ}\)
のことです。\(\boxed{ア}\)、\(\boxed{イ}\) に当てはまる言葉の組み合わせを ① ~ ④ から選びなさい。
① ア:円の半径 イ:円周
② ア:円の直径 イ:円周
③ ア:円周 イ:円の半径
④ ア:円周 イ:円の直径
- 答え
- ④
問2
半径 6 cm の円の面積は、半径 9 cm で中心角が □° であるおうぎ形の面積と一致します。
□ に当てはまる数を答えなさい。
- 答え
- 160
- 解き方
- 半径 9 cm の円と半径 6 cm の円の半径と面積の関係を考える。
半径が \(\dfrac{2}{3}\) になると、面積は元の円の \(\dfrac{4}{9}\) になる。
よって、求める中心角は、
360 × \(\dfrac{4}{9}\) = 160 [°]
問3
半径 19.2 cm の円周の長さは、半径 9.2 cm の円周の長さより何 cm 長いですか。
- 答え
- 62.8 cm
- 解き方
- 19.2 × 2 × 3.14 – 9.2 × 2 × 3.14
= ( 38.4 – 18.4 ) × 3.14
= 20 × 3.14 = 62.8 [cm]
問4
半径 1 cm の 5 つの円が図のように重なっています。このとき、 部分の面積は何 cm2 ですか。
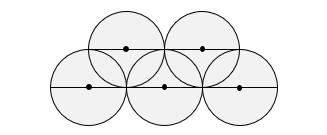
- 答え
- 13.42 cm2
- 解き方
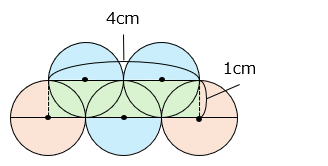
求める面積は、\(\dfrac{3}{4}\) 円( )が 2 つと半円( )が 3 つと長方形( )の和
また、\(\dfrac{3}{4}\) 円が 2 つと半円が 3 つは円 3 つと同じである。よって、
1 × 1 × 3.14 × 3 + 1 × 4
= 9.42 + 4 = 13.42 [cm2]
問5
中心が同じ 3 つの半円の弧にそって、図のように 4 cm 間隔で × 印をつけます。この印は最大で何個つけることができるか答えなさい。
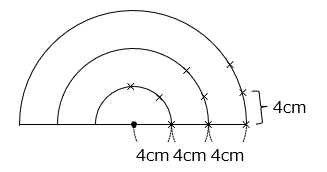
- 答え
- 21 個
- 解き方
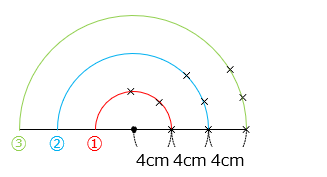
弧 ①、②、③ につけることのできる印の個数は、
① 4 × 2 × 3.14 ÷ 2 ÷ 4 = 3.14 ⇒ 4 個
① 8 × 2 × 3.14 ÷ 2 ÷ 4 = 6.28 ⇒ 7 個
① 12 × 2 × 3.14 ÷ 2 ÷ 4 = 9.42 ⇒ 10 個
よって、4 + 7 + 10 = 21 [個]
問6
図のように半径が 10 m で中心角が 90° のおうぎ形の中に半径が 5 m の半円が 2 つ入っています。このとき、 部分の面積は何 m2 ですか。
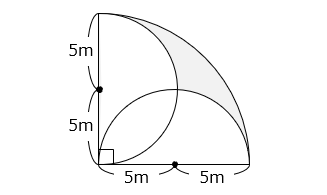
- 答え
- 14.25 m2
- 解き方
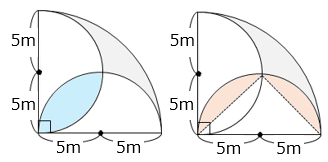
求める面積は、おうぎ形の面積から半円 2 つの面積を除き、 部分の面積を加えた面積となる。
おうぎ形の面積と半円 2 つの面積は等しいことから、求める面積は 部分の面積となる。
また、 部分の面積は 部分の面積と等しいので、求める面積は、
5 × 5 × 3.14 ÷ 2 – 10 × 5 ÷ 2
= 25 × 1.57 – 25
= 25 × ( 1.57 – 1 )
= 25 × 0.57 = 14.25 [m2]
※円の半径が \(\dfrac{1}{2}\) になると、面積は元の円の \(\dfrac{1}{4}\) になる。






