算数【応用】円を含む図形
円周率は 3.14 とします。
問1
図は、直角二等辺三角形 ABC と 2 つのおうぎ形を組み合わせたものです。点 M は辺 AC の中点です。 部分の面積は何 cm2 ですか。

- 答え
- 6.88 cm2
- 解き方
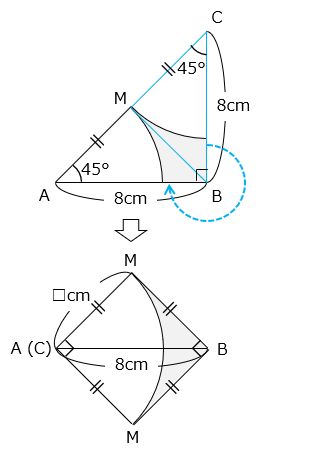
図の一部を動かすと、対角線が 8 cm の正方形の中に中心角が 90° のおうぎ形が収まっている。
対角線が 8 cm の正方形の面積は、
8 × 8 ÷ 2 = 32 [cm2]
よって、おうぎ形の半径を □ cm とすると、□ × □ = 32 と表すことができる。
おうぎ形部分の面積は、
□ × □ × 3.14 × \(\dfrac{90}{360}\)
= 32 × 3.14 × \(\dfrac{1}{4}\) = 25.12 [cm2]
したがって、 部分の面積は、
32 – 25.12 = 6.88 [cm2]
問2
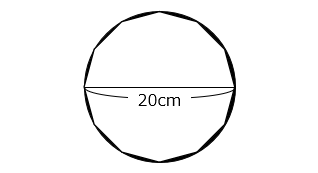
図は、正十二角形と、その頂点が通る円を表しています。このとき、 部分の面積の和は何 cm2 ですか。
- 答え
- 14 cm2
- 解き方

上図は正十二角形の一部です。図より、正十二角形の面積は、
( 10 × 5 ÷ 2 ) × 12 = 300 [cm2]
となる。よって、求める面積は、
10 × 10 × 3.14 – 300 = 14 [cm2]
問3
図は、1 辺の長さが 6 cm の正三角形と半円を組み合わせた図形です。 部分の面積は何 cm2 ですか。
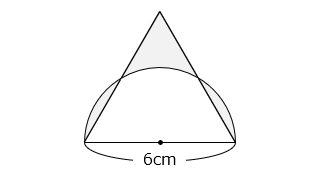
- 答え
- 4.71 cm2
- 解き方
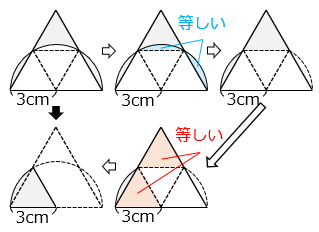
上図より、求める面積は面積は、半径 3 cm の中心角 60° のおうぎ形の面積と等しい。よって、
3 × 3 × 3.14 × \(\dfrac{60}{360}\) = 4.71 [cm2]
問4
図は、中心角が 90° のおうぎ形 OPQ と長方形 OABC を組み合わせたものです。 部分の面積が等しいとき、CQ の長さを求めなさい。ただし、円周率は 3.14 として、小数第 3 位を四捨五入して求めなさい。
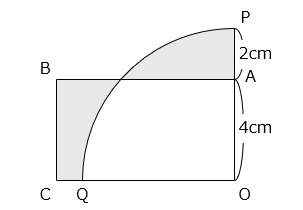
- 答え
- 1.07 cm
- 解き方
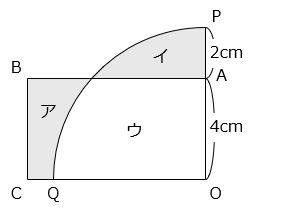
CQ の長さを □ cm とすると、
ア + ウ = 4 × ( 6 + □ ) = 24 + 4 × □
イ + ウ = 6 × 6 × 3.14 × \(\dfrac{90}{360}\) = 28.26
アとイの面積は等しいので、ア + ウ = イ + ウ が成り立つので、
24 + 4 × □ = 28.26
4 × □ = 28.26 – 24 = 4.26
□ = 1.065 ≒ 1.07 [cm]
問5
図のように、円の中に正方形がぴったり入っています。正方形の 1 辺の長さが 2 cm のとき、円の面積を求めなさい。
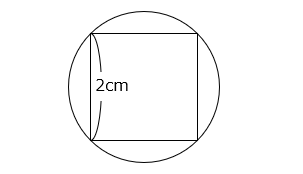
- 答え
- 6.28 cm2
- 解き方
- 円の半径を □ cm とすると、正方形の面積は次のように表すことができる。
( 2 × □ ) × ( 2 × □ ) ÷ 2 = 2 × □ × □
よって、次の式が成り立つ。
2 × □ × □ = 2 × 2 = 4
□ × □ = 2
円の面積は、
□ × □ × 3.14 = 2 × 3.14 = 6.28 [cm2]
【知っていると便利】
半径 × 半径 の値は、円に内接する正方形の面積の半分となる。
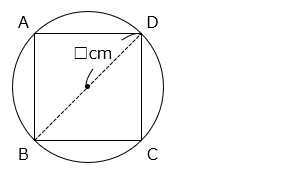
円の半径を □ cm とすると、この円に内接する正方形 ABCD の面積は、
正方形 ABCD = ( □ × 2 ) × ( □ × 2 ) ÷ 2
正方形 ABCD = □ × □ × 2
□ × □ = 正方形 ABCD ÷ 2
問6
図のように、大、中、小の 3 つの円と、一辺の長さが 1 cm の正方形が 9 個あります。大、中、小の 3 つの円の中心はそれぞれ点 A、点 B、点 C で、半径はそれぞれ 3 cm、2 cm、1 cm です。 部分の面積を答えなさい。
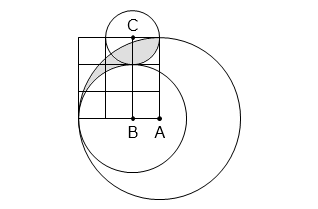
- 答え
- 1.71 cm2
- 解き方
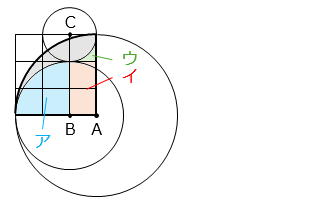
上図より、求める面積は半径 3 cm のおうぎ形の面積から、ア、イ、ウの面積を除いた部分である。
ア = 2 × 2 × 3.14 × \(\dfrac{90}{360}\) = 3.14 [cm2]
イ = 1 × 2 = 2 [cm2]
ウ = 1 × 1 – 1 × 1 × 3.14 × \(\dfrac{90}{360}\) = 1 – 3.14 × \(\dfrac{1}{4}\) [cm2]
ア + イ + ウ = 3.14 + 2 + 1 – 3.14 × \(\dfrac{1}{4}\) = 3 + 3.14 × \(\dfrac{3}{4}\)
よって、求める面積は、
3 × 3 × 3.14 × \(\dfrac{1}{4}\) – ( 3 + 3.14 × \(\dfrac{3}{4}\) )
= 3.14 × \(\dfrac{9}{4}\) – 3 – 3.14 × \(\dfrac{3}{4}\)
= 3.14 × ( \(\dfrac{9}{4}\) – \(\dfrac{3}{4}\) ) – 3
= 3.14 × \(\dfrac{3}{2}\) – 3
= 1.57 × 3 – 3
= 3 × ( 1.57 – 1 ) = 3 × 0.57 = 1.71 [cm2]
問7
四角形 ABCD は正方形、三角形 ADE は AD = DE の二等辺三角形、曲線は円の一部です。ア、イの角度を求めなさい。
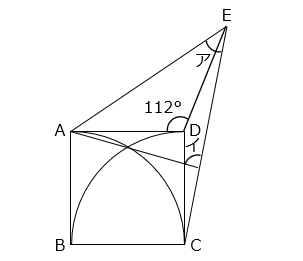
- 答え
- ア:45° イ:86°
- 解き方
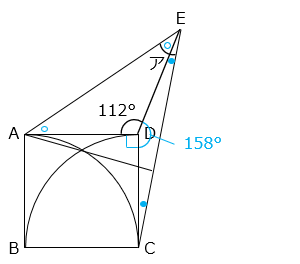
上図より、ア = ○ + ● と表すことができる。
△ADE は二等辺三角形より、
○ = ( 180 – 112 ) ÷ 2 = 34 [°]
角 CDE = 360 – 112 – 90 = 158 [°]、また、△CDE は CD = DE の二等辺三角形より、
● = ( 180 – 158 ) ÷ 2 = 11 [°]
よって、ア = 34 + 11 = 45 [°]
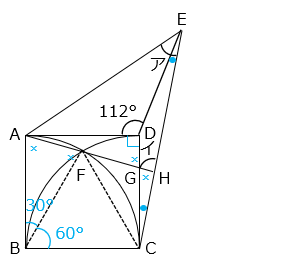
上図のように点 F、G、H をとる。
△ BFC は正三角形、△ ABF は AB = BF の二等辺三角形より、
× = ( 180 – 30 ) ÷ 2 = 75 [°]
角 BAG と角 AGD は錯角、角 AGD と 角 CGH は対頂角の関係より、
角 BAG = 角 AGD = 角 CGH = ×
イ = ● + × = 11 + 75 = 86 [°]
問8
図は長方形と \(\dfrac{1}{4}\) 円を組み合わせたものです。角アの大きさは何度ですか。
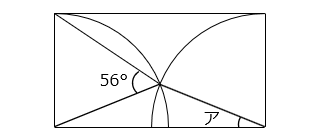
- 答え
- 22 度
- 解き方
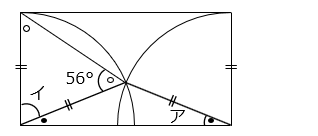
イ = 180 – 56 × 2 = 68 [°]
ア = ● = 90 – イ = 90 – 68 = 22 [°]
問9
図は正方形と半円、\(\dfrac{1}{4}\) 円を組み合わせたものです。 部分の面積は何 cm ですか。
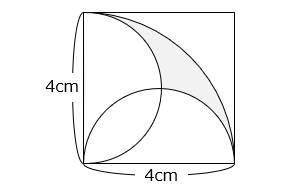
- 答え
- 2.28 cm2
- 解き方
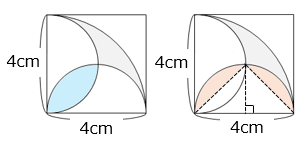
部分の面積は、\(\dfrac{1}{4}\) 円から 2 つの半円の面積を除き、 部分の面積を加えた面積となる。
\(\dfrac{1}{4}\) 円と 2 つの半円の面積の和は等しいことから、 部分の面積は 部分の面積に等しい。
また、 部分と 部分の面積は等しくなる。
よって、求める面積は、
2 × 2 × 3.14 × \(\dfrac{1}{2}\) – 4 × 2 × \(\dfrac{1}{2}\)
= 6.28 – 4 = 2.28 [cm2]
※円の半径と面積の関係
半径が \(\dfrac{1}{2}\) になると、面積は \(\dfrac{1}{4}\) になる。
問10
図のように、1 辺の長さが 1 cm の正方形を 16 個組み合わせました。曲線は半径が 1 cm または 3 cm の円の一部です。 部分の面積は何 cm2 ですか。
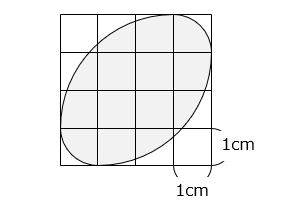
- 答え
- 11.7 cm2
- 解き方
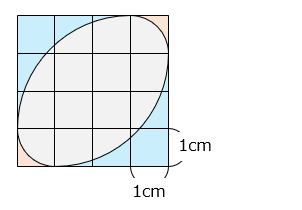
求める面積は、1 辺の長さが 4 cm の正方形から、 部分と 部分の面積を除くと求められる。
部分の面積は、
( 3 × 3 – 3 × 3 × 3.14 × \(\dfrac{1}{4}\) ) × 2
= ( 9 – 7.065 ) × 2 = 3.87 [cm2]
部分の面積は、
( 1 × 1 – 1 × 1 × 3.14 × \(\dfrac{1}{4}\) ) × 2
= ( 1 – 0.785 ) × 2 = 0.43 [cm2]
求める面積は、
4 × 4 – 3.87 – 0.43 = 11.7 [cm2]
問11
図のように半径 3 cm の半円に長方形がちょうど入っています。 部分の面積は何 cm2 ですか。
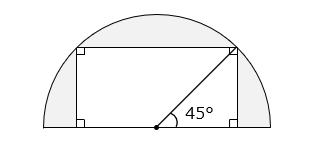
- 答え
- 5.13 cm2
- 解き方
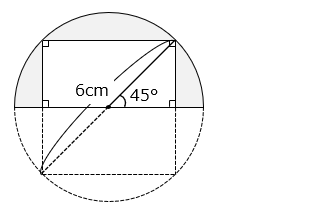
長方形の面積は、半径 3 cm の円にちょうど入っている正方形の面積の半分である。よって、長方形の面積は、
6 × 6 ÷ 2 ÷ 2 = 9 [cm2]
よって、求める面積は、
3 × 3 × 3.14 ÷ 2 – 9
= 9 × 1.57 – 9
= 9 × ( 1.57 – 1 )
= 9 × 0.57 = 5.13 [cm2]























