算数【応用】速さ・時間・道のり
問1
A さんは、公園で友達と待ち合わせの約束をしました。家を出て、毎分 60 m の速さで歩くと約束の時間よりも 5 分早く公園に着き、毎分 40 m の速さで歩くと約束の時間よりも 3 分おくれて公園に着きます。家から公園までの道のりは何 m ですか。
- 答え
- 960 m
- 解き方
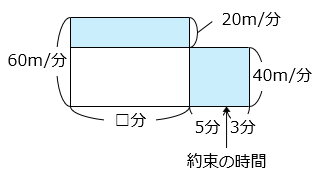
60 m/分で公園に着くまでにかかる時間を□分とする。
20 × □ = 40 × ( 5 + 3 ) = 320
□ = 16 [分]
よって、公園までの道のりは、
60 × 16 = 960 [m]
問2
A さんは P 町から Q 町までは毎時 6 km で走り、Q 町から R 町までは自転車に乗って毎時 14 km で進んだところ、全部で 3 時間 30 分かかりました。P 町から R 町までの道のりが 23 km のとき、P 町から Q 町までの道のりは何 km ですか。
- 答え
- 19.5 km
- 解き方
- 3 時間 30 分は ( 3 × 60 + 30 ) ÷ 60 = \(\dfrac{210}{60}\) = \(\dfrac{7}{2}\) [時間]
P 町から Q 町までの道のりを□ km とし、かかった時間に注目すると、以下の式が成り立つ。
\(\dfrac{□}{6}\) + \(\dfrac{23\ -\ □}{14}\) = \(\dfrac{7}{2}\)
7 × □ + 3 × ( 23 – □ ) = 21 × 7
7 × □ – 3 × □ = 3 × 7 × 7 – 3 × 23
4 × □ = 3 × ( 49 – 23 ) = 78
□ = 19.5 [km]
問3
A さんの家と駅の距離は 3 km です。
A さんは、駅を 9 時 50 分に出発する電車に乗るために、家を 9 時ちょうどに出発して分速 60 m で歩き始めました。1.8 km の地点で友達の B さんに出会ったので立ち止まって 10 分間おしゃべりをしました。その後、駅に向かって分速 110 m で走りました。
(1)A さんが B さんに出会ったのは家を出発してから何分後ですか。
- 答え(1)
- 30 分後
- 解き方(1)
- ( 1.8 × 1000 ) ÷ 60 = 30 [分後]
(2)A さんは駅を 9 時 50 分に出発する電車に間に合いましたか。
間に合った場合は解答欄に「間に合った」と書きなさい。
間に合わなかった場合は、間に合うためには分速何 m 以上で走ればよかったのかを求めて、分速を答えなさい。
- 答え(2)
- 分速 120 m
- 解き方(2)
- B さんに出会うまでに 30 分かかり、10 分間おしゃべりしていたので、残りの時間は 50 – 30 – 10 = 10 [分]
10 分以内に駅に着けば間に合う。
B さんに出会った地点から駅までの距離は 3 – 1.8 = 1.2 [km] より、分速 110 m で走ったときにかかる時間は、
( 1.2 × 1000 ) ÷ 110 = 10.9 … > 10 ⇒ 間に合わない
間に合うための最低の速度は、
1200 ÷ 10 = 120 [m/分]
問4
池の周りを、1 周目は時速 4.5 km で、2 周目は時速 10 km で進み、4 分休憩してから 3 周目は時速 15 km で進んだところ、ちょうど 1 時間かかりました。池の周りは 1 周何 m ですか。
- 答え
- 2400 m
- 解き方
- 休憩時間を除くと、( 60 – 4 ) ÷ 60 = \(\dfrac{56}{60}\) = \(\dfrac{14}{15}\) [時間]
1 周を□ km として、かかった時間に注目すると、以下の式が成り立つ。
\(\dfrac{□}{4.5}\) + \(\dfrac{□}{10}\) + \(\dfrac{□}{15}\) = \(\dfrac{14}{15}\)
20 × □ + 9 × □ + 6 × □ = 6 × 14
35 × □ = 84
□ = \(\dfrac{12}{5}\) = 2.4 [km] = 2400 [m]
問5
A さんの家から学校までは 2.1 km あります。A さんは午前 7 時 30 分に家を出発して、毎分 70 m の速さで学校に向かいました。途中で忘れ物に気がついて、毎分 140 m の速さで家に引き返しました。忘れ物を見つけるまでに 1 分かかり、再び毎分 70 m の速さで学校に向かったところ、午前 8 時 10 分に学校に着きました。忘れ物に気がついて引き返したのは家から何 m 進んだ地点ですか。
- 答え
- 420 m
- 解き方
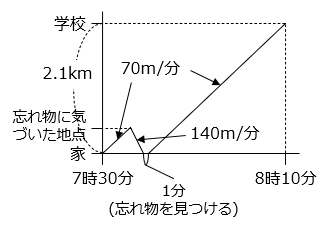
学校に着くまでにかかった時間は全体で 40 分。
毎分 70 m で家から学校に着くまでにかかる時間は ( 2.1 × 1000 ) ÷ 70 = 30 [分]
したがって、家と忘れ物をした地点を往復するのにかかった時間は、
40 – 30 – 1 = 9 [分]
家から忘れ物をした地点までの距離を□ m とし、かかった時間に注目すると、以下の式が成り立つ。
\(\dfrac{□}{70}\) + \(\dfrac{□}{140}\) = 9
2 × □ + □ = 1260
□ = 1260 ÷ 3 = 420 [m]
問6
駅から学校に向かうため、A さんは分速 150 m で歩き、B さんは時速 45 km で進むバスに乗りました。B さんの乗ったバスは、途中にある 3 つの信号で、それぞれ 2 分ずつ停車しました。2 人は同時に出発しましたが、A さんは B さんよりも 10 分遅れて学校に到着しました。駅から学校までの道のりは何 km ですか。
- 答え
- 3 km
- 解き方
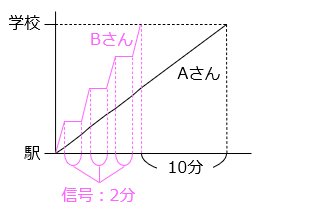
B さんの乗ったバスが信号で止まらなかったとすると、A さんよりも 16 分早く学校に着く。
時速 45 km を分速に変換すると、
( 45 × 1000 ) ÷ 60 = 750 [m/分]
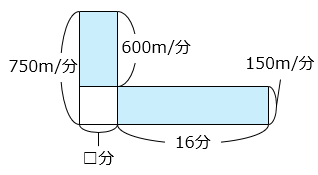
信号で止まった時間を除いた時間を□分とすると、
600 × □ = 150 × 16 = 2400
□ = 4 [分]
よって、駅から学校までの道のりは、
750 × 4 = 3000 [m] = 3 [km]
問7
A さんは 8 時 30 分に家を出て 6 km 離れた公園に行きました。A さんは毎時 3.6 km の速さで歩き、15 分間歩くごとに 3 分間休みました。
(1) A さんは公園に着くまでに何回休みましたか。
- 答え(1)
- 6 回
- 解き方(1)
- A さんが 15分で進む距離は 3.6 × \(\dfrac{15}{60}\) = 0.9 [km]
6 ÷ 0.9 = 6 あまり 0.6
よって、6 回
(2) A さんは何時何分に公園に着きましたか。
- 答え(2)
- 10 時 28 分
- 解き方(2)
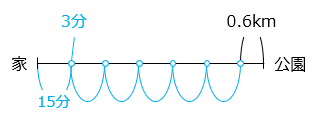
最後に休んだのは公園から 0.6 km の地点より、家から公園に着くまでにかかった時間は、
15 × 6 + 3 × 6 + 0.6 ÷ 3.6 × 60
= 90 + 18 + 10 = 118 [分] = 1 時間 58 分
よって、公園に着いたのは 8 時 30 分から 1 時間 58 分後 より、10 時 28 分





