算数【入試】速さ・時間・道のり

問１

3 km の道のりを進むのに 36 分かかりました。進む速さは時速何 km ですか。

答え: 時速 5 km

解き方: 36 分 = 0.6 時間
3 ÷ 0.6 = 5 [km/時]

問２

周囲が 2.7 km の池の周りを A 君と B 君が逆向きに歩きます。A 君の速さは分速 60 mとします。2 人が同時に歩き始めてから出会うまでに 18 分かかりました。B 君の速さは分速何 m ですか。

答え: 分速 90 m

解き方: A 君が 18 分間で進んだ道のりは 60 × 18 = 1080 [m]
B 君が 18 分間で進んだ道のりは 2.7 × 1000 – 1080 = 1620 [m] より、
1620 ÷ 18 = 90 [m/分]

【別解】出会い算として考える
B 君の速さを分速 □ m とすると、次の式が成り立つ。
( □ + 60 ) × 18 = 2700
□ + 60 = 2700 ÷ 18 = 150
□ = 150 – 60 = 90 [m/分]

問３

A 市から B 市まで、電車では 2 時間 48 分、バスでは 3 時間 30 分かかります。電車の速さはバスの速さの何倍ですか。

答え: 1.25 倍

解き方: 2 時間 48 分 = 168 分
3 時間 30 分 = 210 分
同じ距離を移動するとき、速さの比はかかる時間の比の逆比となる。
よって、電車とバスの速さを比で表すと、電車：バス = 210：168 = 5：4
電車の速さはバスの \(\dfrac{5}{4}\) = 1.25 [倍] となる。

問４

自転車で 18 分の道のりを、歩くと 54 分かかります。その道のりを、A 君が歩いて出発してから 20 分後に、B 君は自転車で出発しました。B 君が A 君に追いつくのは、B 君が出発して何分後ですか。

答え: 10 分後

解き方: 同じ距離を移動するとき、速さの比はかかる時間の比の逆比となる。
よって、自転車の速さと歩く速さを比で表すと、
自転車：歩く = 54：18 = 3：1
となる。
追いかけ算として考える。
A 君の歩く速さを ① とすると、B 君が自転車で移動する速さは ③ とあらわすことができる。
B 君が A 君に追いつくのは、
( ① × 20 ) ÷ ( ③ – ① )
= ⑳ ÷ ② = 10 [分後]

問５

A 君は家から 6 km 離れた図書館へ時速 4.8 km で歩いて向かいました。出発して 30 分後に一度休んで、その後も休む前と同じ速さで歩き、家を出発してから 1 時間 20 分後に図書館に到着しました。A 君が出発した 41 分後に、B 君は時速 12 km で自転車に乗って図書館に向かいました。

（１）A 君は何分間休みましたか。

答え（１）: 5 分間

解き方（１）: 休まずに図書館に向かった場合にかかる時間は、
6 ÷ 4.8 = \(1\dfrac{1}{4}\) [時間] ⇒ 1 時間 15 分
よって、休んだのは 5 分間

（２）B 君が A 君に追いつくのは、B 君が出発して何分後ですか。

答え（２）: 24 分後

解き方（２）: A 君が出発した 41 分後、A 君が家から進んだ距離は、
4.8 × { ( 41 – 5 ) ÷ 60 }
= 4.8 × ( 36 ÷ 60 ) = 2.88 [km]
追いかけ算として考えると、B 君が A 君に追いつくのは、
2.88 ÷ ( 12 – 4.8 )
= 2.88 ÷ 7.2 = 0.4 [時間後] ⇒ 24 分後

問６

A 君は校庭を毎分 130 m の速さで 10 分間走りました。B 君は同じ 10 分間で A 君より 200 m 長く走りました。B 君は毎分何 m の速さで走りましたか。

答え: 毎分 150 m

解き方: ( 130 × 10 + 200 ) ÷ 10 = 150 [m/分]

問７

秒速 80 cmと時速 2.4 kmの合計の速さは分速 32 mの何倍の速さですか。

答え: \(2\dfrac{3}{4}\) 倍

解き方: 速さの単位を [m/分] にそろえる。
秒速 80 cm ⇒ \(\dfrac{80}{100}\) ÷ \(\dfrac{1}{60}\) = 48 [m/分]
時速 2.4 km ⇒ ( 2.4 × 1000 ) ÷ ( 1 × 60 ) = 40 [m/分]
これらの合計の速さは 48 + 40 = 88 [m/分] より、
88 ÷ 32 = \(\dfrac{11}{4}\) = \(2\dfrac{3}{4}\) [倍]

問８

15 km の道のりを行きは毎時 4 km、帰りは毎時 6 km の速さで歩くと、往復で何時間何分かかりますか。

答え: 6 時間 15 分

解き方: 15 ÷ 4 + 15 ÷ 6
= 3.75 + 2.5 = 6.25 [時間] ⇒ 6 時間 15 分

問９

縮尺 \(\dfrac{1}{15000}\) の地図があります。この地図上で 36 cm の道のりを、実際に自動車が一定の速さで走ったところ、6 分 45 秒かかりました。この自動車の速さは毎時何 km ですか。

答え: 毎時 48 km

解き方: 実際の距離は、
36 ÷ 100000 × 15000
= \(\dfrac{36\ ×\ 15}{100}\) = \(\dfrac{27}{5}\) [km]
6 分 45 秒 ⇒ 6 ÷ 60 + 45 ÷ 60 ÷ 60 = \(\dfrac{1}{10}\) + \(\dfrac{1}{80}\) = \(\dfrac{9}{80}\) [時間]
この自動車の速さは、
\(\dfrac{27}{5}\) ÷ \(\dfrac{9}{80}\)
= \(\dfrac{\cancelto{3}{27}}{\cancel{5}}\) × \(\dfrac{\cancelto{16}{80}}{\cancel{9}}\) = 48 [km/時]

問１０

はなこさんは家を出発して一人で学校まで歩いて向かっていました。途中でめぐみさんと出会い、二人で歩いて行ったところ、一人で行くより 3 分遅く到着しました。一人で歩く速さは毎分 60 m、二人で歩く速さは毎分 45 m とします。

（１）二人で歩いた時間は何分ですか。

答え（１）: 12 分

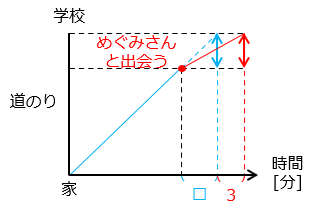
解き方（１）: めぐみさんと出会った地点から学校まで、一人で歩くときと同じ速さで進んだ場合にかかる時間を□ [分] として考える。

【面積図で考えてみると】
めぐみさんと出会った地点から学校までの道のりを考える。たてを速さ、横を時間とすると、面積が道のりとなる。

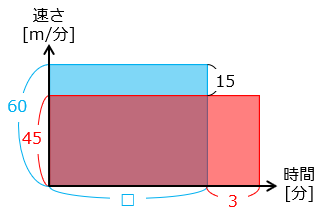
　と　の面積は、めぐみさんと出会った地点から学校までの道のりを表している。重なった部分を除いた面積は等しくなるので、
( 60 – 45 ) × □ = 45 × 3
15 × □ = 135
□ = 9 [分]
よって、二人で歩いた時間は、9 + 3 = 12 [分]

【別解　式で考えてみると】
二人で歩いた時間は □ + 3 [分] と表すことができる。
歩いた道のりは等しいので、
60 × □ = 45 × ( □ + 3 )
□ = 9 [分]
よって、二人で歩いた時間は 9 + 3 = 12 [分]

（２）家から学校までの道のりの半分を一人で、残りの半分を二人で歩いて行くと、一人で行くより 10 分遅く到着します。このとき、家から学校までの道のりは何 km ですか。

答え（２）: 3.6 km

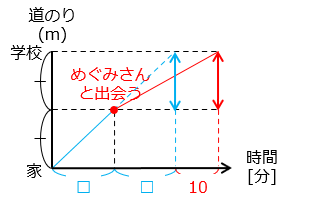
解き方（２）: 家からめぐみさんと出会うまでの時間を □ [分] として考える。

【面積図で考えてみると】
たてを速さ、横を時間とすると、面積が道のりとなる。
めぐみさんと出会った地点は学校まで半分の道のりである。よって、一人で歩くときと同じ速さで歩くと、めぐみさんと出会った地点から学校までかかる時間も □ [分] となる。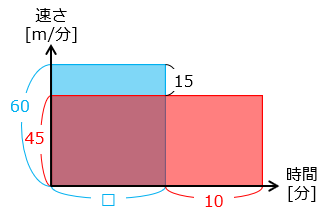
　と　の面積は、めぐみさんと出会った地点から学校までの道のりを表している。重なった部分を除いた面積は等しくなるので、
( 60 – 45 ) × □ = 45 × 10
15 × □ = 450
□ = 30 [分]
よって、はなこさんは家から学校まで毎分 60 m で 60 分かかる。
家から学校までの道のりは、
60 × 60 = 3600 [m\\] = 3.6 [km]

【別解　式で考えてみると】
二人で歩いた時間は □ + 10 [分] と表すことができる。
歩いた道のりは等しいので、
60 × □ = 45 × ( □ + 10 )
15 × □ = 450
□ = 30 [分]
よって、家から学校までの道のりは、60 × 30 × 2 = 3600 [m] = 3.6 [km]