算数【基本】平均

平均

●式で表す
平均 = 合計 ÷ 個数
⇔ 合計 = 平均 × 個数
⇔ 個数 = 合計 ÷ 平均

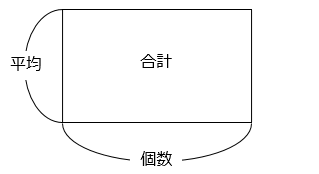
●面積図
「合計 = 平均 × 個数」は図のような面積で表すことができる


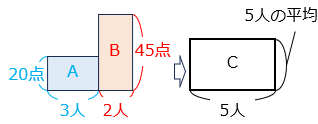
例）3 人の得点の平均が 20 点、2 人の得点の平均が 45 点のとき
3 人の得点の合計 = 面積 A
2 人の得点の合計 = 面積 B
5 人の得点の合計 = 面積 C

より、A + B = C　となる。
したがって、2つの面積図を重ねると、

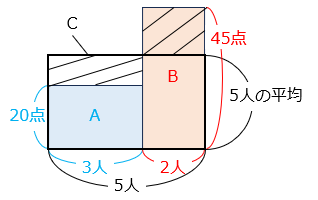
斜線部の面積は等しくなる。

問１

（１）あるクラスで算数のテストを行ったところ、男子 25 人の平均点は 72 点、女子 20 人の平均点は 81 点でした。このクラス全体の平均点は何点ですか。

答え（１）

76 点

解き方（１）

男子25人の合計点は 25 × 72 = 1800 [点]
女子 20 人の合計点は 20 × 81 = 1620 [点]
よって、クラス全体の平均点は、
( 1800 + 1620 ) ÷ ( 25 + 20 )
= 3420 ÷ 45 = 76 [点]

（２）グループ A とグループ B に同じ算数のテストをしました。グループ A は 10 人で平均点は 70.5 点、グループ B の平均点は 83 点です。また 2 つのグループを合わせた平均点は 78 点です。グループ B の人数は何人ですか。

答え（２）

15 人

解き方（２）

グループ B の人数を □ 人として面積図をかく。

斜線部の面積が等しくなることから、
5 × □ = 7.5 × 10 = 75
□ = 15 [人]

（３）A さんは、100 点満点のテストを 4 回受けました。1 回目と 2 回目は同じ点数で、3 回目は 61 点、4 回目は 87 点、4 回目までの平均点は 75 点でした。1 回目の得点は何点ですか。

答え（３）

76点

解き方（３）

1 回目の得点を □ 点とすると、2 回目の得点も □ 点となる。よって、
2 × □ + 61 + 87 = 75 × 4
2 × □ + 148 = 300
2 × □ = 300 – 148 = 152
□ = 76 [点]

（４）国語、算数、理科、社会の 4 つのテストをしました。算数以外の 3 つの平均点は 64 点でした。4 つのテストの平均点を70 点以上にするには、算数を何点以上とればよいですか。

答え（４）

88点

解き方（４）

平均点が 70点 のとき、算数を □ 点とすると、
64 × 3 + □ = 70 × 4
192 + □ = 280
□ = 280 – 192 = 88 [点]
平均点が 70 点以上になるのは、算数が 88 点以上のとき

【別解】面積図をかく

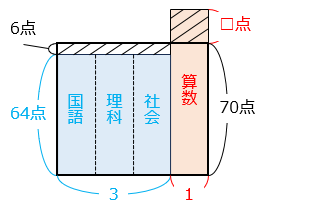
4 つのテストの平均点が 70 点のとき、算数の点数が 4 つのテストの平均より □ 点高いとする。
斜線部の面積は等しいので、次の式が成り立つ。
1 × □ = 3 × 6
□ = 18 [点]
よって、平均点が 70 点以上になるのは、算数が 70 + 18 = 88 [点] 以上のとき

（５）A さんの第 1 回から第 □ 回までのテストの平均点は 72 点です。次のテストで 100 点をとると、平均点は 74 点になります。□ に当てはまる数を答えなさい。

答え（５）

13

解き方（５）

面積図をかく。

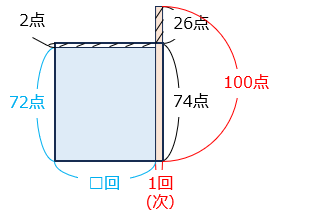
斜線部の面積が等しくなるので、
2 × □ = 26 × 1
□ = 13 [回]

（６）男子生徒 60 人と女子生徒 40 人が、算数のテストを受けました。100 人全員の平均点が 72.2 点で、男子生徒の平均点が 71 点でした。女子生徒の平均点は何点でしたか。

答え（６）

74 点

解き方（６）

全員の合計点は 100 × 72.2 = 7220 [点]、男子の合計点は 71 × 60 = 4260 [点] より、女子の合計点は、
7220 – 4260 = 2960 [点]
よって女子の平均点は、
2960 ÷ 40 = 74 [点]

【別解】面積図をかく。

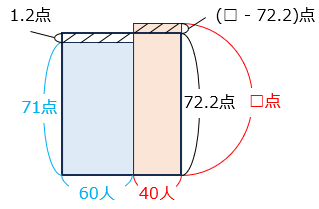
斜線部の面積が等しくなるので、
( □ – 72.2 ) × 40 = 1.2 × 60
40 × □ – 2888 = 72
40 × □ = 72 + 2888 = 2960
□ = 2960 ÷ 40 = 74 [点]

（７）男子が 30 人、女子が 20 人いるクラスで算数のテストを行ったところ、男子の平均点は女子より 5 点低く、男女全体の平均点は 72 点でした。このとき、男子の平均点は何点ですか。

答え（７）

70 点

解き方（７）

男子の平均点を □ 点とすると、女子の平均点は ( □ + 5 ) 点となる。
全員の合計点は 50 × 72 = 3600 [点] より、
30 × □ + 20 × ( □ + 5 ) = 3600
30 × □ + 20 × □ + 100 = 3600
30 × □ + 20 × □ = 3600 – 100
50 × □ = 3500
□ = 70 [点]

問２

（１）算数のテストについて、次のことがわかっています。

① A、B、C 3 人の平均点は72点です。

② C、D 2 人の平均点は60点です。

③ A、B、D 3 人の合計点は264点です。

このとき、A、B、C、D 4 人の平均点は何点ですか。

答え（１）

75 点

解き方（１）

A、B、C、D それぞれの点数を A 点、B 点、C 点、D 点とする。
①より、A + B + C = 72 × 3 = 216 ・・・(1)
②より、C + D = 60 × 2 = 120 ・・・(2)
③より、A + B + D = 261 ・・・(3)
(1) + (3) – (2)より、
A + B + C + A + B + D – ( C + D ) = 216 + 264 – 120
2 × A + 2 × B + ( C + D ) – ( C + D ) = 360
2 × ( A + B ) = 360
A + B = 180 ・・・(4)
4人の平均点は ( A + B + C + D ) ÷ 4 より、(2)+(4)より、
( A + B + C + D ) ÷ 4
= ( 180 + 120 ) ÷ 4
= 300 ÷ 4 = 75 [点]

（２）A、B、C 3人の平均点は A、B、C、D、E 5 人の平均点より 9 点低くなっています。D、E 2 人の合計点は 163 点でした。このとき 5 人の平均点は何点ですか。

答え（２）

68 点

解き方（２）

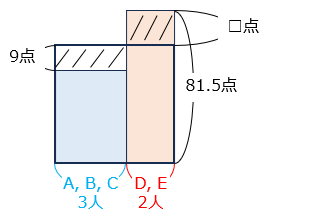
面積図より、斜線のところが同じ面積になるので、
ABC の 3 人分の面積は、3 × 9 = 27
DE の 2 人の平均は、27 ÷ 2 = 13.5 [点] 高い
DE の平均は、163 ÷ 2 = 81.5 [点] なので、
5 人の平均は、81.5 – 13.5 = 68 [点]

【別解】式で解く
A、B、C、D、E それぞれの点数を A 点、B 点、C 点、D 点、E 点とする。
「A、B、C 3 人の平均点は A、B、C、D、E 5 人の平均点より 9 点低い」より、
( A + B + C ) ÷ 3 = { ( A + B + C + D + E ) ÷ 5 } – 9
{ ( A + B + C ) ÷ 3 } × 15 = [ { ( A + B + C + D + E ) ÷ 5 } – 9 ] × 15
5 × ( A + B + C ) = 3 × ( A + B + C + D + E ) – 135
2 × ( A + B + C ) = 3 × ( D + E ) – 135 ・・・①
「D、E 2 人の合計点は 163 点」より、
D + E = 163 ・・・②
①を②で置き換えると、
2 × ( A + B + C ) = 3 × 163 – 135 = 354
A + B + C = 177 ・・・③
5人の平均点は ( A + B + C + D + E ) ÷ 5 より、②③で置き換えて計算すると、
( A + B + C + D + E ) ÷ 5
= ( 177 + 163 ) ÷ 5
= 340 ÷ 5 = 68 [点]

（３）4 人のうち、3 人ずつの得点の平均は 68 点、75 点、67 点、84 点でした。4 人の得点の平均は何点ですか。

答え（３）

73.5 点

解き方（３）

4 人を A、B、C、D すると、3 人ずつの組み合わせは、( A, B, C )、 (A, B, D )、( A, C, D )、( B, C, D ) となる。よって、A、B、C、D の得点を A 点、B 点、C 点、D 点とすると、
3 × ( A + B + C + D ) = 3 × ( 68 + 75 + 67 + 84 )
A + B + C + D = 68 + 75 + 67 + 84 = 294
4 人の得点の平均は 294 ÷ 4 = 73.5 [点]

問３

（１）グラフは、30 人のクラスで行った 10 点満点のテストの点数の記録です。全体の平均点は何点ですか。

答え（１）

6.1 点

解き方（１）

( 1 × 0 + 2 × 1 + 3 × 2 + 4 × 2 + 5 × 9 + 6 × 3 + 7 × 5 + 8 × 4 + 9 × 3 + 10 × 1 ) ÷ 30
= ( 0 + 2 + 6 + 8 + 45 + 18 + 35 + 32 + 27 + 10 ) ÷ 30
= 183 ÷ 30 = 6.1 [点]

（２）30 人のクラスで 5 点満点の算数のテストをしました。グラフはそのテストの結果を表したものです。テストの平均点は 3.6 点で、グラフは 3 点と 4 点のところがまだ完成していません。3 点と 4 点をとった人はそれぞれ何人ですか。

答え（２）

3 点：8 人　4点：9 人

解き方（２）

3 点をとった人数を A 人、4 点をとった人数を B 人とする。
全員で 30 人より、
2 + 3 + A + B + 8 = 30
A + B = 17 ・・・①
全員の合計点は 3.6 × 30 = 108 より、
1 × 2 + 2 × 3 + 3 × A + 4 × B + 5 × 8 = 108
2 + 6 + 3 × A + 4 × B + 40 = 108
3 × A + 4 × B = 60 ・・・②
① × 4 – ②より、
A = 17 × 4 – 60 = 8(人) ・・・③
①より、
8 + B = 17
B = 9 [人]

（３）表はあるクラスで 5 点満点のテストを行った結果をまとめたものです。このクラスの人数は 30 人、平均点は 3.4 点でした。このとき、A と B に入る数字をそれぞれ答えなさい。

答え（３）

A：2　B：7

解き方（３）

クラスの人数は30人より、
1 + 2 + A + 11 + B + 7 = 30
A + B = 9 ・・・①
合計点は 3.4 × 30 = 102 より、
0 × 1 + 1 × 2 + 2 × A + 3 × 11 + 4 × B + 5 × 7 = 102
0 + 2 + 2 × A + 33 + 4 × B + 35 = 102
2 × A + 4 × B = 32
A + 2 × B = 16 ・・・②
② – ①より、
B = 16 – 9 = 7 [人] ・・・③
①より、
A + 7 = 9
A = 2 [人]

（４）次の内容は、A さんが算数のテストを 7 回受けたときのものです。1 回目、3 回目、6 回目の得点は表の通りです。

㋐ 1 回目から 2 回目、2 回目から 3 回目は同じ点数ずつ得点が増えた。

㋑ 5 回目から 6 回目、6 回目から 7 回目は同じ点数ずつ得点が減った。

㋒ 4 回目のテストの得点は 2 回目と 6 回目の得点の間にあり、7 回のテストの平均点は整数で表すことができた。

① 2 回目の得点を求めなさい。

答え（４）- ①

64 点

解き方（４）- ①

㋐より、2 回目の得点は、
57 + ( 71 – 57) ÷ 2
= 57 + 14 ÷ 2 = 64 [点]

② 4 回目の得点を求めなさい。

答え（４）- ②

67 点

解き方（４）- ②

㋐より、1 ～ 3 回目の合計点は 64 × 3 = 192 [点]
㋑より、5 ～ 7 回目の合計点は 70 × 3 = 210 [点]
よって、4 回目の得点を □ 点とすると、1 ～ 7 回目の合計点は ( 192 + □ + 210 ) 点と表すことができる。
㋒より、( 192 + □ + 210 ) は 7 の倍数である。
210 は 7 の倍数なので、( 192 + □ ) が 7 の倍数となる □ を求める。
㋒より、□ は 65、66、67、68、69 のいずれかである。
192 + 67 = 259 = 7 × 37 より、□ = 67