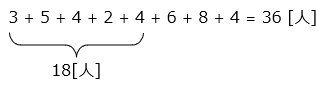算数【応用】平均

問１

ウォーキングが趣味しゅみの A 君のお父さんは、毎日歩いた歩数を記録しています。先週の平日（月曜日から金曜日）における歩数の平均は 12600 歩でした。日曜日は、家でのんびり過ごす時間が多かったため、土曜日の半分の歩数しか歩くことができず、月曜日から日曜日までの 1 週間の平均の歩数は 10500 歩でした。土曜日の歩数を求めなさい。

答え

7000 歩

解き方

1 週間に歩いた歩数の合計は 10500 × 7 = 73500 [歩]
平日に歩いた歩数の合計は 12600 × 5 = 63000 [歩]
よって、土曜日と日曜日に歩いた歩数の合計は、
73500 – 63000 = 10500 [歩]
土曜日の歩数を □ 歩とすると、日曜日の歩数は \(\dfrac{1}{2}\) × □ [歩] と表すことができ、次の式が成り立つ。
□ + \(\dfrac{1}{2}\) × □ = 10500
\(\dfrac{3}{2}\) × □ = 10500
□ = 10500 × \(\dfrac{2}{3}\) = 7000 [歩]

問２

A 組の人数は 30 人、B 組の人数は 20 人です。A 組と B 組で算数のテストをしたところ、A 組の平均点は B 組の平均点よりも 5 点高く、A 組と B 組を合わせた平均点は 69 点でした。B 組の平均点は何点でしたか。

答え

66 点

解き方

A 組と B 組を合わせた合計点は 69 × ( 30 + 20 ) = 3450 [点]
B 組の平均点を □ 点とすると、A 組の平均点は □ + 5 [点] と表すことができ、次の式が成り立つ。
30 × ( □ + 5 ) + 20 × □ = 3450
50 × □ = 3450 – 150 = 3300
□ = 66 [点]

【別解】面積図を利用する

　 部分と 　 部分の面積は互いに等しい。
横の長さの比は 3：2 より、縦の長さの比は 2：3 となる。
したがって、A 組と B 組を合わせた平均点と B 組の平均点の差は 3 点となる。
よって、B 組の平均点は 69 – 3 = 66 [点]

問３

A 組と B 組の 2 クラスで同じテストを 20 人ずつ受けました。A 組の方が平均点が高かったとき、次のア～ウから必ず正しいことをすべて選びなさい。

ア.　2 クラスの中で 1 番高い点を取った人は A 組にいる。

イ.　各クラスの点数が高いほうから 10 番目の人の点を比べると、A 組の人の方が高い。

ウ.　クラス全員の合計点は A 組の方が高い。

答え

ウ

解き方

ウ：クラスの合計点は、平均点 × 20 となる。よって、平均点の高い A 組の方が高くなる。

問４

あるテストで、A さん B さんの 2 人の平均点は 7 点、C さん D さん E さんの 3 人の平均点は 5 点、F さん G さん H さん I さんの 4 人の平均点は 4 点でした。A さんから I さんまでの 9 人の合計点を答えなさい。

答え

45 点

解き方

A さんから I さんの点数をそれぞれ a、b、c、d、e、f、g、h、i とすると、以下の式が成り立つ。
a + b = 2 × 7 = 14 ・・・ ①
c + d + e = 3 × 5 = 15 ・・・ ②
f + g + h + i = 4 × 4 = 16 ・・・ ③
① + ② + ③ より、
a + b + c + d + e + f + g + h + i = 14 + 15 + 16 = 45 [点]

問５

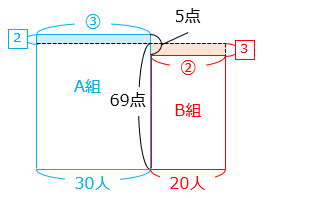
テストを 10 回受けます。9 回目までの平均点が 68 点でした。10 回目に何点以上取ると、10 回のテストの平均点が 70 点以上になりますか。

答え

88 点以上

解き方

10 回目に □ 点を取ったとき 10 回の平均が 70 点になるとすると、次の式が成り立つ。
□ = 70 × 10 – 68 × 9
□ = 700 – 612 = 88 [点]
よって、10 回の平均が 70 点以上になるのは10 回目に 88 点以上取ったとき。

【別解】面積図を利用する

　 部分と 　 部分の面積は互いに等しい。
横の長さの比は 9：1 より、縦の長さの比は 1：9 となる。
\(\boxed{1}\) = 70 – 68 = 2 [点] より、\(\boxed{9}\) = 9 × 2 = 18 [点]
よって、10 回の平均が 70 点以上になるのは10 回目に 70 + 18 = 88 [点] 以上取ったとき。

問６

算数と理科の平均点は 69.5 点で、国語、社会、英語の平均点が 57 点でした。このとき、5 教科すべての平均点は何点ですか。

答え

62 点

解き方

( 69.5 × 2 + 57 × 3 ) ÷ 5 = 62 [点]

問７

A さん、B さん、C さん、D さんの 4 人が算数のテストを受けました。4 人の平均点は 76 点で、A さんの点数は B さんより 8 点高く、D さんの点数は B さんより 16 点高く、C さんの点数は他の 3 人の平均点より 4 点低い点数でした。B さんの点数は何点でしたか。

答え

69 点

解き方

A さん、B さん、C さん、D さんの点数をそれぞれ a 点、b 点、c 点、d 点とすると、以下の式が成り立つ。
a + b + c + d = 76 × 4 = 304 ・・・ ①
a = b + 8 ・・・ ②
d = b + 16 ・・・ ③
c = ( a + b + d ) ÷ 3 – 4 ・・・ ④
④ を ② と ③ で置き換えると、
c = ( b + 8 + b + b + 16 ) ÷ 3 – 4
= ( 3 × b + 24 ) ÷ 3 – 4
= b + 8 – 4 = b + 4 ・・・ ④’
① を ②③④’ で置き換えると、
b + 8 + b + b + 4 + b + 16 = 304
4 × b + 28 = 304
4 × b = 304 – 28 = 276
b = 69 [点]

問８

5 個のおもり A、B、C、D、E があります。重さについて、A と B の平均は 48 g、B と C と D の平均は 65 g、C と D と E の平均は 53 g です。また、E の重さは A の重さより 42 g 重いです。

（１）5 個のおもりの重さの平均を求めなさい。

答え（１）

51 g

解き方（１）

おもり A、B、C、D、E の重さをそれぞれ a [g]、b [g]、c [g]、d [g]、e [g] とすると、以下の式が成り立つ。
a + b = 48 × 2 = 96 ・・・ ①
b + c + d = 65 × 3 = 195 ・・・ ②
c + d + e = 53 × 3 = 159 ・・・ ③
① + ③ より、
a + b + c + d + e = 96 + 159 = 255 ・・・ ④
5 個のおもりの重さの平均は、
( a + b + c + d + e ) ÷ 5 = 255 ÷ 5 = 51 [g]

（２）A と E の重さの平均を求めなさい。

答え（２）

30 g

解き方（２）

④ を ② で置き換えると、
a + 195 + e = 255
a + e = 255 – 195 = 60
A と E の重さの平均は、
( a + e ) ÷ 2 = 60 ÷ 2 = 30 [g]

（３）C と D の重さの平均を求めなさい。

答え（３）

54 g

解き方（３）

E の重さは A の重さより 42 g 重いことから、次の式が成り立つ。
e = a + 42 ・・・ ⑤
② – ① より、
c + d – a = 195 – 96 = 99 ・・・ ⑥
③ を ⑤ で置き換えると、
c + d + a + 42 = 159
c + d + a = 159 – 42 = 117 ・・・ ⑦
⑥ + ⑦ より、
2 × ( c + d ) = 99 + 117 = 216
c + d = 108
C と D の重さの平均は、
( c + d ) ÷ 2 = 108 ÷ 2 = 54 [g]

問９

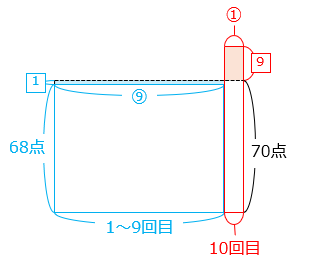
表はあるクラスの 10 点満点の漢字テストの結果です。中央値は何点ですか。

ヒント

中央値とは、データの数値を小さい（または大きい）順に並べたときのちょうど真ん中の値のこと。データの個数が偶数の場合は、中央の 2 つの値の平均値が中央値となる。

答え

7.5 点

解き方

クラスの人数を求める。

より、18 人目と 19 人目の点数の平均が中央値となる。
18 人目の点数は 7 点、19 人目の点数は 8 点より、
( 7 + 8 ) ÷ 2 = 7.5 [点]

問１０

A さんは同じ読書クラブのメンバー 19 人に対して「先週 1 週間に本を何冊読んだか」の調査を行ったところ、最も多い人で 17 冊の本を読んだ人がいることがわかりました。A さんは、調査結果を次のようなドットプロットにまとめましたが、1 人分の結果を見落としてしまい、図には 18 人分の結果しか反映されていません。

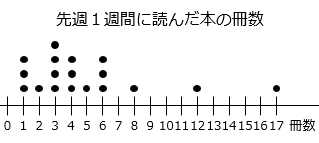
（１）19 人が読んだ本の冊数の中央値を求めなさい。

答え（１）

4 冊

解き方（１）

調査した人数は 19 人なので、10 人目の冊数が中央値となる。

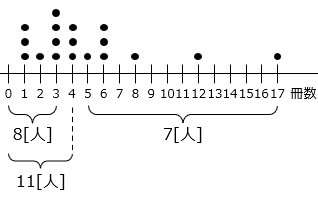
図より、見落としていた人が読んだ冊数が何冊であっても、中央値は 4 冊となる。

（２）19 人が読んだ本の冊数の平均値は整数であることがわかっています。このとき、A さんが結果を見落としてしまった 1 人について、その人が先週 1 週間に読んだ本の冊数を求めなさい。

答え（２）

6 冊

解き方（２）

18 人が読んだ本の総数を求めると、
1 × 3 + 2 + 3 × 4 + 4 × 3 + 5 + 6 × 3 + 8 + 12 + 17 = 89 [冊]
19 人が読んだ本の冊数の平均値は整数であることから、19 人が読んだ本の総数は19 の倍数になる。
89 ÷ 19 = 4 あまり 13

よって、 6 冊。

（３）19 人が読んだ本の冊数の平均値と中央値のどちらが大きいかは、上のどっとプロットを見れば平均値や中央値を計算せずに判断することができます。その判断の理由として最も適切なものをア～エから 1 つ選びなさい。

ア. 0 冊または 1 冊の本を読んだ人が少ないから。

イ. 1 冊、3 冊、4 冊のように、ドットプロットの「山」があるから。

ウ. 2 冊、5 冊のように、ドットプロットに「へこみ」があるから。

エ. 12 冊、17 冊のように、極端きょくたんに多くの本を読んだ人がいるから。

答え（３）

エ