算数【入試】比例と反比例
問1
A、B、C、D の 4 人である仕事をすると、仕上げるのに 28 時間かかります。この仕事を仕上げる時間について以下の ①、②、③ がわかっています。
① A が 1 人ですると、B、C、D が 3 人でするときの 4 倍の時間がかかる。
② A、B が 2 人ですると、C、D が 2 人でするときの 1.2 倍の時間がかかる。
③ C が 1 人ですると、D が 1 人でするときの 2 倍の時間がかかる。
(1)A が 1 人でこの仕事を仕上げるのに何時間かかりますか。
- 答え(1)
- 140 時間
- 解き方(1)
- 仕事の速さは、仕事にかかる時間に反比例する。
① より仕事の速さの比は、A:B + C + D = \(\dfrac{1}{4}\):1 = 1:4 とわかる。
A の仕事の速さを \(\boxed{1}\) とすると、4 人でするときの仕事の速さは \(\boxed{5}\) であるから、すべての仕事の量は \(\boxed{5}\) × 28 = \(\boxed{140}\) となる。
よって A が 1 人でするのにかかる時間は、
\(\boxed{140}\) ÷ \(\boxed{1}\) = 140 [時間]
(2)B が 1 人でこの仕事を仕上げるのに何時間かかりますか。
- 答え(2)
- 110 時間
- 解き方(2)
- ② より仕事の速さの比は、A + B:C + D = \(\dfrac{1}{1.2}\):1 = 5:6 とわかる。
A の仕事の速さを \(\boxed{1}\) とすると、
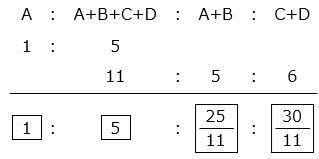
B の仕事の速さは \(\boxed{\dfrac{25}{11}}\) – \(\boxed{1}\) = \(\boxed{\dfrac{14}{11}}\) と表すことができる。
よって、B が 1 人でするのにかかる時間は、
\(\boxed{140}\) ÷ \(\boxed{\dfrac{14}{11}}\) = 110 [時間]
(3)C は 1 人でこの仕事を始めましたが、途中から D が加わり、C が始めてから 66 時間で仕上げました。C、D が 2 人で仕事をしたのは何時間ですか。
- 答え(3)
- 44 時間
- 解き方(3)
- ③ より仕事の速さの比は、C:D = \(\dfrac{1}{2}\):1 = 1:2 とわかる。
(2)より、A の仕事の速さを \(\boxed{1}\) とすると、C + D = \(\boxed{\dfrac{30}{11}}\) と表すことができる。
よって、C の仕事の速さは、
\(\boxed{\dfrac{30}{11}}\) × \(\dfrac{1}{3}\) = \(\boxed{\dfrac{10}{11}}\)
C、D が 2 人で仕事をしたのは、
( \(\boxed{140}\) – \(\boxed{\dfrac{10}{11}}\) × 66 ) ÷ ( \(\boxed{\dfrac{30}{11}}\) – \(\boxed{\dfrac{10}{11}}\) ) = 44 [時間]・・・つるかめ算を利用
問2
ある仕事を終えるのに機械 A は 5 日間、機械 B は 3 日間かかります。
(1)機械 A と機械 B に同時にこの仕事をさせたとき、仕事を終えるのに何日と何時間かかりますか。
- 答え(1)
- 1 日と 21 時間
- 解き方(1)
- 仕事の速さは仕事にかかる時間に反比例する。
よって、機械 A と B の仕事の速さは、A:B = \(\dfrac{1}{5}\):\(\dfrac{1}{3}\) = 3:5 となる。
A の仕事の速さを \(\boxed{3}\) とすると、この仕事の量は \(\boxed{3}\) × 5 = \(\boxed{15}\) となる。よって、
\(\boxed{15}\) ÷ ( \(\boxed{3}\) + \(\boxed{5}\) ) = 1\(\dfrac{7}{8}\) [日] ⇒ 1 日と 21 時間
(2)機械 A と機械 C に同時にこの仕事をさせたときと、機械 B と機械 C に同時にこの仕事をさせたときにかかった時間の比は 25:21 です。機械 C だけにこの仕事をさせたとき、仕事を終えるのに何日かかりますか。
- 答え(2)
- 2 日
- 解き方(2)
- 仕事の速さは、A + C:B + C = 21:25 となる。
A の仕事の速さを \(\boxed{3}\) とすると、
( \(\boxed{3}\) + C ):( \(\boxed{5}\) + C ) = 21:25
25 × ( \(\boxed{3}\) + C ) = 21 × ( \(\boxed{5}\) + C )
C = \(\boxed{\dfrac{15}{2}}\)
全体の仕事の量は \(\boxed{15}\) なので、
\(\boxed{15}\) ÷ \(\boxed{\dfrac{15}{2}}\) = 2 [日]
(3)機械 A が 7 台、機械 B が 1 台、機械 C が 4 台あります。この 12 台で、この仕事の 14 倍をさせるとき、仕事を始めた日時が 3 月 1 日 13 時であれば、終わるのは何月何日何時でしょうか。ただし、機械はすべて、毎日 22 時から翌日 8 時まで停止し、それ以外の時間はすべて仕事をさせることとします。
- 答え(3)
- 3 月 7 日 19 時
- 解き方(3)
- A の仕事の速さを \(\boxed{3}\) とすると、停止せずに仕事をさせたときにかかる時間は、
( \(\boxed{15}\) × 14 ) ÷ ( \(\boxed{3}\) × 7 + \(\boxed{5}\) + \(\boxed{\dfrac{15}{2}}\) × 4 ) = \(\dfrac{15}{4}\) [日] = 90 [時間]
機械は 1 日に 10 時間停止し、1 回目は 9 時間後、以降 14 時間ごとに 1 回停止する。
( 90 – 9 ) ÷ 14 = 5 余り 11 より、機械は全 6 回停止する。
よって、6 日後と 11 時間動いた日時の 3 月 7 日 19 時となる。
問3
イベントの食事係になりました。予算の金額で、ジュースならばちょうど 84 本、パンならば 30 個、お菓子は 70 個買うことができます。ジュース 1 本とパン 1 個とお菓子 1 個を 1 人分とすると、予算内で参加者全員分を買うことができ、お金は 420 円余ります。人数がもう 1 人多いと、予算では足りません。
(1)イベントの参加者は何人ですか。
- 答え(1)
- 16 人
- 解き方(1)
- ジュース 84 本、パン 30 個、お菓子 70 個の金額が等しいことより、それぞれ 1 個あたりの金額の比は個数に反比例する。
よってそれぞれ1個の金額の比は、
ジュース:パン:お菓子 = \(\dfrac{1}{84}\):\(\dfrac{1}{30}\):\(\dfrac{1}{70}\) = 5:14:6
よって、予算は \(\boxed{5}\) × 84 = \(\boxed{420}\)、1 人分の金額は 5 + 14 + 6 の \(\boxed{25}\) となる。
\(\boxed{420}\) ÷ \(\boxed{25}\) = 16 余り \(\boxed{20}\)
よって、参加者は 16 人。
(2)予算はいくらですか。
- 答え(2)
- 8820 円
- 解き方(2)
- \(\boxed{20}\) が 420 円に当たるので、
\(\dfrac{\boxed{420}}{\boxed{20}}\) × 420 = 8820 [円]
問4
歯車 A と歯車 B がかみ合って回転しています。歯車 A は歯数が 36 個で、5 分間で 150 回転します。歯車 B は 7 分間で 420 回転するとき、歯車 B の歯数は何個ですか。
- 答え
- 18 個
- 解き方
- 歯車がかみ合うとき、同じ時間あたりに歯が送り出される数、すなわち歯数と回転数の積は一定である。
よって、歯数の比は回転数に反比例する。
A と B の歯数の比は、A:B = \(\dfrac{1}{150\ ÷\ 5}\):\(\dfrac{1}{420\ ÷\ 7}\) = 2:1
B の歯数は、36 × \(\dfrac{1}{2}\) = 18 [個]
問5
家から公園まで、姉は 15 分で、妹は 20 分で歩きます。2 人はこの速さで 25 km のハイキングコースを歩きました。姉は 30 分歩くごとに 10 分の休憩をとったので、3 時間 35 分かかりました。妹も 30 分歩くごとに 10 分の休憩をとりました。妹は何時間何分かかりましたか。
- 答え
- 4 時間 50 分
- 解き方
- 姉と妹が同じ距離を歩くのにかかる時間の比は、姉:妹 = 15:20 = 3:4 である。
姉が休憩をとった回数は、( 3 × 60 + 35 ) ÷ ( 30 + 10 ) = 5 余り 15 より 5 回。
休憩を除いて姉がかかった時間は、215 – 5 × 10 = 165 [分] となる。
同じ速さで歩く場合、かかった時間は距離に比例するので、距離が変わってもかかる時間の比は同じである。
休憩を除いて妹が歩くのにかかった時間は、
165 × \(\dfrac{4}{3}\) = 220 [分]
妹が休憩した回数は、220 ÷ 30 = 7 余り 10 より 7 回。よって、休憩を入れた時間は、
220 + 7 × 10 = 290 [分] ⇒ 4 時間 50 分

