算数【入試】方陣算

問１

図(A)のような、一辺が5個の正方形の形に置いた碁石を、図(B)のように、たての列の個数が図(A)と同じようになるように並べかえます。すると図(B)は、たての列が3列と余り1個となります。このように一辺が5個以上の正方形を並べかえたときの余りの個数のことを「端数」と呼ぶことにします。図のように一辺が5個の場合は「端数が1」となります。

(1) 一辺が7個の正方形を並べかえたときの端数を求めなさい。

(2) 端数が5となるときの碁石の総数を求めなさい。

答え(1)

3

答え(2)

32個

解き方(1)

一辺が7個のときの碁石の個数は、(7 – 1) × 4 = 24(個)
24 ÷ 7 = 3あまり3
より、端数は3

解き方(2)

碁石の総数は一辺の個数の4倍より4個少ないので、端数に4を加えた数が一辺の碁石の個数になる。端数が5の場合、一辺の個数は5 + 4 = 9(個)となる。よって総数は、(9 – 1) × 4 = 32(個)

問２

図1のように、10000個の碁石を正方形の形に並べます。次に、図2のように一番外側の1周部分の碁石を取りのぞきます。同じようにして、順に外側の碁石を取りのぞく操作を、碁石が4個残るまで続けます。

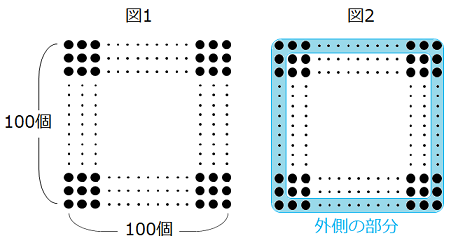
(1) 20回目の操作の後、残った碁石は何個ですか。

(2) 何回目かの操作の後、それまでに取りのぞいた碁石を合計した個数が、残った碁石の個数より初めて多くなりました。何回目の操作ですか。

(3) ある1回の操作で取りのぞいた碁石を全部使って、正方形の形に並べられる場合があります。初めにできるのは10回目ですが、次に正方形の形に並べられるのは何回目ですか。

答え(1)

3600個

答え(2)

15回目

答え(3)

26回目

解き方(1)

残った正方形の一辺に並ぶ碁石は、100 – 20 × 2 = 60(個)である。よって、60 × 60 = 3600(個)。
※1回の操作で、一辺に並ぶ碁石の個数は2個減る。

解き方(2)

残る個数が5000個以下になる最大の個数を考える。70 × 70 = 4900、72 × 72 = 5184より、一辺に並ぶ碁石の個数が70個の場合があてはまる。よって、(100 – 70) ÷ 2 = 15(回目)。

解き方(3)

取りのぞく碁石の個数が平方数になる場合を考える。10回目の操作で取りのぞく外側の一辺に並んだ碁石の数は、9回取り除いた状態の碁石なので、(100 – 9 × 2) = 82(個)。このとき取りのぞく碁石の個数は(82 – 1) × 4 = 81 × 4 = 9 × 9 × 4(個)。取りのぞく碁石の個数は、一辺が奇数個 × 4になるため、次に平方数になるのは、7 × 7 × 4 = 49 × 4となる。すなわち一辺に並んだ碁石の個数が50個の場合で、(100 – 50) ÷ 2 = 25回取りのぞいた状態である。したがって、25 + 1 の26回目になる。

問３

一辺に7個のおはじきを並べて正方形をつくりました。次に図1から図2さらに図3のように外側におはじきの列を増やしていきます。図2、図3はそれぞれおはじきを2列、3列並べたものです。

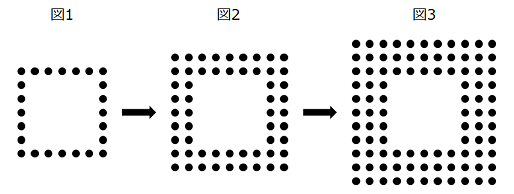
(1) 一番外側の列に並ぶおはじきの数が1000個になるのは、おはじきを何列並べたときですか。

(2) 並べたおはじきの総数が10000個に一番近くなるのは、おはじきを何列並べたときですか。

答え(1)

123列

答え(2)

48列

解き方(1)

おはじきの数が1000個になるとき、一辺に並ぶおはじきの数は1000 ÷ 4 + 1 = 251(個)。内側のおはじきがない部分には、一辺5個のおはじきが並ぶ。よって、(251 – 5) ÷ 2 = 123(列)

解き方(2)

内側のおはじきがない部分には、5 × 5 = 25(個)のおはじきを並べることができる。この25個を加えた10025個に近くなればよい。10025 – 99 × 99 = 224、101 × 101 – 10025 = 176より、一番外側の一辺におはじきが101個ならぶときがあてはまる。よって、(101 – 5) ÷ 2 = 48(列)

問４

図のように、何個かの碁石を、縦・横が同じ数になるように並べると、13個余りました。さらに、縦・横1列ずつ増やすには、あと38個足りません。碁石は全部で何個ありますか。

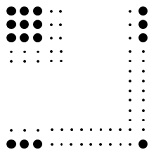
答え

638個

解き方

縦・横1列ずつ増やすために必要な碁石の数は、13 + 38 = 51(個)とわかる。よって、列を増やす前の一辺には、(51 – 1) ÷ 2 = 25(個)の碁石が並んでいることがわかる。碁石の総数は、25 × 25 + 13 = 638(個)

問５

図のように、碁石を並べて、正三角形、正四角形(正方形)、正五角形、・・・と全ての辺の長さが等しい図形を作ります。このとき、図形の辺の本数と1つの辺に並べる碁石の個数が等しくなるようにします。例えば、正三角形は辺が3本あるので、1つの辺に3つの碁石を並べて正三角形を作ります。いま、碁石が150個あります。できるだけたくさん使って、1つの図形を作るとき、できる図形の1つの辺には何個の碁石が並びますか

答え

12個

解き方

一辺に並ぶ碁石の数は正N角形ではN個となり、正N角形を作るために必要な碁石の数は、(N – 1) × N(個)となる。よって、150を超えないできるだけ大きなNの値を求める。
N = 12、(12 – 1) × 12 = 132
N = 13、(13 – 1) × 13 = 156
よって、12個