算数【基本】樹形図

問１

A、B、C、D、E の 5 人が並びます。A と B がこの順で並び、さらに B が最後にならないようにするとき、並び方は何通りありますか。

答え

18 通り

解き方

A – B の順は決まっているので、\(\boxed{A-B}\) を 1 組として考える。
求める \(\boxed{A-B}\)、C、D、E の並び方を樹形図で示した。


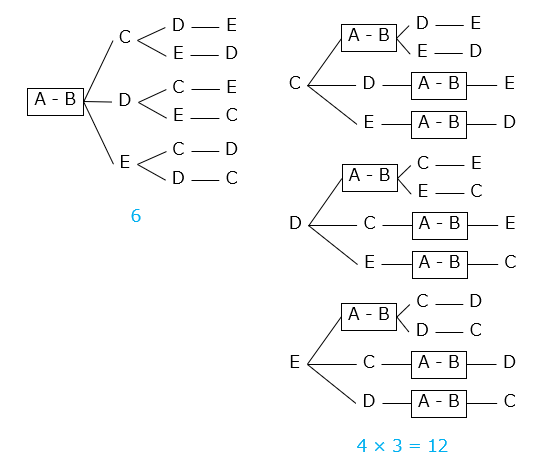
【別解】順列の式で解く
\(\boxed{A-B}\) を 1 組とし、すべての \(\boxed{A-B}\)、C、D、E の並び方は、
4 × 3 × 2 × 1 = 24 [通り]
そのうち、\(\boxed{A-B}\) が最後になる並び方は、
3 × 2 × 1 × 1 = 6 [通り]
よって求める並び方は、24 – 6 = 18 [通り]

問２

1000 円札 1 枚、500 円硬貨 2 枚、100 円硬貨 3 枚で支払える金額は何通りありますか。

答え

19 通り

解き方

組み合わせを樹形図で示した。


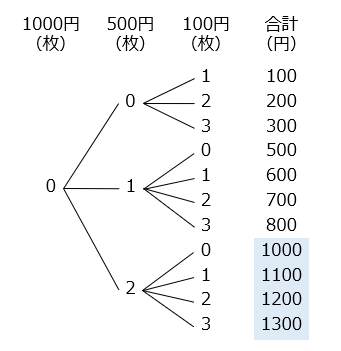
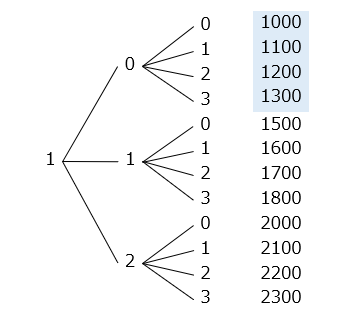
19 通り

問３

\(\boxed{1}\)、\(\boxed{2}\)、\(\boxed{3}\)、\(\boxed{4}\) の番号の書かれた箱が 1 個ずつと、①、②、③、④ の番号の書かれた玉が 1 個ずつあります。4 個の箱に玉をそれぞれ 1 個ずつ入れるとき、箱の番号と中に入れた玉の番号がすべて異なる場合は何通りありますか。

答え

9 通り

解き方

条件に合う組み合わせを樹形図で示した。

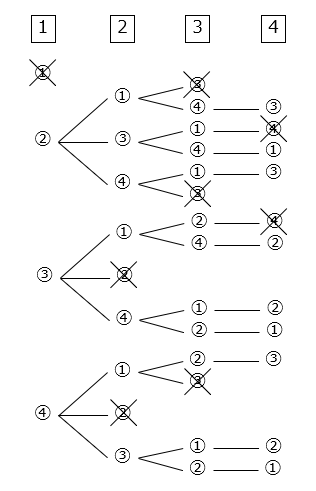
9通り

問４

100 円玉、50 円玉、10 円玉がたくさんあります。合計が300 円になる組み合わせは全部で何通りありますか。

答え

16 通り

解き方

300円になる組み合わせを樹形図で示した。

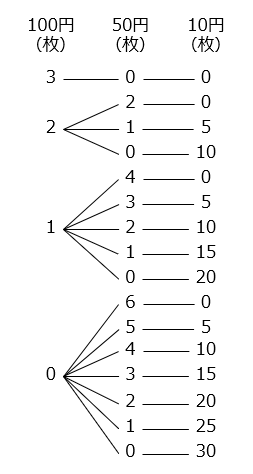
16 通り

問５

\(\boxed{1}\)、\(\boxed{2}\)、\(\boxed{3}\)、\(\boxed{4}\) のカードから 3 枚を並べて 3 けたの整数をつくります。230 より大きい数は何個ありますか。

答え

16 通り

解き方

230 より大きくなる組み合わせを樹形図で示した。

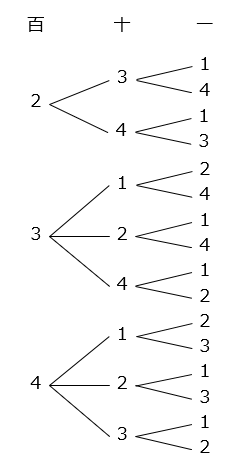
16 通り

問６

\(\boxed{0}\)、\(\boxed{1}\)、\(\boxed{2}\)、\(\boxed{4}\)、\(\boxed{5}\) の 5 枚のカードから 3 枚を選び、3 けたの数をつくります。このとき、421 は小さい方から数えて何番目ですか。

答え

32 番目

解き方

百の位が 1 または 2 となる 3 けたの数は、2 × 4 × 3 = 24 [個] ある。
百の位が 4、十の位が 0 または 1 の 3 けたの数は、1 × 2 × 3 = 6 [個] ある。
百の位が 4、十の位が 2 の 3 けたの数は、

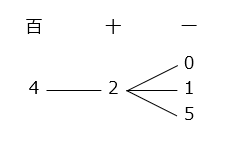
421 は 2 番目
よって、421 は小さい方から 24 + 6 + 2 = 32 [番目]

※樹形図ですべてを書き出しても良いが、数が多いと、書き出すのに時間がかかったり、数え間違いも生じやすい。計算式も利用しよう！

問７

下記 ２ つのルールに従って、コインが 0 枚になるまで操作をくり返します。

● コインの枚数が奇数の場合は、1 枚引かれる。

● コインの枚数が偶数の場合は、半分の枚数になる。

（１）最初のコインの枚数が 6 枚のとき、6 → 3 → 2 → 1 → 0 と 4 回の操作でコインが 0 枚になります。コインが 10 枚のとき、何回の操作でコインが 0 枚になりますか。

答え（１）

5 回

解き方（１）

10 → 5 → 4 → 2 → 1 → 0 より5回

（２）5 回の操作でコインが 0 枚になるのは、最初のコインが何枚のときですか。すべて答えなさい。

答え（２）

7 枚、9 枚、10 枚、12 枚、16 枚

解き方（２）

逆算すると、

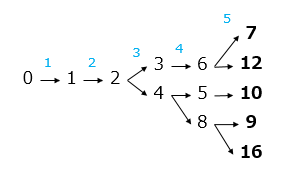
7, 9, 10, 12, 16 [枚]

（３）表は、操作の回数と最初のコインの枚数の関係をまとめたものです。㋐、㋑ に当てはまる数をそれぞれ答えなさい。

答え（３）

㋐：8　㋑：21

解き方（３）

逆算すると、奇数の前は偶数の 1 通り、偶数の前は奇数と偶数の 2 通りが考えられる。

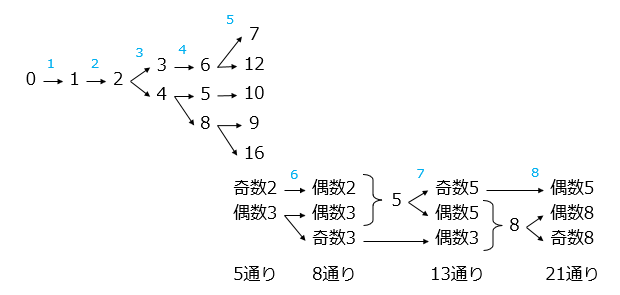
㋐：8 通り、㋑：21 通り