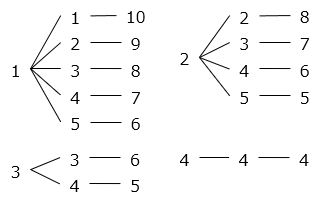算数【入試】樹形図

問１

4 を 0 以外の 3 つの整数の和で表す方法は、「1 + 1 + 2」の 1 種類あります。ただし、「1 + 2 + 1」、「2 + 1 + 1」は「1 + 1 + 2」と同じ種類と考えます。また、8 の場合は「1 + 1 + 6」、「1 + 2 + 5」、「1 + 3 + 4」、「2 + 2 + 4」、「2 + 3 + 3」の 5 種類あります。12 の場合は何種類の表し方がありますか。

答え

12

解き方

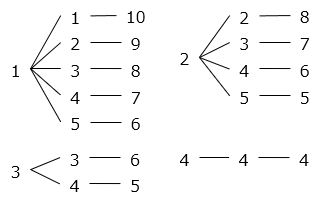
問２

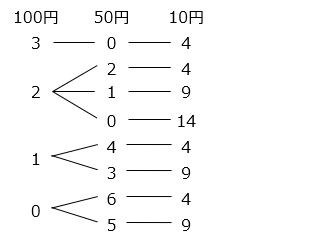
10 円、50 円、100 円、500 円の 4 種類の硬貨を、どの硬貨も 1 枚以上使って、合計金額を 1000 円にする方法を考えます。4 種類の硬貨の合計枚数が 20 枚以下になる場合は何通りありますか。

答え

8 通り

解き方

どの硬貨も 1 枚は使うので、硬貨 20 – 4 = 16 [枚] 以下で、1000 – ( 10 + 50 + 100 + 500 ) = 340 [円] になる場合を考える。500 円は 1 枚で 340 円をこえているので、100 円、50 円、10 円で 340 円にする場合を考える。

問３

5匹の犬 A、B、C、D、Eがいて、それぞれのための小屋 A、B、C、D、E があります。あるとき、5 つの小屋に犬が 1 匹ずつ入っていましたが、自分の小屋にいたのは 1 匹だけでした。5 匹の犬の、このような小屋への入り方は全部で何通りですか。

答え

45 通り

解き方

犬 A が自分の小屋に入っていたとき、ほかの 4 匹の小屋への入り方は、

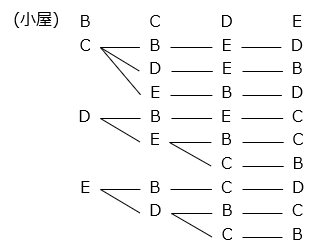
9 通りある。A 以外の 4 匹の犬がそれぞれ自分の小屋に入っていた場合も 9 通りずつあるので、9 × 5 = 45 [通り]

問４

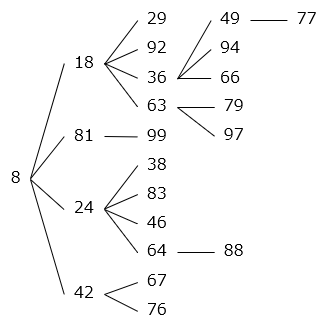
下の例のように、ある整数のすべての位の数をかけ合わせて、その答えが1けたの数になるまで繰り返します。

例) 48 → 4 × 8 = 32 → 3 × 2 = 6

最後の答えが8になる2けたの整数は何個ありますか。

答え

22個

解き方

問５

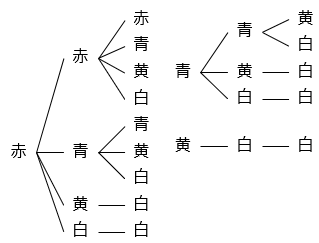
赤玉が 3 個、青玉が 2 個、黄玉が 1 個、白玉が 2 個あります。この中から同時に 3 個取り出すとき、取り出し方は何通りありますか。ただし、同じ色の玉を取ってもよいこととします。

答え

14 通り

解き方