算数【応用】角度
問1
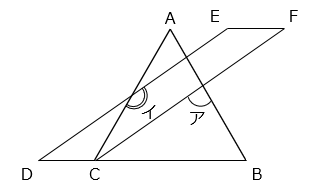
図で、三角形 ABC は正三角形で、四角形 CDEF は平行四辺形です。アの角度が 87 度であるとき、イの角度を求めなさい。
- 答え
- 153°
- 解き方
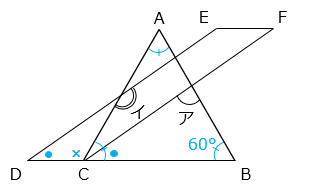
内角と外角の関係を利用する。
角イ = 角 ACD + 角 CDE と表すことができる。
角 ACD = 180 – 60 = 120 [°]
角 CDE = 角 BCF = 180 – ( 87 + 60 ) = 33 [°]
よって、角イ = 120 + 33 = 153 [°]
【別解】
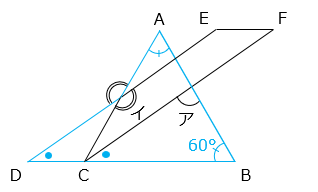
角イ = 角 CAB + 角 ABC + 角 CDE と表すことができる。
角 CAB = 角 ABC = 60°
角 CDE = 角 BCF = 180 – ( 87 + 60 ) = 33 [°]
よって、角イ = 60 + 60 + 33 = 153 [°]
問2
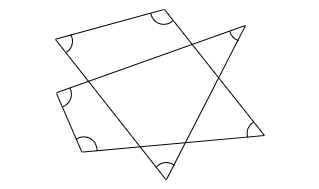
印をつけた角の角度の和は何度ですか。
- 答え
- 540°
- 解き方

図のように印のついた角に①~⑦の番号をつけ、印のない角には記号をつけると、以下の式が成り立つ。
① + ② + ⑤ + ⑦ + △ = 360 ・・・(ア)
③ + ④ + ⑤ + ⑦ + ○ = 360 ・・・(イ)
⑤ + ○ = ⑥ + ▲ ・・・(ウ)
⑦ + △ = ⑥ + ◎ ・・・(エ)
(ウ)+(エ)より、
⑤ + ⑦ + ○ + △ = 2 × ⑥ + ▲ + ◎・・・(オ)
▲ + ◎ = 180 – ⑥ より、
⑤ + ⑦ + ○ + △ = 2 × ⑥ + 180 – ⑥
⑤ + ⑦ + ○ + △ = ⑥ + 180 ・・・(オ)’
(ア)+(イ)より、
① + ② + ③ + ④ + ⑤ + ⑦ + ( ⑤ + ⑦ + ○ + △ ) = 720 ・・・(カ)
(カ)を(オ)で置き換えると、
① + ② + ③ + ④ + ⑤ + ⑦ + ⑥ + 180 = 720
① + ② + ③ + ④ + ⑤ + ⑥ + ⑦ = 720 – 180 = 540 [°]
問3
直線 l と m は平行で、三角形 ABC は正三角形です。このとき、角アの大きさを求めなさい。
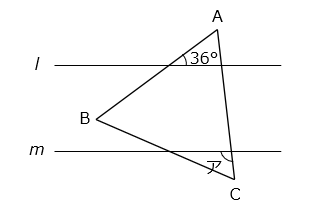
- 答え
- 96°
- 解き方
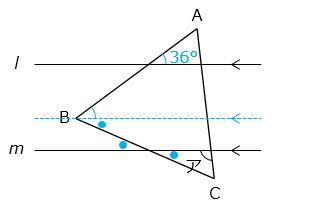
● の大きさは、60 – 36 = 24 [°]
よって、ア = 180 – ( 60 + 24 ) = 96 [°]
問4
四角形 ABCD は平行四辺形です。このとき、角アの大きさを求めなさい。ただし、同じ記号は同じ大きさを表します。
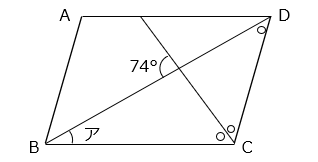
- 答え
- 21°
- 解き方
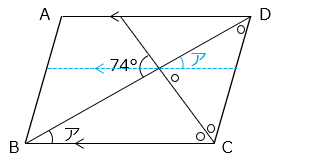
○ の大きさは、( 180 – 74 ) ÷ 2 = 53 [°]
ア = 74 – ○ = 74 – 53 = 21 [°]
問5
図のように、正方形の紙を AE を折り目として折り返したところ、点 B は点 F に移りました。このとき、角アの大きさを求めなさい。
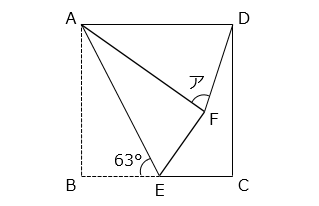
- 答え
- 72°
- 解き方
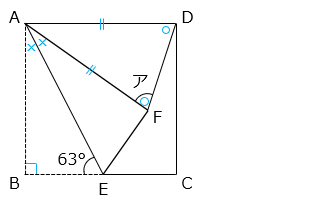
角 BAE(×)の大きさは、90 – 63 = 27 [°]
よって、角 DAF = 90 – 27 × 2 = 36 [°]
△ADF は AD = AF の二等辺三角形より、
ア = ( 180 – 36 ) ÷ 2 = 72 [°]
問6
図は、平行四辺形と直角三角形からできています。角アの大きさは何度ですか。
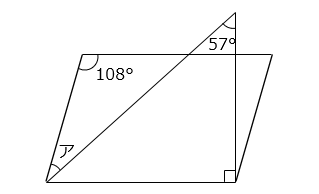
- 答え
- 39 度
- 解き方
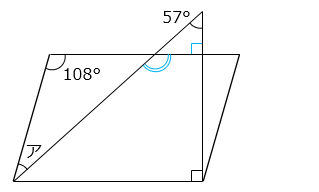
内角と外角の関係より、次の式が成り立つ。
ア + 108 = 57 + 90 = 147
ア = 147 – 108 = 39 [°]
問7
図の角アの大きさは何度ですか。
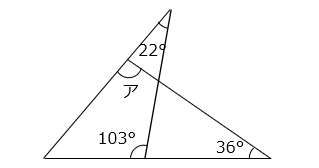
- 答え
- 89 度
- 解き方
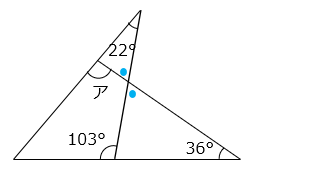
内角と外角の関係より、以下の式が成り立つ。
● = 103 – 36 = 67
ア = 22 + ● = 22 + 67 = 89 [°]
問8
図の角アの大きさは何度ですか。ただし、同じ印の角は同じ大きさです。
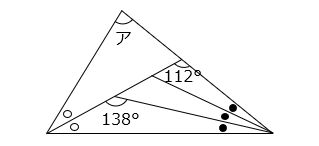
- 答え
- 83 度
- 解き方
- 内角と外角の関係より、以下の式が成り立つ。
ア + ○ = 112 ・・・①
112 + 2 × ● = 138 ・・・②
○ + ● = 180 – 138 = 42 ・・・③
② より、
2 × ● = 138 – 112 = 26
● = 13
③ より、
○ = 42 – ● = 42 – 13 = 29
① より、
ア = 112 – ○ = 112 – 29 = 83 [°]
問9
図のように、正五角形 ABCDE と正三角形 FCD があります。角アの大きさを答えなさい。
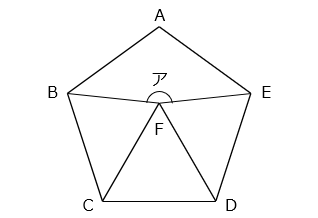
- 答え
- 168 度
- 解き方
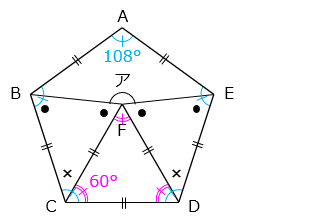
正五角形の内角の和は 180 × ( 5 – 2 ) = 540 [°] より、1 つの内角の大きさは 540 ÷ 5 = 108 [°]
正三角形の 1 つの内角の大きさは 60°
したがって、× = 108 – 60 = 48 [°] となる。
2 × ● = 180 – 48 = 132 [°]
よって、
ア = 360 – ( 60 + 132 ) = 168 [°]
問10
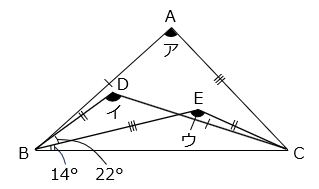
下の図形において、AB = CD、BD = CE、BE = AC で、角ア、角イ、角ウの大きさの和が 360° のとき、角ウの大きさを答えなさい。
- 答え
- 142 度
- 解き方
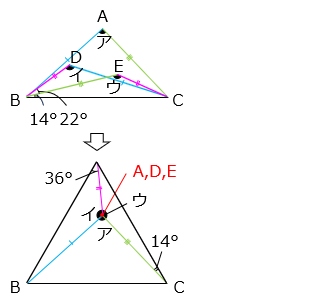
△ABC、△DBC、△EBC の各頂点 A、D、E を合わせると、1 辺の長さが BC の正三角形ができる。
正三角形の 1 つの内角の大きさは 60°
したがって、
ウ = 180 – 14 – ( 60 – 36 )
= 180 – 14 – 24 = 142 [°]
問11
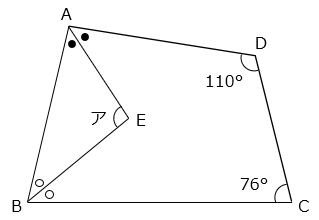
図のように四角形 ABCD があります。AE は角 A を二等分していて、BE は角 B を二等分しています。このとき、角アの大きさを答えなさい。
- 答え
- 93 度
- 解き方
- 四角形の内角の和は 360° より、
● + ○
= { 360 – ( 76 + 110 ) } ÷ 2
= ( 360 – 186 ) ÷ 2
= 174 ÷ 2 = 87 [°]
よって、
ア = 180 – 87 = 93 [°]





















