算数【入試】繰り返し（数列）

問１

次のような、ある決まりによって並べられた数の和を求めなさい。

5, 6, 7, 10, 11, 12, 15, 16, 17, . . . . . , 250, 251, 252

答え

19275

問２

次のように、数字がある決まりによって並んでいます。20番目の数字を答えなさい。

\(\frac{1}{33}\), \(\frac{3}{55}\), \(\frac{5}{77}\), \(\frac{7}{99}\), \(\frac{9}{1111}\), …..

答え

\(\frac{39}{4141}\)

問３

分母は１ずつ減少し、分子は３ずつ増加する以下に示した数列があります。１より大きな値になるのは何番目か答えなさい。

\(\frac{1}{2000}\), \(\frac{4}{1999}\), \(\frac{7}{1998}\), …..

答え

501

問４

ある決まりによって並べられた数字があります。

1, 3, 4, 6, 7, 9, 10, 12, …..

（１）123番目の数字を答えなさい。

（２）1527は何番目の数字か答えなさい。

答え（１）

184

答え（２）

1018

問５

どの桁も二つの数字1か0を使ってできる1以上の整数を小さいほうから順に並べた。このとき、43番目の整数を求めなさい。

1, 10, 11, 100, 101, 110, ・・・

答え

101011

ヒント

43を2進法で表す

問６

連続した奇数の和を求める方法を考えます。例えば1、3、5、7をその個数の〇で表し、図のようにカギ型に並べると、縦4つ、横4つの正方形状に並びます。空欄\(\boxed{(A)}\)、\(\boxed{(B)}\)にあてはまる数をそれぞれ求めなさい。

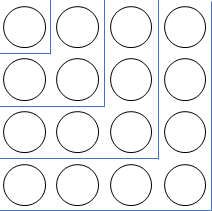
(1) 1 + 3 + 5 + ・・・ + 63 + 65 = \(\boxed{(A)}\times\boxed{(A)}\)

(2) 1 + 3 + 5 + ・・・ + \(\boxed{(B)}\) = 1600

答え(A)

33

答え(B)

79

ヒント(A)

65は何番目の奇数かを求める

ヒント(B)

1600 = 40 × 40、よって(B)は40番目の奇数

問７

規則的に数が並んでいます。

\(\dfrac{1}{1}\), \(\dfrac{1}{2}\), \(\dfrac{2}{1}\), \(\dfrac{1}{3}\), \(\dfrac{2}{2}\), \(\dfrac{3}{1}\), \(\dfrac{1}{4}\), \(\dfrac{2}{3}\), \(\dfrac{3}{2}\), \(\dfrac{4}{1}\), \(\dfrac{1}{5}\), \(\dfrac{2}{4}\), ・・・

値が\(\dfrac{1}{3}\)となる5番目の数は前から数えて何番目の数ですか。

答え

176番目

ヒント

上記の数の並びは、
\(\dfrac{1}{1}\) / \(\dfrac{1}{2}\), \(\dfrac{2}{1}\) / \(\dfrac{1}{3}\), \(\dfrac{2}{2}\), \(\dfrac{3}{1}\) / \(\dfrac{1}{4}\), \(\dfrac{2}{3}\), \(\dfrac{3}{2}\), \(\dfrac{4}{1}\) / \(\dfrac{1}{5}\), \(\dfrac{2}{4}\), ・・・
のようなグループに分けることができ、その中の数の個数は1, 2, 3, 4, ・・・と規則正しい数の並びになっている。値が\(\dfrac{1}{3}\)となる5番目の数は\(\dfrac{5}{15}\)であり、19番目のグループの5番目の数である。

問８

〇を図のように正三角形の形に並べたときの〇の総数、1、3、6、10、・・・を三角数といいます。

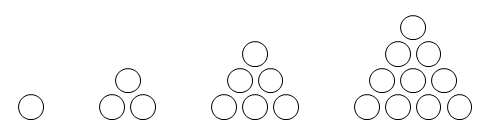
(1) 8番目の三角数はいくつですか。

(2) となり合う2つの三角数の和が1024のとき、その2つの三角数を求めなさい。

答え(1)

36

答え(2)

496, 528

ヒント(1)

n番目の三角数 = (1 + n) × n ÷ 2

ヒント(2)

となり合う2つの数なので 1024 ÷ 2 = 512 をはさんだ数である。(1 + n) × n ÷ 2 < 512 が当てはまる最大の整数が2つの数の小さい方である。