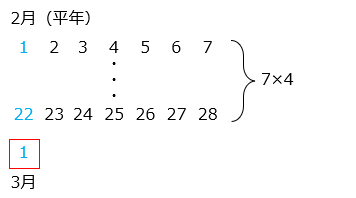算数【応用】日暦算
- ヒント
- ●大の月:31 日ある月 ⇒ 1 月、3 月、5 月、7 月、8 月、10 月、12 月
●小の月:31 日ない月「ニシムクサムライ」 ⇒ 2 月、4 月、6 月、9 月、11 月
●平年:2 月が 28 日で、1 年間が 365 日の年
●うるう年:2 月が 29 日で、1 年間が 366 日の年
西暦が 4 の倍数の年。ただし、100 の倍数の年は 400 の倍数の年のみうるう年となる。
【曜日の計算】
※1 か月後の曜日は、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ進み、平年の 2 月は同じ曜日となる
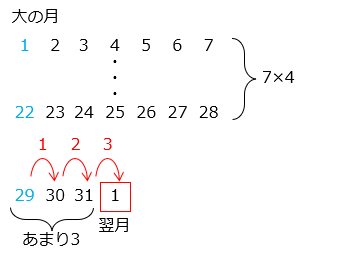
●大の月:31 ÷ 7 = 4 あまり 3
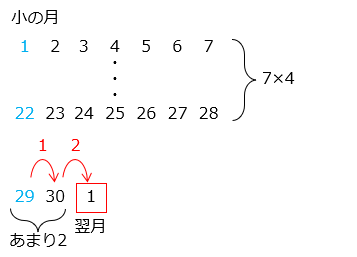
●小の月(2月を除く):30 ÷ 7 = 4 あまり 2
●2 月(平年):28 ÷ 7 = 4 あまり 0
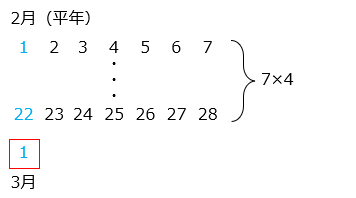
●2 月(うるう年):29 ÷ 7 = 4 あまり 1

※1 年後の曜日は、平年で 1 つ、うるう年では 2 つ進む
●平年:365 ÷ 7 = 52 あまり 1
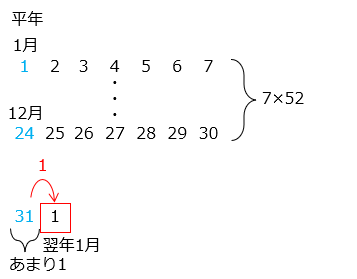
うるう年:366 ÷ 7 = 52 あまり 2
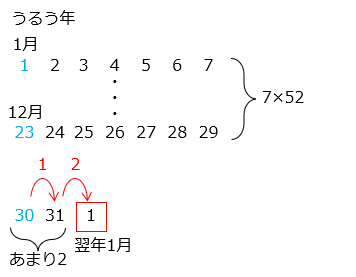
問1
(1)ある年の 4 月 8 日が月曜日のとき、同じ年の 7 月 2 日は何曜日ですか。
- 答え(1)
- 火曜日
- 解き方(1)
- 4 月 8 日から 7 月 2 日まで何日あるかを考える。
4 月は全部で 30 日より、8 日以降は 30 – 7 = 23 [日]。5 月は 31 日、6 月は 30 日あるので、7 月 2 日までは 23 + 31 + 30 + 2 = 86 [日]ある。
86 ÷ 7 = 12 あまり 2
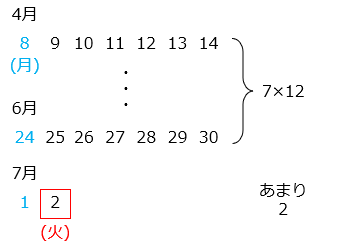
あまりの 2 は月曜から始まる 2 番目の曜日、火曜日となる。
【別解】「1 か月後の曜日は、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ進み、平年の 2 月は同じ曜日となる」を利用する
※間の月数が多いとき、覚えておくと便利
4 月と6 月は小の月なので 2 つずつ、5 月は大の月なので 3 つ、合わせて 7 つ曜日が進み、7 月 8 日は月曜日となる。よって、7 月 2 日は火曜日となる。
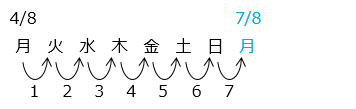
※ A 曜日からいくつ(何日)進む ⇒ A 曜日は含まず、「いくつ(何日)」ずれる。
(2)2023 年 6 月 1 日は木曜日です。2023 年 10 月の最初の木曜日は何日ですか。
- 答え(2)
- 5 日
- 解き方(2)
- まず、10 月 1 日の曜日を求める。
6 月と9 月は小の月なので 2 つずつ、7 月と8 月は大の月なので 3 つ、合わせて 10 曜日が進む。10 ÷ 7 = 1 あまり 3 より、10 月 1 日は木曜日から 3 つ進んだ日曜日となる。
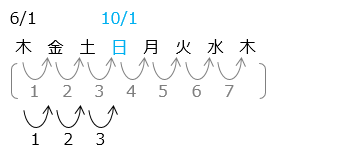
木曜日までは 4 日進むので、10 月の最初の木曜日は 5 日。
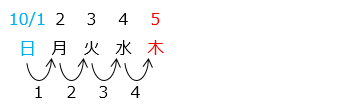
問2
2023 年 2 月 14 日は火曜日です。2025 年 2 月 14 日は何曜日ですか。
- 答え
- 金曜日
- 解き方
- 2023 年は平年より曜日は 1 進むので、2024 年 2 月 14 日は水曜日。
2024 年はうるう年より曜日は 2 進むので、2025 年 2 月 14 日は金曜日。
問3
平成 31 年は 4 月 30 日までで、翌 5 月 1 日から令和元年(令和 1 年)となりました。令和 5 年は西暦では 2023 年です。平成 19 年は西暦では何年ですか。
- 答え
- 2007 年
- 解き方
- 2024 年は令和 6 年より、令和元年(平成 31 年)は西暦では、2024 – ( 6 – 1 ) = 2019 [年]。
よって、平成 19 年は 2019 – ( 31 – 19 ) = 2007 [年]
問4
ある年の 4 月 1 日は日曜日です。この年の 1 日が日曜日である月は 4 月の他に何月ですか。ただし、この年はうるう年ではないとします。
- 答え
- 7 月
- 解き方
- 「1 か月後の曜日は、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ進み、平年の 2 月は同じ曜日となる」「1 か月前の曜日は前の月が、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ戻り、平年の 2 月は同じ曜日となる」を利用すると、
1 月 1 日は月曜日
2 月 1 日は木曜日
3 月 1 日は木曜日
5 月 1 日は火曜日
6 月 1 日は金曜日
7 月 1 日は日曜日
8 月 1 日は水曜日
9 月 1 日は土曜日
10 月 1 日は月曜日
11 月 1 日は木曜日
12 月 1 日は土曜日
問5
西暦 2024 年 2 月 1 日は木曜日です。次に 2 月 1 日が木曜日になるのは西暦何年ですか。ただし、西暦が 4 の倍数の年はうるう年です。
- 答え
- 2029 年
- 解き方
- 「1 年後の曜日は、平年で 1 つ、うるう年では 2 つ進む」を利用すると、
2025 年 2 月 1 日は土曜日
2026 年 2 月 1 日は日曜日
2027 年 2 月 1 日は月曜日
2028 年 2 月 1 日は火曜日
2029 年 2 月 1 日は木曜日
問6
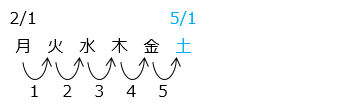
ある年の 2 月 1 日は月曜日です。この年の 5 月 1 日は何曜日ですか。ただし、この年はうるう年ではないものとします。
- 答え
- 土曜日
- 解き方
- 2 月 1 日から 5 月 1 日まで何日あるかを考える。
2 月は 28 日、3 月は 31 日、4 月は 30 日あるので、28 + 31 + 30 + 1 = 90 [日]ある。
90 ÷ 7 = 12 あまり 6
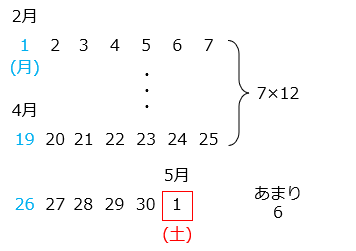
あまりの 6 は月曜から始まる 6 番目の曜日より、土曜日となる。
【別解】「1 か月後の曜日は、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ進み、平年の 2 月は同じ曜日となる」を利用する
2 月は 0、3 月は大の月なので 3、4 月は小の月なので 2、合わせて 5 つ曜日が進み、5 月 1 日は土曜日となる。
問7
2023 年 4 月 1 日を第 1 日とすると、2024 年 2 月 1 日は第何日目ですか。
- 答え
- 第 307 日目
- 解き方
- 2023 年 4 月 1 日から 2024 年 2 月 1 日まで何日あるかを考える。
2023 年 4 月、6 月、9 月、11 月は 30 日、5 月、7 月、8 月、10 月、12 月は 31 日、2024 年 1 月は 31 日あるので、30 × 4 + 31 × 6 + 1 = 307 [日]ある。
よって、第 307 日目。
問8
ある年の 5 月 3 日は金曜日でした。その翌年の 1 月 22 日は何曜日ですか。
- 答え
- 水曜日
- 解き方
- 5 月 3 日から翌年の 1 月 22 日まで何日あるかを考える。
5 月は全部で 31 日より、3 日以降は 31 – 2 = 29 [日]。6 月、9 月、11 月は 30 日、7 月、8 月、10 月、12 月は 31 日あるので、翌年の 1 月 22 日までは 29 + 30 × 3 + 31 × 4 + 22 = 265 [日]ある。
265 ÷ 7 = 37 あまり 6
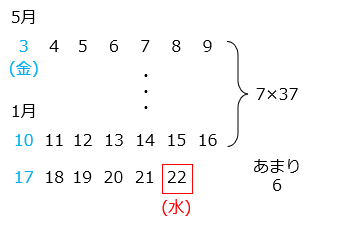
よって、水曜日となる。
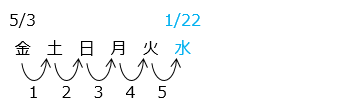
【別解】「1 か月後の曜日は、大の月は 3 つ、2 月を除く小の月は 2 つ、うるう年の 2 月は 1 つ進み、平年の 2 月は同じ曜日となる」を利用する
5 月、7 月、8 月、10 月、12 月は 3 ずつ、6 月、9 月、11 月は 2 ずつ、合わせて 3 × 5 + 2 × 3 = 21 [日] 進む。
21 ÷ 7 = 3 あまり 0 より、翌年の 1 月 3 日は金曜日。
1 月 22 日は、1 月 3 日 の 19 日後。
19 ÷ 7 = 2 あまり 5 より、1 月 22 日は水曜日。