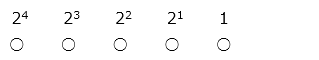算数【応用】N進法

問１

整数を次のように表すことにします。

1 は ○○○○●、2 は ○○○●○、3 は ○○○●●、4 は ○○●○○、5 は ○○●○●、6 は ○○●●○、・・・

（１）●●○●○ はいくつを表しますか。

答え（１）: 26

解き方（１）: ● が表す数字は図のように 2 進法の位取りになっている。

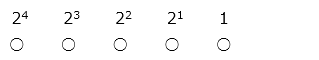
○○○○● ⇒ 1
○○○●○ ⇒ 2¹ = 2
○○○●● ⇒ 1 + 2¹ = 1 + 2 = 3
○○●○○ ⇒ 2² = 2 × 2 = 4
○○●○● ⇒ 1 + 2² = 1 + 4 = 5
○○●●○ ⇒ 2¹ + 2² = 2 + 4 = 6
したがって、
●●○●○ ⇒ 2¹ + 2³ + 2⁴
　　　　　　 = 2 + 2 × 2 × 2 + 2 × 2 × 2 × 2
　　　　　　 = 2 + 8 + 16 = 26

（２）28 を図で表すとき、ぬりつぶされる部分をすべて記号で答えなさい。

㋐㋑㋒㋓㋔

答え（２）: ア、イ、ウ

解き方（２）: 28 を 2 進法で表すと、図より、11100 となるので、1 がついている位をぬりつぶせばよい。
すなわち、ア、イ、ウ

問２

下のように「 0 」と「 1 」だけでできる 1 以上の整数を、小さい順に並べました。このとき、13 番目の数は何ですか。

1, 10, 11, 100, 101, 110, 111, 1000, ・・・

答え（１）: 1101

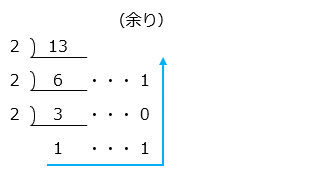
解き方（１）: 図より、13 を 2 進法で表すと 1101 となる。

問３

図のような「五個玉そろばん」があります。この「そろばん」において、一番右側の桁けたでは、玉を一個ずつ上にあげるにつれて、0 から 5 までの数を表すことができます。一番右側の桁の玉がすべて上にあがってしまったとき、次の数を表すには、一つ左の桁の玉を一個上にあげ、あがりきった右側の桁の玉はすべて下におろします。同様にして、≪ある桁≫の右側のすべての桁の玉がすべて上にあがってしまったとき、次の数を表すには、その≪ある桁≫の玉を一個あげ、あがりきった右側の桁の玉をすべて下におろします。そして、一番右側の桁の玉を一個ずつ上にあげてあとの数を表していきます。

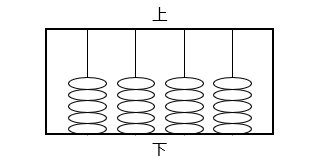
（１）次のア～ウの五個玉そろばんはそれぞれどんな数を表していますか。

ア

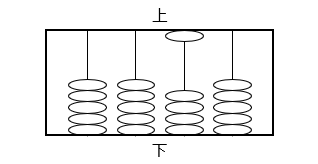
イ

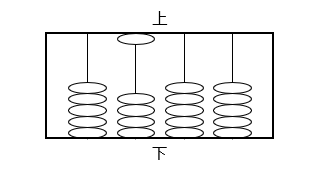
ウ

答え（１）: ア：6　イ：36　ウ：259

解き方（１）: 0 から 5 までの数を表す ⇒ 6 進法

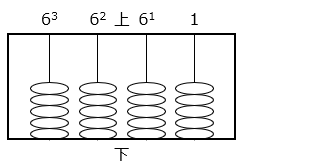
図のように、各桁の一番上の玉は右から 1 の位、6¹ の位、6² の位、6³ の位を表している。
ア：6¹ = 6
イ：6² = 6 × 6 = 36
ウ：1 + 6¹ + 6² + 6³
　　= 1 + 6 + 36 + 216 = 259

（２）1295 番目の数を表す五個玉そろばんをかきなさい。

答え（２）

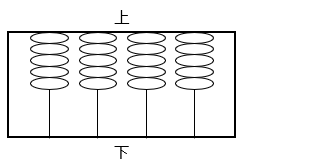
解き方（２）: 図より、1295 を 6 進法で表すと 5555 となる。