New当サイトが開発しました。立方体の切断面を実際の模型を使って学習できます。(メルカリにて販売中)

問1
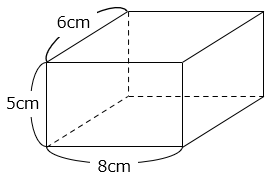
(1)直方体の体積を求めなさい。
- 答え(1)
- 240cm3
- 解き方(1)
- 5 × 8 × 6 = 240(cm3)
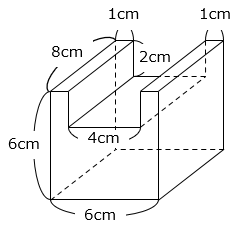
(2)図の立体の体積を求めなさい。
- 答え(2)
- 224cm3
- 解き方(2)
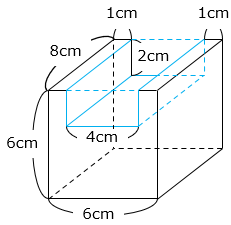
高さ6cm、横6cm、奥行き8cmの直方体から高さ2cm、横4cm、奥行き8cmの直方体を取りのぞいた立体図形の体積を求める。
6 × 6 × 8 – 2 × 4 × 8
= ( 36 – 8 ) × 8
= 28 × 8 = 224(cm3)
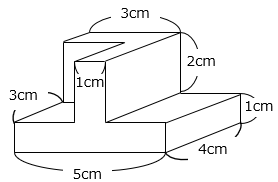
(3)図は直方体を組み合わせた立体です。この立体の体積を求めなさい。
- 答え(3)
- 32cm3
- 解き方(3)
- 【解き方①】3つの直方体の和と考える
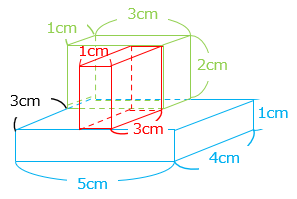
5 × 4 × 1 + 1 × 3 × 2 + 1 × 3 × 2
= 20 + 6 + 6= 32(cm3)
【解き方②】大きな直方体から2つの小さな直方体を除くと考える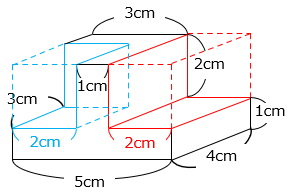
5 × 4 × 3 – 3 × 2 × 2 – 2 × 4 × 2
= 60 – 12 – 16
= 32(cm3)
(4)図は直方体から三角柱を切り取った立体です。この立体の体積を求めなさい。
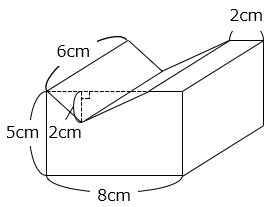
- 答え(4)
- 204cm3
- 解き方(4)
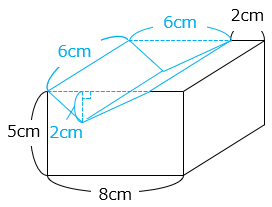
5 × 8 × 6 – 6 × 2 × \(\dfrac{1}{2}\) × 6
= 240 – 36
= 204(cm3)
(5)図は底面の半径が1cmの円柱と、底面の半径が10cmの円柱を組み合わせたものです。この立体の体積を求めなさい。ただし、円周率は3.14とします。
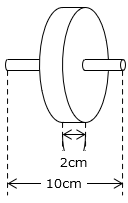
- 答え(5)
- 653.12cm3
- 解き方(5)
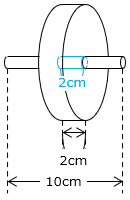
2つの円柱の体積の和から、重なった部分の体積を引く。
1 × 1 × 3.14 × 10 + 10 × 10 × 3.14 × 2 – 1 × 1 × 3.14 × 2
= ( 10 + 200 – 2 ) × 3.14
= 208 × 3.14
= 653.12(cm3)
(6)図の立体の体積を求めなさい。
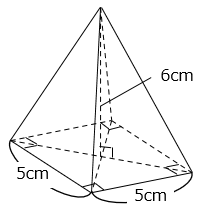
- 答え(6)
- 50cm3
- 解き方(6)
- 5 × 5 × 6 × \(\dfrac{1}{3}\) = 50(cm3)
(7)図の立体の体積を求めなさい。ただし、円周率は3.14とします。
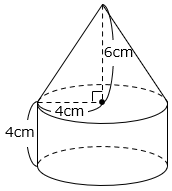
- 答え(7)
- 301.44cm3
- 解き方(7)
- 4 × 4 × 3.14 × 4 + 4 × 4 × 3.14 × 6 × \(\dfrac{1}{3}\)
= 64 × 3.14 + 32 × 3.14
= 96 × 3.14 = 301.44(cm3)
(8)1辺が1cmの立方体を5個使って図1のような立体をつくりました。この立体に上から薄い板を入れて切断し、2つの立体に分けます。図2は切断の様子を上から見た図です。このとき、体積が小さいほうの立体の体積を求めなさい。
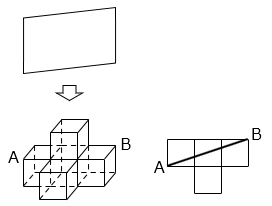
- 答え(8)
- 2cm3
- 解き方(8)
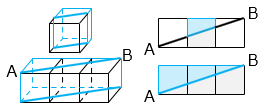
求める立体の体積は4個の立方体の半分の体積である。
1 × 1 × 1 × 4 ÷ 2 = 2(cm3)
(9)図は、ある立体を真正面と真上から見た図です。この立体の体積を求めなさい。
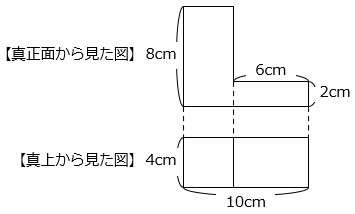
- 答え(9)
- 176cm3
- 解き方(9)
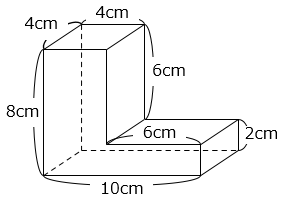
図の立体は、縦4cm、横10cm、高さ8cmの直方体から、縦4cm、横6cm、高さ6cmの直方体を取りのぞいた立体である。
4 × 10 × 8 – 4 × 6 × 6
= 320 – 144 = 176(cm3)
(10)図のように、直方体を組み合わせて階段状の立体をつくりました。表面積が386cm2であるとき、この立体の体積を求めなさい。
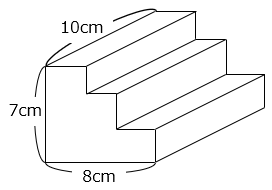
- 答え(10)
- 430cm3
- 解き方(10)
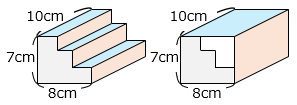
図の立体は、 部分を底面とする、高さ10cmの8角柱である。
部分の面積は、
{ 386 – ( 8 × 10 × 2 + 7 × 10 × 2 ) } ÷ 2
= ( 386 – 300 ) ÷ 2
= 86 ÷ 2 = 43(cm2)
よって、求める立体の体積は、
43 × 10 = 430(cm3)
(11)図は、ある立体を真正面と真上から見た図です。この立体の体積を求めなさい。ただし、円周率は3.14とする。
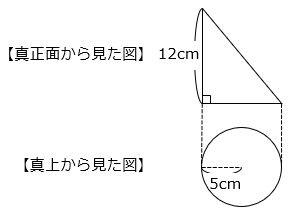
- 答え(11)
- 471cm3
- 解き方(11)
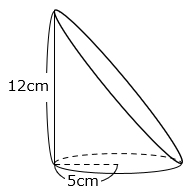
図の立体は、半径5cmの円を底面とする高さ12cmの円柱を、ななめに半分に切り取った立体である。
5 × 5 × 3.14 × 12 ÷ 2
= 150 × 3.14 = 471(cm3)
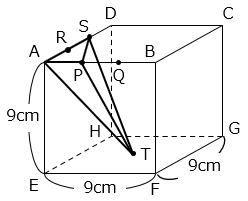
(12)図は、1辺9cmの立方体です。辺ABを3等分する点をP、Q、辺ADを3等分する点をR、S、面EFGH上の点をTとします。このとき、4点A、P、S、Tを結んでできる三角すいの体積を求めなさい。
- 答え(12)
- 27cm3
- 解き方(12)
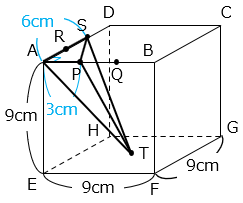
体積を求める立体は、直角三角形APSを底面とする高さ9cmの三角錐である。
3 × 6 × \(\dfrac{1}{2}\) × 9 × \(\dfrac{1}{3}\)
= 3 × 9 = 27(cm3)
(13)三角形ABCを底面とする 部分の三角柱の体積を求めなさい。
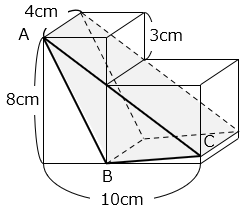
- 答え(13)
- 100cm3
- 解き方(13)
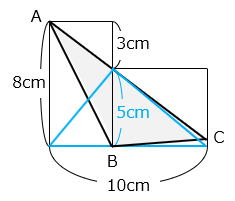
△ABCの面積は△の面積に等しい。
三角柱の面積は、
10 × 5 × \(\dfrac{1}{2}\) × 4 = 100(cm3)
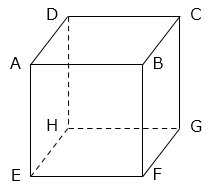
(14)図のような立方体ABCD-EFGHがあります。この立方体を、3つの頂点A、F、Hを通る平面で切ります。このときにできる小さいほうの立体の体積が150cm3のとき、立方体ABCD-EFGHの体積を求めなさい。
- 答え(14)
- 900cm3
- 解き方(14)
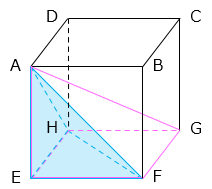
小さいほうの立体は、△EFHを底面とする三角すいA-EFHである。□EFGHを底面とする四角すいA-EFGHの体積はこの三角すいの体積の2倍であり、求める立方体の体積はこの四角すいの体積の3倍となる。
よって、求める体積は、
150 × 2 × 3 = 900(cm3)
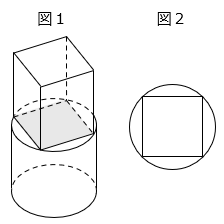
(15)図1は、円柱の上に底面が正方形の直方体をのせて作った立体です。どちらも高さは10cmです。図2は、この立体を真上から見たものです。 部分の面積が32cm2のとき、この立体の体積を求めなさい。ただし、円周率は3.14とします。
- 答え(15)
- 822.4cm3
- 解き方(15)
- 【解き方①】ひし形の面積の求め方(対角線 × 対角線 ÷ 2)を利用する
正方形はひし形にふくまれる。円柱の底面の円の直径を□cmとすると、
□ × □ ÷ 2 = 32
□ × □ = 64
□ = 8(cm)
よって、円柱の底面の円の半径は4cm
求める立体の体積は、4 × 4 × 3.14 × 10 + 32 × 10 = 822.4(cm3)
【解き方②】正方形を三角形に分割する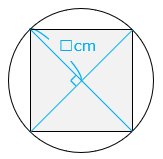
円柱の底面の円の半径を□cmとすると、
□ × □ ÷ 2 = 32 ÷ 4
□ × □ = 16
□ = 4(cm)
問2
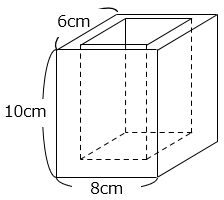
(1)図は縦6cm、横8cm、高さ10cmの直方体から、すべての面の厚みが1cmになるように直方体をくりぬいた立体です。この立体の表面積を求めなさい。
- 答え(1)
- 556cm2
- 解き方(1)
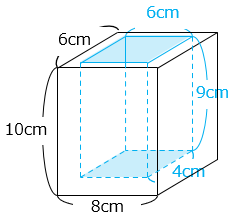
上部の面の欠けた部分と、くりぬかれた直方体の底面の面積は等しいので、表面積は大きい直方体の表面積と、くりぬかれた直方体の側面の面積の和になる。
10 × 8 × 2 + 10 × 6 × 2 + 8 × 6 × 2 + 9 × 6 × 2 + 9 × 4 × 2
= 160 + 120 + 96 + 108 + 72 = 556(cm2)
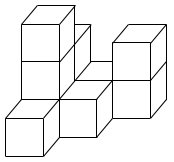
(2)図は1辺4cmの立方体を積み上げたものです。この立体の表面積を求めなさい。
- 答え(2)
- 608cm2
- 解き方(2)
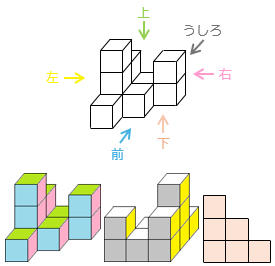
立方体の一面の面積は 4 × 4 = 16cm2
立体に表面に見えている立方体の面の数は、
6 + 6 + 7 + 6 + 7 + 6 = 38
この立体の表面積は、
16 × 38 = 608(cm2)
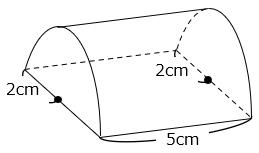
(3)図のように、底面が半径2cmの円柱を半分にした立体の表面積を求めなさい。ただし、円周率は3.14とします。
- 答え(3)
- 63.96cm2
- 解き方(3)
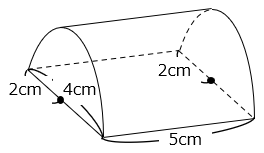
2 × 2 × 3.14 × \(\dfrac{1}{2}\) × 2 + 4 × 3.14 × \(\dfrac{1}{2}\) × 5 + 4 × 5
= 4 × 3.14 + 10 × 3.14 + 20
= 4 × 3.14 + 10 × 3.14 + 20
= 43.96 + 20 = 63.96(cm2)
(4)図のような、縦30cm、横10cm、高さ6cmの直方体があります。この直方体を㋐、㋑、㋒の面にそれぞれ平行な面で切り、いくつかの直方体に分けます。
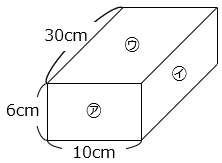
① ㋐の面に平行に1回切り2つの直方体に分けます。2つの直方体の表面積の合計を求めなさい。
- 答え(4)- ①
- 1200cm2
- 解き方(4)- ①
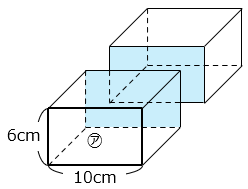
㋐の面に平行に1回切ると、切った後にできる直方体の表面積の合計は、切る前の直方体の表面積より㋐2面分の面積が増える。
切る前の直方体の表面積は、
( ㋐ + ㋑ + ㋒ ) × 2
= ( 6 × 10 + 6 × 30 + 10 × 30 ) × 2
= ( 60 + 180 + 300 ) × 2
= 540 × 2 = 1080(cm2)
㋐の面積は60cm2より、切った後に増えた面積は 60 × 2 = 120cm2
切った後にできる直方体の表面積の合計は、
1080 + 120 = 1200(cm2)
② ㋑の面と㋒の面に平行にそれぞれ何回か切って、いくつかの直方体に分けました。できた直方体の表面積の合計は3360cm2になりました。それぞれ何回切りましたか。
- 答え(4)- ②
- ㋑ 3回 ㋒ 2回
- 解き方(4)- ②
- ①より、切る前の直方体の面積は1080cm2なので、切った後に増えた面積は、
3360 – 1080 = 2280(cm2)
㋑の面に平行に1回切ったときに増える面積は、180 × 2 = 360(cm2)
㋒の面に平行に1回切ったときに増える面積は、300 × 2 = 600(cm2)
よって、㋒の面に平行に何回切っても増える面積の10の位は8にならない。
㋑の面に平行に切って、増える面積の10の位が8になるのは、3回と8回のときである。しかし、360 × 8 = 2880 > 2280より、3回である。
㋒の面に平行に何回か切ったときに増える面積は、
2280 – 360 × 3
= 2280 – 1080 = 1200(cm2)
よって、㋒の面に平行に切った回数は、1200 ÷ 600 = 2(回)
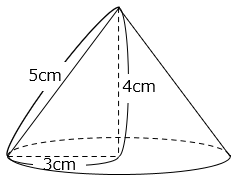
(5)図は、底面の半径が3cm、高さが4cm、母線の長さが5cmの円すいです。側面積を求めなさい。
- 答え(5)
- 47.1cm2
- 解き方(5)
- 5 × 5 × 3.14 × \(\dfrac{3\ ×\ 2\ ×\ 3.14}{5\ ×\ 2\ ×\ 3.14}\)
= 5 × 5 × 3.14 × \(\dfrac{3}{5}\)
= 5 × 3.14 × 3 = 47.1(cm2)
問3
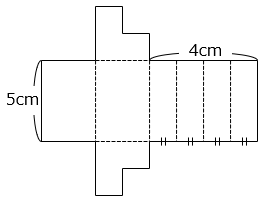
(1)図はある立体の展開図です。この立体の体積を求めなさい。
- 答え(1)
- 15cm3
- 解き方(1)
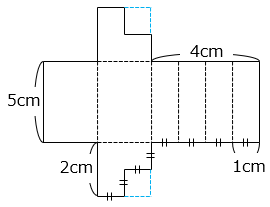
展開図の立体は、1辺2cmの正方形を底面に持つ高さ5cmの直方体から1辺1cmの正方形を底面に持つ高さ5cmの直方体を取りのぞいた立体である。
2 × 2 × 5 – 1 × 1 × 5
= 20 – 5 = 15(cm3)
(2)図の展開図を組み立ててできる立体の体積は218.5cm3、表面積は 130.8cm2 です。
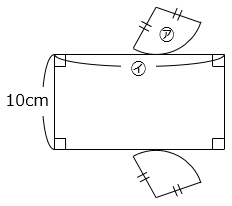
① おうぎ形㋐の面積を求めなさい。
- 答え(2)- ①
- 21.85cm2
- 解き方(2)- ①
- この展開図の立体はおうぎ形㋐を底面とする柱体。よっておうぎ形の面積は、
218.5 ÷ 10 = 21.85(cm2)
② ㋑の長さを求めなさい。
- 答え(2)- ②
- 8.71cm
- 解き方(2)- ②
- 側面の面積は、表面積からおうぎ形部分の面積を引いた面積なので、
130.8 – 2 × 21.85 = 87.1(cm2)
よって㋑の長さは、
87.1 ÷ 10 = 8.71(cm)
(3)図1は立方体の展開図です。
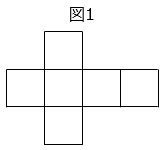
① 立方体の展開図はほかにもいろいろあります。次の図の(ア)~(オ)の中で、立方体の展開図としてふさわしくないものを1つ選びなさい。
- 答え(3)- ①
- エ
- 解き方(3)- ①
の面が重なる
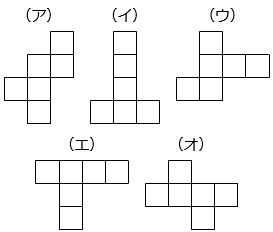
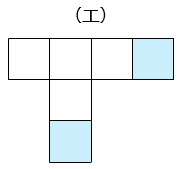
② 図2のように、立方体の箱にひもを六角形になるようにかけました。その後で、図3のように展開したとき、残りのひもの様子を展開図にかきなさい。
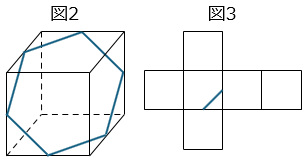
- 答え(3)- ②
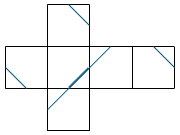
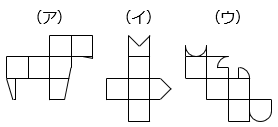
(4)次の3つの展開図のうち、組み立てたとき立方体になるのはどれですか。
- 答え(4)
- ウ
- 解き方(4)
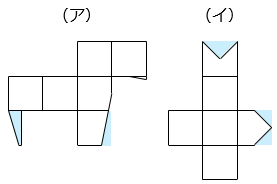
(ア) 部分が一致しない
(イ) 部分がすき間になる
(5)図1は同じ大きさの正三角形8枚で囲んだ立体です。この立体を図のように切って開いたとき、「2」を正しく書き入れなさい。
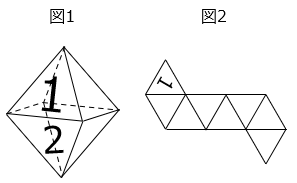
- 答え(5)
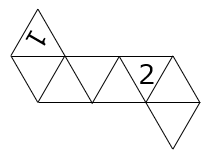
- 解き方(5)
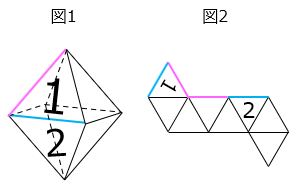
(6)図の展開図を組み立てると立体ができます。この立体の体積を求めなさい。
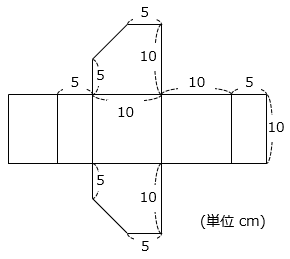
- 答え(6)
- 875cm3
- 解き方(6)
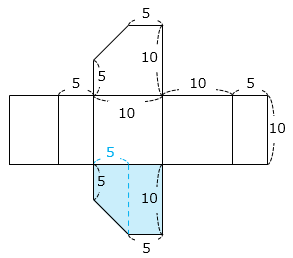
組み立ててできる立体は 部分を底面とする高さ10cmの五角柱である。
底面は長方形と台形を合わせた図形であり、その面積は、
10 × 5 + ( 5 + 10 ) × 5 ÷ 2
= 50 + 37.5 = 87.5(cm2)
五角柱の体積は、
87.5 × 10 = 875(cm3)
(7)図のような側面が合同な二等辺三角形の三角すいがあります。側面の三角形の等しい2辺の長さは6cm、その2辺がはさむ角は15°です。ひもを頂点Bから辺AC、AD、ABを通って頂点Cまで巻きつけます。ひもの長さが最も短くなるように巻きつけたとき、頂点Bから辺ADまでのひもの長さを求めなさい。
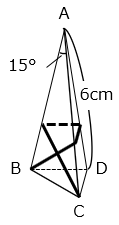
- 答え(7)
- 3cm
- 解き方(7)
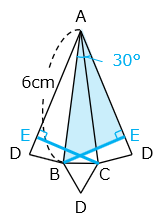
展開図を描いて考える。
ひもが辺ADを通る点をEとすると求める長さは点BからEまでのひもの長さと考えられる。このひもの長さが最も短くなるのは、点Bから辺ADまで垂直に伸ばしたときである。
このときできる△ABEは角Aが30°、角Bが60°の直角三角形となる。
よって、BE = 3(cm)
(8)図は、折り目となる線が書かれていない直方体の展開図です。この直方体の体積を求めなさい。
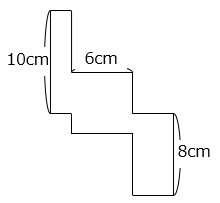
- 答え(8)
- 48cm3
- 解き方(8)
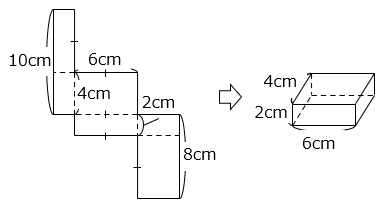
4 × 6 × 2 = 48(cm3)
問4
(1)図の の部分の図形を、直線Lを軸として、一回転してできる立体について答えなさい。ただし、円周率は3.14とします。
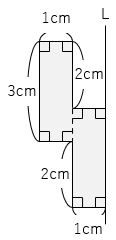
① この立体の体積を求めなさい。
- 答え(1)- ①
- 37.68cm3
- 解き方(1)- ①
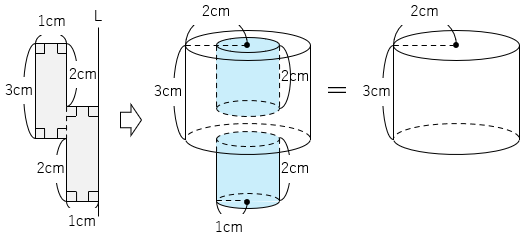
部分の体積は等しいので、この立体の体積は半径2cmの円が底面の高さ3cmの円柱の体積と同じになる。
2 × 2 × 3.14 × 3
= 12 × 3.14 = 37.68(cm3)
② この立体の表面積を求めなさい。
- 答え(1)- ②
- 87.92cm2
- 解き方(1)- ②
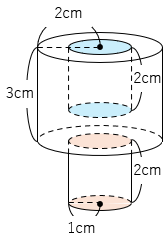
同じ色の部分の面積は互いに等しいので、この立体の表面積は半径の大きいほうの円柱の表面積と、半径が小さいほうの2つの円柱の側面の面積の和になる。
2 × 2 × 3.14 × 2 + 2 × 2 × 3.14 × 3 + 1 × 2 × 3.14 × 2 × 2
= 8 × 3.14 + 12 × 3.14 + 8 × 3.14
= 16 × 3.14 + 12 × 3.14
= 50.24 + 37.68 = 87.92(cm2)
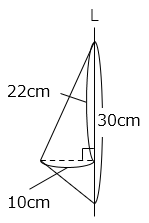
(2)直線Lに接している、図のような三角形があります。この三角形を直線Lを軸として、一回転してできる立体の体積を求めなさい。ただし、円周率は3.14とします。
- 答え(2)
- 3140cm3
- 解き方(2)
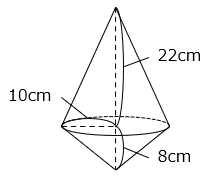
回転してできる立体の体積は、半径10cmの円を底面とした、高さ22cmの円すいと、高さ8cmの円すいの体積の和となる。
10 × 10 × 3.14 × 22 × \(\dfrac{1}{3}\) + 10 × 10 × 3.14 × 8 × \(\dfrac{1}{3}\)
= 2200 × 3.14 × \(\dfrac{1}{3}\) + 800 × 3.14 × \(\dfrac{1}{3}\)
= 3000 × 3.14 × \(\dfrac{1}{3}\)
= 1000 × 3.14 = 3140(cm3)
問5
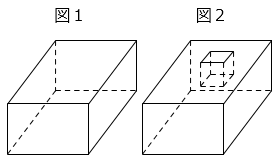
(1)図1の直方体から、1辺が3cmである立方体をくりぬいた立体が図2です。図2の立体の体積が193cm3のとき、直方体の3辺の長さを求めなさい。ただし、直方体の3辺の長さは整数で、どれも3cmより長いとします。
- 答え(1)
- 4cm、5cm、11cm
- 解き方(1)
- 直方体の体積は、
193 + 3 × 3 × 3
= 193 + 27 = 220(cm3)
220を3より大きい数で素因数分解すると、
220 = 4 × 5 × 11
よって3辺の長さは、4cm、5cm、11cm
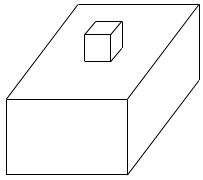
(2)図は、直方体の上に立方体をのせたものです。図の立体の表面積は、直方体の表面積より196cm2増えました。立方体の体積を求めなさい。
- 答え(2)
- 343cm3
- 解き方(2)
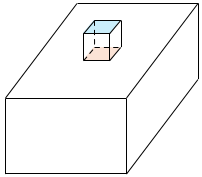
部分は直方体から減った面積、 部分は増えた面積であり、どちらも面積は等しい。
よって実際に増えたのは、立方体の側面4面分の面積に等しいことから、立方体一面の面積は、
196 ÷ 4 = 49(cm2)
立方体1辺の長さは、49 = 7 × 7 より、7cmである。
したがって、立方体の体積は、
49 × 7 = 343(cm3)
(3)図のように立方体を積み重ねて大きな立方体をつくりました。黒い円は、上と正面と横からそれぞれ向かいの面まで穴を通したものです。このとき、穴の開いていない立方体は何個ありますか。
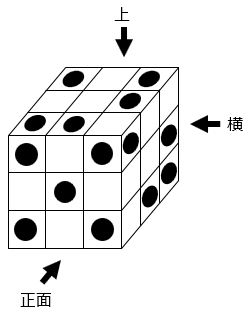
- 答え(3)
- 4個
- 解き方(3)
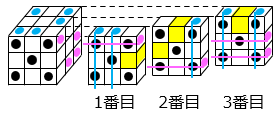
図のように立体を正面から1番目、2番目、3番目に分割して考える。
穴が開いていない立方体は、
1番目 1個
2番目 2個
3番目 1個
よって、全部で4個
(4)図のように、1辺が4cmの立方体8個を積み立てて立体をつくりました。この立体の表面に、1辺が2cmの正方形の色紙をすき間や重なりがないようにはっていきます。色紙は何枚必要ですか。ただし、底の部分にもはるものとします。
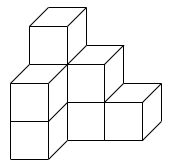
- 答え(4)
- 120枚
- 解き方(4)
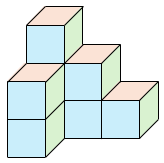
立体の面の数を求める。
正面から見た面( )の数と後ろから見た面の数、上から見た面( )の数と底の部分の面の数、右から見た面( )の数と左から見た面の数は、それぞれ等しい。
よって、立体の面の数は、( 6 + 4 + 5 ) × 2 = 30
1辺が4cmの面に1辺が2cmの色紙をはるには4枚必要なので、
30 × 4 = 120(枚)
New 当サイトが開発しました。立方体の切断面を実際の模型を使って学習できます。(メルカリにて販売中)

(5)図の立方体を、3点A、B、Cを通る平面で切ったとき、切り口の図形を(ア)~(オ)から選びなさい。
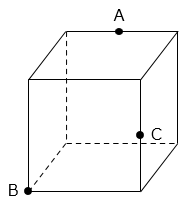
(ア)二等辺三角形
(イ)平行四辺形
(ウ)台形
(エ)五角形
(オ)六角形
- 答え(5)
- (エ)
- 解き方(5)
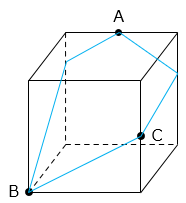
切り口の図形は五角形
