算数【応用】立体図形(体積・表面積・展開図)
問1
図のような直方体 ABCD-EFGH があります。直線 ℓ を回転の軸として、この直方体を 1 回転させます。ただし、円周率は 3.14 とします。
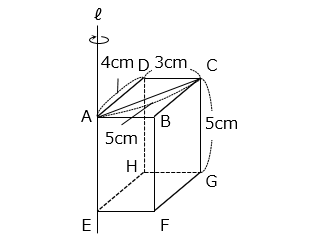
(1)面 AEFB が通過する部分の体積は何 cm3 ですか。
- 答え(1)
- 141.3 cm3
- 解き方(1)
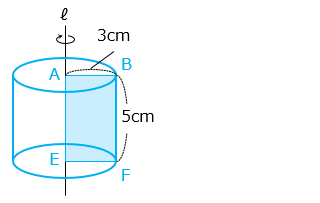
面 AEFB が通過する部分は、半径 3 cm の円を底面とする高さ 5 cm の円柱になる。よって、その体積は、
3 × 3 × 3.14 × 5 = 141.3 [cm3]
(2)面 BFGC が通過する部分の体積は何 cm3 ですか。
- 答え(2)
- 251.2 cm3
- 解き方(2)
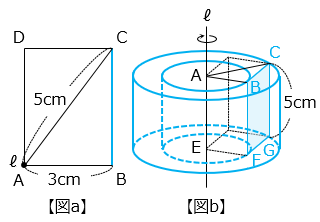
図 a は立体を真上から見た図である。
面 BFGC と直線 ℓ との距離は、点 A と辺 BC の距離と等しい。
図 a より、面 BFGC と直線 ℓ との距離は、最も短くて 3 cm、最も長くて 5 cm である。
よって面 BFGC が通過する部分は、半径 5 cm の円から半径 3 cm の円を除いた部分を底面とする、高さ 5 cm の立体となる ( 図 b )。よって、その体積は、
( 5 × 5 × 3.14 – 3 × 3 × 3.14 ) × 5
= ( 25 – 9 ) × 3.14 × 5
= 16 × 3.14 × 5 = 251.2 [cm3]
(3)面 DBFH が通過する部分の体積は \(\boxed{ア}\) × 3.14 cm3 です。\(\boxed{ア}\) に当てはまる数を答えなさい。
- 答え(3)
- 51.2
- 解き方(3)
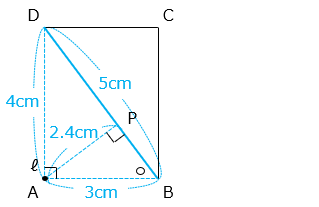
点 A から BD に垂直な直線と BD との交点を P とする。
図より、点 A からの距離が最も長いのは AD = 4 [cm]、最も短いのは AP である。
△ABD と△PBA は 2 つの角の大きさがそれぞれ等しい相似な三角形で、相似比は BD:BA = 5:3 である。よって、
PA = AD × \(\dfrac{3}{5}\)
= 4 × \(\dfrac{3}{5}\) = 2.4 [cm]面 DBFH が通過する部分は、半径 4 cm の円から半径 2.4 cm の円を除いた部分を底面とする、高さ 5 cm の立体となる。よって、その体積は、
( 4 × 4 × 3.14 – 2.4 × 2.4 × 3.14 ) × 5
= ( 16 – 5.76 ) × 3.14 × 5
= 10.24 × 3.14 × 5
= 51.2 × 3.14 [cm3]
問2
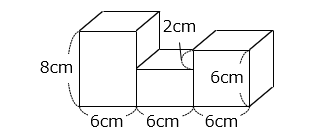
図のように、底面の縦の長さが同じで、横の長さが 6 cm の直方体を 3 つ組み合わせた立体の体積が 324 cm3 のとき、立体の表面積は何 cm2 ですか。
- 答え
- 384 cm2
- 解き方
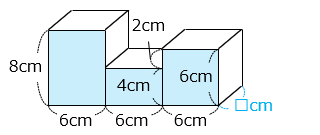
底面の縦の長さ ( □ cm ) は、
324 ÷ ( 8 × 6 + 4 × 6 + 6 × 6 )
= 324 ÷ { ( 8 + 4 + 6 ) × 6 }
= 324 ÷ ( 18 × 6 )
= 324 ÷ 108 = 3 [cm]
よって表面積は、
108 × 2 + 6 × 3 × 3 × 2 + 8 × 3 × 2 + 6 × 3 × 2 – 4 × 3 × 2
= 108 × 2 + ( 18 + 8 + 6 – 4 ) × 3 × 2
= 108 × 2 + 28 × 3 × 2
= ( 108 + 84 ) × 2
= 192 × 2 = 384 [cm2]
問3
図は立体の展開図です。ただし、点線は折り目ではありません。
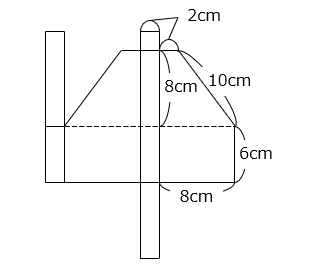
(1)立体の表面積は何 cm2 ですか。
- 答え(1)
- 256 cm2
- 解き方(1)
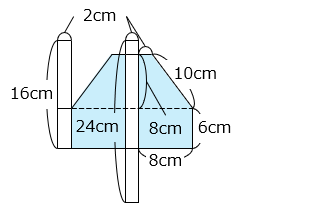
表面積は展開図の面積である。
図の 部分の面積は互いに等しい。 部分の面積は合わせて、
{ ( 2 + 8 ) × 8 ÷ 2 + 8 × 6 } × 2
= ( 10 × 8 ÷ 2 + 48 ) × 2
= ( 40 + 48 ) × 2
= 88 × 2 = 176 [cm2]
求める表面積は、
16 × 2 + 24 × 2 + 176
= 32 + 48 + 176 = 256 [cm2]
(2)立体の体積は何 cm3 ですか。
- 答え(2)
- 176 cm3
- 解き方(2)
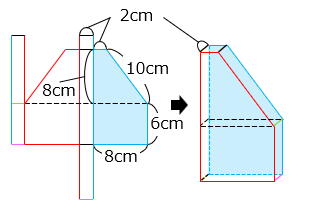
展開図より、 部分を底面とする高さ 2 cm の立体となる。
よってその体積は、
88 × 2 = 176 [cm3]
問4
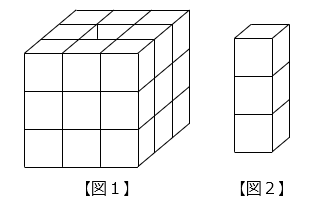
図 1 と図 2 は、1 辺が 1 cm の立方体を積み重ねた立体で、図 1 の中央の穴に図 2 を入れると、1 辺が 3 cm の立方体となります。このとき、図 1 の立体について以下の問いに答えなさい。
(1)立体の表面に色を塗りました。塗った面積は何 cm2 ですか。
- 答え(1)
- 64 cm2
- 解き方(1)
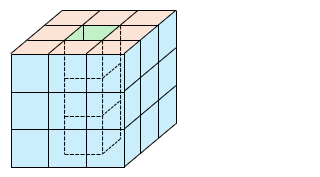
塗られた部分の面積は、立体の表面積である。
立体の上下の面 ( ) には 1 辺 1 cm の正方形が 8 個ずつある。
立体の外側の 4 つの側面 ( ) には 1 辺 1 cm の正方形が 9 個ずつある。
立体の内側の 4 つの側面 ( ) には 1 辺 1 cm の正方形が 3 個ずつある。
よって、その面積は、
8 × 2 + 9 × 4 + 3 × 4
= 16 + 36 + 12 = 64 [cm2]
(2)(1)で色を塗った立体について、積み重ねてある立方体を 1 つずつ調べて、色が塗られていない面がいくつあるか数えました。立体に使われている立方体をすべて調べたとき、色が塗られていない面は全部で何面ありますか。
- 答え(2)
- 80 面
- 解き方(2)
- 図 1 の立体に積み重ねられた立方体の個数は、
3 × 3 × 3 – 3 = 24 [個]
1 つの立方体の面は 6 面あるので、積み重ねられた立方体の面は全部で 6 × 24 = 144 [面] ある。
また、色が塗られた表面積は(1)より 64 cm2 なので、色が塗られた面は 64 面である。
したがって色が塗られていない面は、144 -64 = 80 [面]
問5
図は、立方体の展開図です。この展開図を組み立てたとき、A と重なる点を B ~ N から選びなさい。
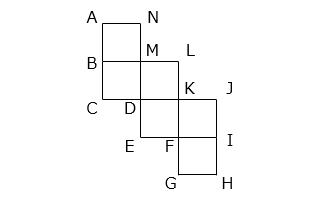
- 答え
- I
- 解き方
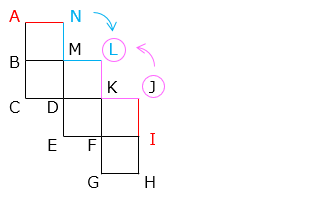
問6
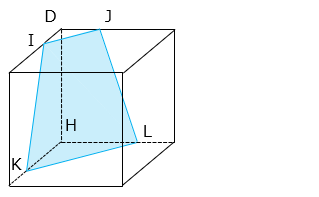
図 1 のような 1 辺の長さが 6 cm の立方体 ABCD-EFGH を、4 点 I、J、L、K を通る平面で切断した立体 DIJ-HKL があります。図 2 は面 ABCD、図 3 は面 EFGH を表し、 部分は立体 DIJ-HKL の面になります。
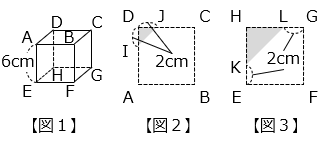
(1)三角形 DIJ と三角形 HKL の面積の比を、最も簡単な整数の比で書きなさい。
- 答え(1)
- 1:4
- 解き方(1)
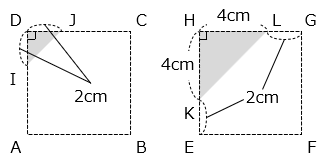
△DIJ と △HKL は互いに相似な直角二等辺三角形で、相似比は DI:HK = 2:4 = 1:2 となるので、その面積比は △DIJ:△HKL = 1:4 となる。
(2)面 IJLK はどのような形ですか。次のア~オから選びなさい。
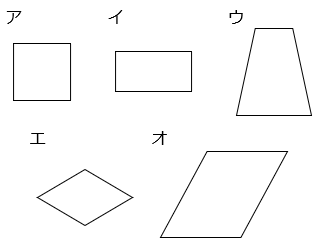
- 答え(2)
- ウ
- 解き方(2)
(3)立体 DIJ-HKL の体積は何 cm3 ですか。
- 答え(3)
- 28 cm3
- 解き方(3)
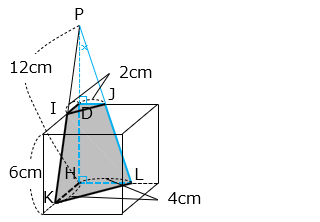
HD、KI、LJ を上へのばして交わる点を P とする。
△PHL と △PIJ は互いに相似な三角形で、相似比は HL:IJ = 4:2 = 2:1 である。
よって、PD = DH となり、PH = 12 [cm] である。
立体 DIJ-HKL の体積は、
4 × 4 × \(\dfrac{1}{2}\) × 12 × \(\dfrac{1}{3}\) – 2 × 2 × \(\dfrac{1}{2}\) × 6 × \(\dfrac{1}{3}\)
= 32 – 4 = 28 [cm3]
【別解】
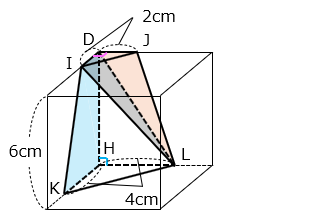
立体 DIJ-HKL を 3 点 D、I、L を通る面で切断すると、面 DIKH を底面とする四角すい L-DIKH と、面 DJL を底面とする三角すい L-DJL に分けられる。
四角すい L-DIKH の体積は、
( 2 + 4 ) × 6 × \(\dfrac{1}{2}\) × 4 × \(\dfrac{1}{3}\) = 24 [cm3]
三角すい L-DJL の体積は、
2 × 6 × \(\dfrac{1}{2}\) × 2 × \(\dfrac{1}{3}\) = 4 [cm3]
立体 DIJ-HKL の体積は、
24 + 4 = 28 [cm3]
問7
図のような 1 辺の長さが 8 cm の立方体があります。
ただし、(1)(2)(3)ともに、正方形の穴は面に対して垂直に、反対側の面まであけるものとします。
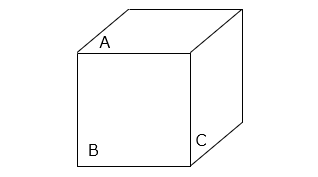
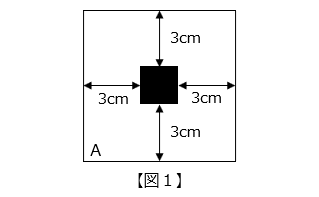
(1)【図 1】のように、立方体の A の面に、1 辺が 2 cm の正方形の穴を開けました。残った立体の体積は何 cm3 ですか。
- 答え(1)
- 480 cm3
- 解き方(1)
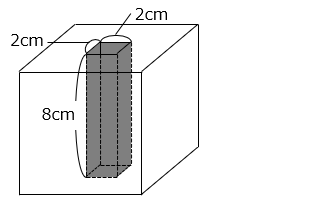
8 × 8 × 8 – 2 × 2 × 8
= ( 64 – 4 ) × 8
= 60 × 8 = 480 [cm3]
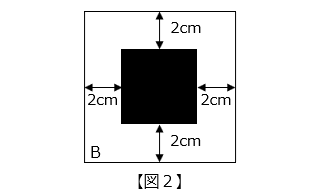
(2)(1)の作業のあとに、【図 2】のように、立方体の B の面に、1 辺が 4 cm の正方形の穴を開けました。残った立体の体積は何 cm3 ですか。
- 答え(2)
- 368 cm3
- 解き方(2)
(1)の作業のあとの立体から、B の面から開けられた1 辺が 4 cm の正方形の穴の体積を除くと、(1)で開けた穴と重なる部分を余計に除いたことになる。
よって、求める体積は、
480 – 4 × 4 × 8 + 2 × 2 × 4
= 480 – 128 + 16 = 368 [cm3]
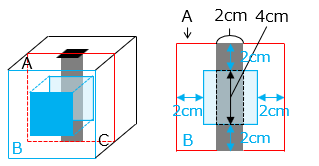
(3)さらに(2)の作業のあとに、【図 3】のように、立方体の C の面に、1 辺が 6 cm の正方形の穴を開けました。残った立体の体積は何 cm3 ですか。
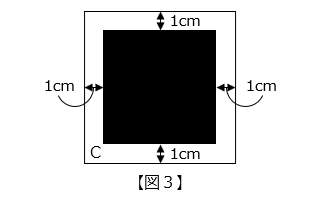
- 答え(3)
- 184 cm3
- 解き方(3)
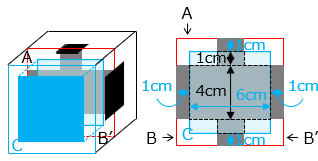
( 面 B’ は面 B の反対側の面 )
(2)の作業のあとの立体から、C の面から開けられた1 辺が 6 cm の正方形の穴の体積を除くと、(1)で開けた穴と(2)で開けた穴と重なる部分を余計に除いたことになる。
よって、求める体積は、
368 – 6 × 6 × 8 + 2 × 2 × 1 × 2 + 4 × 4 × 6
= 368 – 288 + 8 + 96 = 184 [cm3]
問8
図のような台形 ABCD を、辺 CD のまわりに 1 回転してできる立体の体積を求めなさい。ただし、円周率は 3.14 とします。
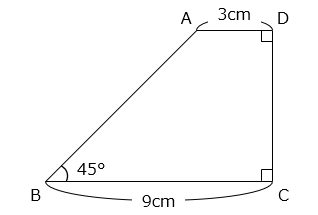
- 答え
- 734.76 cm3
- 解き方
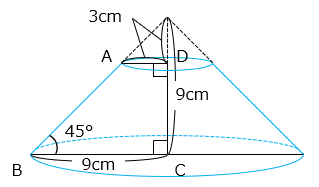
求める立体の体積は、半径 9 cm、高さ 9 cm の円すいの体積から、半径 3 cm、高さ 3 cm にの円すいの体積を除いたものである。
9 × 9 × 3.14 × 9 × \(\dfrac{1}{3}\) – 3 × 3 × 3.14 × 3 × \(\dfrac{1}{3}\)
= 243 × 3.14 – 9 × 3.14
= ( 243 – 9 ) × 3.14
= 234 × 3.14 = 734.76 [cm3]
問9
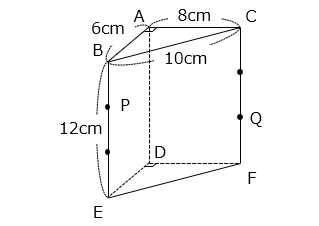
図のように、底面が直角三角形の三角柱があります。点 P、Q はそれぞれ辺 BE、辺 CF を 3 等分する点です。この三角柱を 3 つの点 A、P、Q を通る平面で切断しました。このとき、頂点 D をふくむ立体の体積は何 cm3 ですか。
- 答え
- 192 cm3
- 解き方
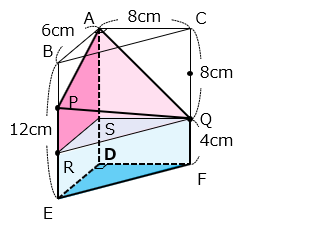
頂点 D をふくむ立体を点 Q、R を通り、面 DEF と平行な面で切断する。切断面と辺 AD の交点を S とすると、頂点 D をふくむ立体は、面 DEF を底面とする三角柱 EDF- SRQ と面 APRS を底面とする四角柱 APRS-Q に分けることができる。
よって求める立体の体積は、
8 × 6 × \(\dfrac{1}{2}\) × 4 + ( 4 + 8 ) × 6 × \(\dfrac{1}{2}\) × 8 × \(\dfrac{1}{3}\)
= 96 + 96 = 192 [cm3]
問10
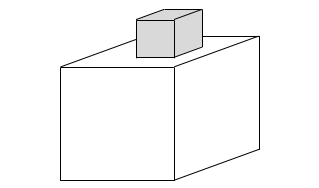
ある立方体の上に別の立方体をのせて、図のような新しい立体 X を作りました。立体 X の表面積は、もとの立方体の表面積より 256 cm2 増えています。このとき、のせた立方体の体積は何 cm3 ですか。
- 答え
- 512 cm3
- 解き方
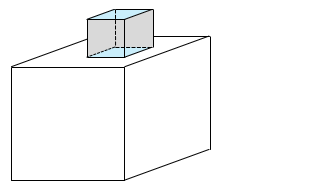
2 つの立方体が重なった部分の面積は、のせた立方体の上面の面積と等しいことから、増えた表面積はのせた立方体の 4 つの側面の面積と同じである。
のせた立方体の 1 辺の長さを □ cm とすると、次の式が成り立つ。
□ × □ × 4 = 256
□ × □ = 64
□ = 8 [cm]
よって、のせた立方体の体積は、
64 × 8 = 512 [cm3]
































