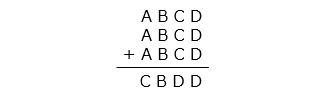算数【応用】四則計算(文章題)
問1
重さ 120 g の容器に、1 個 25 g の飴を 25 個入れました。全体の重さは何 g になりましたか。
- 答え
- 745 g
- 解き方
- 全体の重さは、次の式で表すことができる。
120 + 25 × 25 = 120 + 625 = 745 [g]
問2
4 個で 320 円の品物 A と、5 個で 200 円の品物 B があります。A 1 個の値段は B 1 個の値段の何倍ですか。
- 答え
- 2 倍
- 解き方
- 求めるのは、A 1 個の値段を B 1 個の値段でわった数なので、
( 320 ÷ 4 ) ÷ ( 200 ÷ 5 ) = 80 ÷ 40 = 2 [倍]
問3
えんぴつが 3 ダースと 8 本あります。これを 11 人で同じ数ずつ分けると、1人何本になりますか。
- 答え
- 4 本
- 解き方
- えんぴつの本数を人数でわった値が 1 人あたりの本数になる。えんぴつ 1 ダースは 12 本なので、
( 12 × 3 + 8 ) ÷ 11
= ( 36 + 8 ) ÷ 11
= 44 ÷ 11 = 4 [本]
問4
1 個 60 円のみかん 7 個と、1 個 180 円のりんごを 3 個買いました。代金は全部で何円になりましたか。
- 答え
- 960 円
- 解き方
- 代金は次の式で表すことができる。
60 × 7 + 180 × 3 = 420 + 540 = 960 [円]
問5
1 箱 98 円のチョコレートを 3 箱、1 袋 158 円のおせんべいを 2 袋、2 個で 189 円のお饅頭を 4 個買います。財布には 1 万円札しかありません。おつりはいくらになりますか。
- 答え
- 9012 円
- 解き方
- おつりは次の式で表すことができる。
10000 – { 98 × 3 + 158 × 2 + 189 × ( 4 ÷ 2 ) }
= 10000 – ( 294 + 316 + 378 ) = 9012 [円]
問6
みかんを何人かに分けるのに、1 人 5 個ずつ分けると 10 個あまり、1 人 7 個ずつ分けると 4 個足りません。みかんは全部で何個ありますか。
- 答え
- 45 個
- 解き方
- 【過不足算】
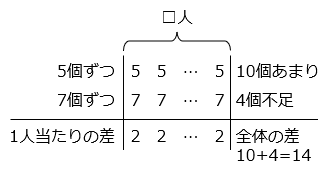
1 人あたりの差の 2 個が集まって 14 個の差になったので、みかんを分けた人数 (□) は、
14 ÷ 2 = 7 [人]
よって、みかんの個数は、
5 × 7 + 10 = 45 [個]
問7
n を 0 以上の整数とし、【n】は、n と 50 のうち大きい数から小さい数を引いた値を表すことにします。
(1)【5】を答えなさい。
- 答え(1)
- 45
- 解き方(1)
- 5 < 50 より、50 – 5 = 45
(2)【n】= 7 を満たす n をすべて答えなさい。
- 答え(2)
- 43, 57
- 解き方(2)
- n < 50 のとき、n = 50 – 7 = 43
n > 20 のとき、n = 50 + 7 = 57
(3)【n】+【n + 1】= 39 を満たす n をすべて答えなさい。
- 答え(3)
- 30, 69
- 解き方(3)
- 【n】+【n + 1】= 39 を満たす (【n】,【n + 1】) は ( 19, 20 ) または ( 20, 19 )
<【n】= 19 のとき>
n は 50 – 19 = 31 または 50 + 19 = 69
n = 31 のとき
【n + 1】=【32】= 50 – 32 = 18 ≠ 20
n = 69 のとき
【n + 1】=【70】= 70 – 50 = 20
<【n】= 20 のとき>
n は 50 – 20 = 30 または 50 + 20 = 70
n = 30 のとき
【n + 1】=【31】= 50 – 31 = 19
n = 70 のとき
【n + 1】=【71】= 71 – 50 = 21 ≠ 19
よって、n は 30 または 69
問8
1 日に 3 分の割合でおくれる時計があります。午前 8 時に正しい時刻にあわせたとき、その日の午後 10 時に、この時計は午後何時何分何秒をさしていますか。
- 答え
- 午後 9 時 58 分 15 秒
- 解き方
- 【差集め算】
1 日に 3 分の割合でおくれるということは、1 時間に 3 ÷ 24 = \(\dfrac{1}{8}\) [分] おくれることである。
午前 8 時からその日の午後 10 時までは 14 時間あるので、その間におくれる時間は、
\(\dfrac{1}{8}\) × 14 = \(1\dfrac{3}{4}\) [分] = 1 分 45 秒
よって、この時計がさしているのは午後 10 時の 1 分 45 秒前より、午後 9 時 58 分 15 秒
問9
正確な時計より 24 時間につき 4 分 15 秒進む時計と、正確な時計より 24 時間につき 2 分 45 秒おくれる時計があります。この 2 つの時計を昼 12 時に正確な時間に合わせました。その日の夜 12 時までのどこかで 2 つの時計を見ると、2 分 48 秒の差がありました。このときの正確な時刻は午後何時何分何秒ですか。
- 答え
- 午後 9 時 36 分 0 秒
- 解き方
- 【差集め算】
2 つの時計の差は 24 時間で 4 分 15 秒 + 2 分 45 秒 = 7 分 となる。すなわち、1 時間につき \(\dfrac{7}{24}\) 分 の差ができる。
2 分 48 秒 = \(2\dfrac{4}{5}\) 分の差ができるのにかかる時間は、
\(2\dfrac{4}{5}\) ÷ \(\dfrac{7}{24}\)
= \(\dfrac{14}{5}\) × \(\dfrac{24}{7}\)
= \(\dfrac{48}{5}\) = \(9\dfrac{3}{5}\) [時間] = 9 時間 36 分
したがって、正確な時間は昼 12 時の9 時間 36 分なので、午後 9 時 36 分 0 秒
問10
3 つの同じ 4 けたの数の足し算を筆算で計算したところ、下のようになりました。A ~ D に当てはまる 1 以上の 1 けたの整数をそれぞれ答えなさい。ただし、同じ文字には同じ数が入ります。
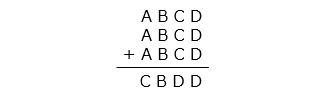
- 答え
- A:2 B:9 C:8 D:5
- 解き方
- 1 の位を考える。
D + D + D の 1 の位が D となるのは、D = 5 のとき。
よって、D + D + D = 5 + 5 + 5 = 15 となる。
10 の位を考える。
1 + C + C + C の 1 の位が D = 5 となる、すなわち C + C + C の 1 の位が 4 となるのは、 C = 8 のとき。
よって、1 + C + C + C = 1 + 8 + 8 + 8 = 25 となる。
100 の位を考える。
2 + B + B + B の 1 の位が B となる、すなわち B + B + B の 1 の位が B – 2 となるのは、 B = 4 または 9 のとき。
B = 4 のとき2 + B + B + B = 2 + 4 + 4 + 4 = 14 となる。
このとき、1000 の位を考える。
1 + A + A + A の 1 の位が C = 8 となる、すなわち A + A + A の 1 の位が 7 となる A は存在しない。よって、 B は 4 ではない。
B = 9 のとき2 + B + B + B = 2 + 9 + 9 + 9 = 29 となる。
このとき、1000 の位を考える。
2 + A + A + A の 1 の位が C = 8 となる、すなわち A + A + A の 1 の位が 6 となるのは、A = 2
問11
A、B には整数がはいります。<A, B>は A を B 回かけたときの一の位の数を表すものとします。例えば、3 × 3 × 3 × 3 = 81 なので、<3, 4> = 1 となります。
(1)<2, 10> の値を求めなさい。
- 答え(1)
- 4
- 解き方(1)
- 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 1024 より 4
※覚えておこう!
2 を 10 回かけた値は 1024
(2)<A, 1111> = <A, 1112>となる A は 1 から 30 までに何個ありますか。
- 答え(2)
- 12 個
- 解き方(2)
- 何回かけても 1 の位の数が等しくなる数は、1 の位が 0、1、5、6 の数
よって、1、5、6、10、11、15、16、20、21、25、26、30 の 12 個
問12
1 冊 130 円のノートを □ 冊買えるお金で 1 冊 70 円のノートを買ったところ、130 円のノートの冊数よりもちょうど 12 冊多く買えました。
□ にあてはまる数を答えなさい。
- 答え
- 14
- 解き方
- 【差集め算】
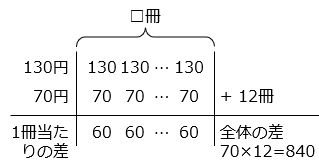
60 × □ = 840
□ = 840 ÷ 60 = 14 [冊]
問13
次の □ に、+、-、×、÷ のいずれかの記号を入れて、式を完成させなさい。
4 ÷ ( 1 \(\boxed{ア}\) 3 \(\boxed{イ}\) 5 ) = 10
- 答え
- ア:- イ:÷
- 解き方
- 4 ÷ ( 1 \(\boxed{ア}\) 3 \(\boxed{イ}\) 5 ) = 10
10 × ( 1 \(\boxed{ア}\) 3 \(\boxed{イ}\) 5 ) = 4
1 \(\boxed{ア}\) 3 \(\boxed{イ}\) 5 = \(\dfrac{4}{10}\) = \(\dfrac{2}{5}\)
分母に 5 がくることから、\(\boxed{イ}\) は ÷ と考えられる。
1 \(\boxed{ア}\) 3 ÷ 5 = 1 \(\boxed{ア}\) \(\dfrac{3}{5}\) = \(\dfrac{2}{5}\)
\(\boxed{ア}\) が – のとき、式は成り立つ。