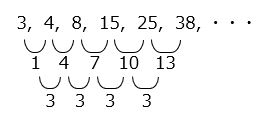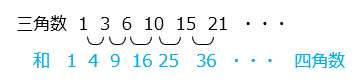算数【基本】数列

問１　等差数列

等差数列

となりどうしの数の差を「公差」、数列の初めの数を「初項」といい、公差の等しい数列を「等差数列」という。
（例）初項が1で公差が2の等差数列：1, 3, 5, 7, 9・・・

●n番目の数 = 初項 + 公差 × ( n – 1 )
●1番目からn番目までの数の和 = ( 1番目の数 + n番目の数 ) × n ÷ 2

（１）ある規則にしたがって、以下のように数が並んでいます。

3, 7, 11, 15, 19 ・・・

① 10番目の数を求めなさい。

答え（１）- ①

39

解き方（１）- ①

初項 = 3, 公差 = 4
n番目の数 = 初項 + 公差 × ( n – 1 ) より、
3 + 4 × ( 10 – 1 ) = 3 + 4 × 9 = 39

② 119は何番目の数ですか。

答え（１）- ②

30番目

解き方（１）- ②

n番目の数 = 初項 + 公差 × ( n – 1 ) より、
119 = 3 + 4 × ( n – 1 )
4 × ( n – 1 ) = 119 – 3
4 × n – 4 = 116
4 × n = 116 + 4
4 × n = 120
n = 30(番目)

（２）10から50までの整数の中で4で割って3余る数の和を求めなさい。

答え（２）

290

解き方（２）

10以上で4で割って3余る最も小さい数は11で、以降は4ずつ増加する。
よって、10から50までの整数の中で4で割って3余る数は、
11, 15, 19, 23, 27, 31, 35, 39, 43, 47
これは、初項が11、公差が4の等差数列の初項から10番目までの数の和と考えられる。
1番目からn番目までの数の和 = ( 1番目の数 + n番目の数 ) × n ÷ 2 より、
( 11 + 47 ) × 10 ÷ 2 = 58 × 10 ÷ 2 = 290

（３）次のA、Bはそれぞれある規則にしたがって数を並べています。AとBに共通してあらわれる数を小さい順に並べてできるCについて考えます。

A：8, 13, 18, 23, 28, 33, ・・・・・

B：15, 23, 31, 39, 47, 55, ・・・・・

A、Bに共通してあらわれる最初の数は23なので、Cの1番目の数は23です。

C：23, ・・・・・

① Cの5番目の数を求めなさい。

答え（３）- ①

183

解き方（３）- ①

Aは公差が5の等差数列、Bは公差が8の等差数列である。AとBに共通する数は、最初の23以降はAとBの公差の最小公倍数である40ごとにあらわれる。
よって、Cは初項が23、公差が40の等差数列になるので、5番目の数は、
23 + 40 × ( 5 – 1 ) = 183

② 583はCの何番目の数ですか。

答え（３）- ②

15番目

解き方（３）- ②

□番目の数とすると、
23 + 40 × ( □ – 1 ) = 583
40 × ( □ – 1 ) = 583 – 23
40 × □ – 40 = 560
40 × □ = 560 + 40
40 × □ = 600
□ = 600 ÷ 40 = 15(番目)

（４）ある規則にしたがって分数が並んでいます。

\(\dfrac{3}{4}\), \(\dfrac{5}{6}\), \(\dfrac{7}{8}\), \(\dfrac{9}{10}\), ・・・

分母と分子の和が151になるのは何番目ですか。

答え（４）

37番目

解き方（４）

分母と分子の和は、7, 11, 15, 19, ・・・となる。
この等差数列の□番目が151になるのは、
7 + 4 × ( □ – 1 ) = 151
4 × □ = 148
□ = 37

（５）ある規則にしたがって数が並んでいます。

50, 50, 49, 50, 49, 48, 50, 49, 48, 47, ・・・

① はじめて1があらわれるのは、最初から数えて何番目ですか。

答え（５）- ①

1275番目

解き方（５）- ①

図のように50を基準に区切ると、新たな規則が見えてくる。群の数と、各群の数の個数は同じである。
はじめて1があらわれるのは、50 ～ 1 の50個の数が並ぶ50群の50番目である。
50群の50番目の全番数は、すべての数の全個数に等しい。
各群の数の個数は、初項1、公差1の等差数列になっているので、
( 1 + 50 ) × 50 ÷ 2 = 1275(番目)

② 最初から数えて50番目の数を求めなさい。

答え（５）- ②

46

解き方（５）- ②

1群から9群までの数の個数は、1 + 2 + ・・・ + 9 = ( 1 + 9 ) × 9 ÷ 2 = 45(個)より、最初から数えて50番目の数は、10群の5番目の数である。
よって、「50, 49, 48, 47, 46, ・・・」
※「1 + 2 + ・・・ + 9 = 45」、「1 + 2 + ・・・ + 9 + 10 = 55」は覚えておくと便利です。

（６）Aが1より大きいの整数のとき、＜A＞はAを分母にもち、分子が1からAまでの分数をすべて足した数をあらわします。

例えば、

＜2＞= \(\dfrac{1}{2}\) + \(\dfrac{2}{2}\) =\(\dfrac{3}{2}\)

＜3＞= \(\dfrac{1}{3}\) + \(\dfrac{2}{3}\) + \(\dfrac{3}{3}\) = 2

＜4＞= \(\dfrac{1}{4}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{4}\) + \(\dfrac{4}{4}\) = \(\dfrac{5}{2}\)

① ＜17＞を求めなさい。

答え（６）- ①

9

解き方（６）- ①

＜17＞ = \(\dfrac{1}{17}\) + \(\dfrac{2}{17}\) + ・・・ + \(\dfrac{17}{17}\)

= \(\dfrac{1\ +\ 2\ +\ ・・・\ +\ 17}{17}\)

= \(\dfrac{(1\ +\ 17)\ ×\ 17\ ÷\ 2}{17}\)

= \(\dfrac{18\ ×\ 17\ ÷\ 2}{17}\) = 9

【別解】
<1>, <2>, <3>, <4>, , , を、
1, 1.5, 2, 2.5, , ,の数列とすると
初項：1, 公差：0.5の17番目の数を求めると
1 + 0.5 × ( 17 – 1 ) = 9

② ＜2＞, ＜3＞, ・・・ ＜1000＞までの数のうち、整数は何個ありますか。

答え（６）- ②

499個

解き方（６）- ②

<1>, <2>, <3>, <4>, , , を、
1, 1.5, 2, 2.5, , ,の数列として考えると、
<奇数>の場合は整数になる。
よって、<2>から<1000>までのうち奇数は、500 – 1 = 499(個)

【別解】
1より大きいある整数を□とすると、

＜□＞ = \(\dfrac{1}{□}\) + \(\dfrac{2}{□}\) + ・・・ + \(\dfrac{□}{□}\)

= \(\dfrac{(1\ +\ □)\ ×\ □\ ÷\ 2}{□}\) = ( 1 + □ ) ÷ 2

よって、1 + □ が偶数、すなわち□が奇数のとき、＜□＞は整数となる。
2から1000のうち奇数は499個。

（７）図のように85個のご石がある規則にしたがって並んでいます。

●●●○●●●○○●●●○○○●●●○○○○●●●○○・・・

① 黒いご石は何個ありますか。

答え（７）- ①

30個

解き方（７）- ①

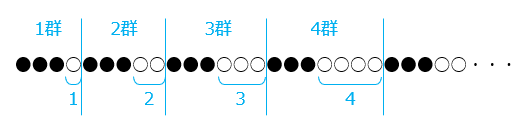
黒いご石を基準に区切り、白いご石の個数に注目すると、1、2、3、4・・・と規則的な並びになっている。
10群まであると仮定した場合、白いご石の個数は55個
黒いご石は各群に3個ずつあるので、30個
合わせて 55 + 30 = 85(個)となるので、黒いご石は 30個

② 白いご石のうち、左から25番目にあるものは、全体では左から何番目ですか。

答え（７）- ②

46番目

解き方（７）- ②

1 + 2 + 3 + 4 + 5 + 6 = 21、1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 より、白いご石の25番目は7群にある。よって全体では、
3 × 7 + 25 = 46(番目)

（８）ある規則にしたがって数が並んでいます。420より小さくなるのは、はじめから数えて何番目ですか。

554, 542, 530, 518, ・・・

答え（８）

13番目

解き方（８）

順に12ずつ小さくなっている。
554 – 420 = 134
134 ÷ 12 = 11 あまり 2

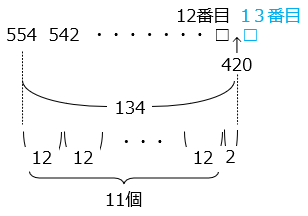
はじめから数えるので12番目から13番目の間に420がある。
よって、13番目。

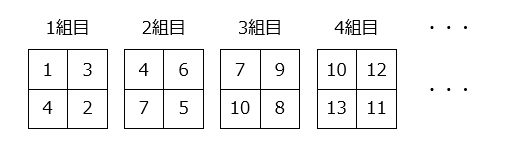
（９）ある規則にしたがって、数が図のような組になって並んでいます。1000がはじめてあらわれるのは何組目ですか。

答え（９）

333番目

解き方（９）

各組は4つの連続した数で、1000は4で割り切れるので、1000は左下にある。
各組の左下の数は、
4, 7, 10, 13, ・・・
初項が4、公差が3の等差数列になっている。よって、1000がはじめてあらわれるのが□組目とすると、
4 + 3 × ( □ – 1 ) = 1000
4 + 3 × □ – 3 = 1000
3 × □ = 1000 + 3 – 4
3 × □ = 999
□ = 333(番目)

問２　階差数列

階差数列

数列の差も数列となるとき、その差の数列を「階差数列」という。このとき、元の数列のn番目の数は、初項に ( n – 1 ) 個の階差数列の和を加えた値になる。
（例）階差数列が等差数列の場合

（１）ある規則にしたがって数が並んでいます。10番目の数を求めなさい。

3, 4, 8, 15, 25, 38, ・・・

答え（１）

120

解き方（１）

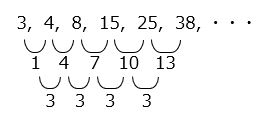
となり合った数の差は、初項が1、公差3の等差数列になっている。
10番目の数は、初項3と等差数列(1, 4, 7…)の1から9番目(10 – 1)までの数の和を足した数になる。
等差数列の9番目は
初項 + 公差 × ( n – 1 )より
1 + 3 × ( 9 – 1 ) = 25
よって10番目の数は、
3 + {( 1 + 25 ) × 9 ÷ 2 }
= 3 + 117
= 120

（２）ある規則にしたがって、図のように数が並んでいます。

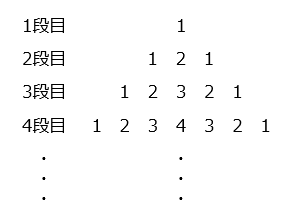
① 5段目に含まれる数は何個ありますか。

答え（２）- ①

9個

解き方（２）- ①

5段目の数は、「1、2、3、4、5、4、3、2、1」の9個

② 5段目に含まれる数の合計を求めなさい。

答え（２）- ②

25

解き方（２）- ②

1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1
= ( 1 + 2 + 3 + 4 ) + 5 + ( 4 + 3 + 2 + 1 )
= 10 + 5 + 10 = 25

③ 100段目に含まれる数の合計を求めなさい。

答え（２）- ③

10000

解き方（２）- ③

各段に含まれる数の合計は、差が初項3、公差2の等差数列になっている。
等差数列の99番目の数は、
3 + 2 × ( 99 – 1 ) = 199
100段目に含まれる数の合計は、
1 + {( 3 + 199 ) × 99 ÷ 2 }
= 1 + ( 202 × 99 ÷ 2 )
= 1 + ( 202 × 99 ÷ 2 )
= 1 + 9999 = 10000

【別解】四角数（下記の問３参照）
各段に含まれる数の合計は、1から始まる連続した奇数の和となる
1, 4(= 1 + 3), 9(= 1 + 3 + 5), 16(= 1 + 3 + 5 + 7), ・・・
⇒ 四角数
各段に含まれる数の合計は平方数の並びである
1(= 1 × 1), 4(= 2 × 2), 9(= 3 × 3), 16(= 4 × 4), ・・・
⇒ 四角数
各段に含まれる数の合計が四角数であると気づけば、100段目の合計は 100 × 100 = 10000

問３　三角数・四角数

三角数・四角数

三角数：点を正三角形の形状に並べたとき、その点の総数を「三角数」という。三角数は、1から始まる連続した整数の和となる。

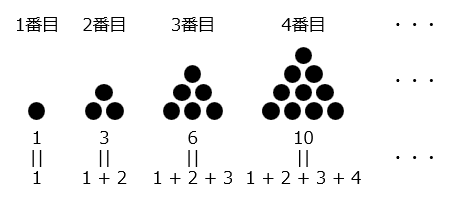
●n番目の三角数 = ( 1 + n ) × n ÷ 2

四角数：点を正方形の形状に並べたとき、その点の総数を「四角数」という。四角数は平方数（同じ整数を2回かけてできる数）であり、1から始まる連続した奇数の和となる。

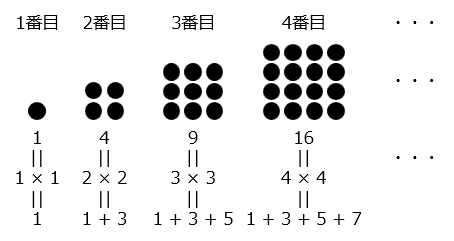
●n番目の四角数 = n × n

●三角数のとなりどうしの和 = 四角数

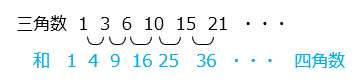
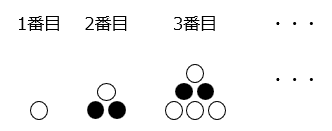
（１）白と黒のご石をある規則にしたがって並べました。

① 7番目ではご石は何個ですか。

答え（１）- ①

28個

解き方（１）- ①

ご石の個数は、順に1、3、6・・(個)となっている。
これは三角数である。
よって7番目の個数は、( 1 + 7 ) × 7 ÷ 2 = 28(個)

② ７番目では白のご石は何個ですか。

答え（１）- ②

16個

解き方（１）- ②

番数と上から数えた段数は同じで、各段数とご石の数は同じである。
すなわち7番目の段数は7段で、白のご石は奇数段なので、
1 + 3 + 5 + 7 = 16(個)

③ 黒のご石の方が、白のご石より20個多くなるのは何番目ですか。

答え（１）- ③

40番目

解き方（１）- ③

黒のご石の方が、白のご石より多くなるのは、段数が偶数のときである。そして、黒のご石は、前の段の白のご石の個数より1個多くなっている。
1番目：白1, 黒0
2番目：白1, 黒2
3番目：白4, 黒2
4番目：白4, 黒6
5番目：白9, 黒6
6番目：白9, 黒12
段数が偶数のとき、黒 – 白の個数□を求めると、
□ × 2 が段数の数となる。
よって、
20 × 2 = 40(番目)

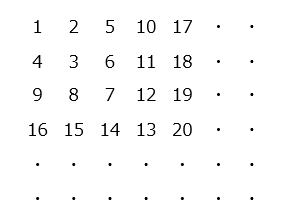
（２）ある規則にしたがって数が並んでいます。

① 上から15段目の左から1列目の数を求めなさい。

答え（２）- ①

225

解き方（２）- ①

一番左の数を1段目から並べると、
1(= 1 × 1), 4(= 2 × 2), 9(= 3 × 3), 16(= 4 × 4), ・・・
これは四角数の並びである。よって15段目の数は、
15 × 15 = 225

② 84は上から何段目の左から何列目にありますか。

答え（２）- ②

上から3段目の左から10列目

解き方（２）- ②

84に最も近い平方数は 9 × 9 = 81
81は9段目の1列目の数である。

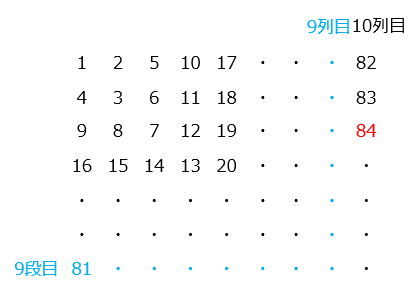
図より、上から3段目の左から10列目

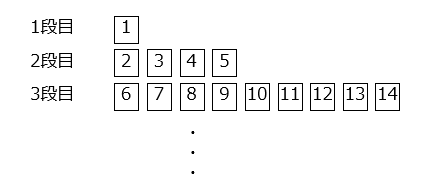
（３）ある規則にしたがって、図のように1から100の整数が書かれたカードを並べます。すべてのカードを並べるためには何段必要ですか。

答え（３）

7段

解き方（３）

1段目から順に各段のカードの枚数は、1枚、4枚、9枚、・・・と四角数になっている。各段の右はしのカードの整数（最も大きい整数）は、そのカードまでの全枚数になっている。各段のカードの枚数を1段目から順に足していくと、
1 + 4 + 9 + 16 + 25 + 36 = 91（6段目の右はしの数）
1 + 4 + 9 + 16 + 25 + 36 + 49 = 140（7段目の右はしの数）
よって、7段。