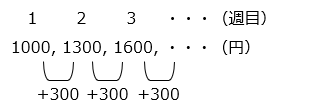算数【応用】数列

問１

A さんは新しいタブレットを買うために目標金額を決め、貯金することにしました。1 週目は 1000 円、2 週目は 1300 円、3 週目は 1600 円、・・・というように前の週よりも 300 円ずつ多く貯金したところ、14 週目で貯金額の合計と目標金額が等しくなりました。目標金額は何円ですか。

答え: 41300 円

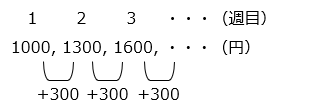
解き方: 貯金額は、初項 1000、公差 300 の等差数列になっている。よって、14 週目の貯金額は、
1000 + 300 × ( 14 – 1 ) = 4900 [円]
目標金額は 14 週目までの貯金額の合計なので、
14 × ( 1000 + 4900 ) ÷ 2 = 41300 [円]

問２

図のように数を並べます。

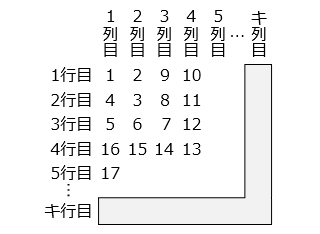
（１）□ に当てはまる数を答えなさい。

① 5 行目 5 列目の数は \(\boxed{ア}\) です。

答え（１）- ①: ア：21

解き方（１）- ①: 1 行目 1 列、2 行目 2 列、3 行目 3 列、・・・の数をぬき出すと、各数の差は初項 2、公差 2 の等差数列になっている。
よって、5 行目 5 列目の数は 13 + 8 = 21

② 81 は、 \(\boxed{イ}\) 行目 \(\boxed{ウ}\) 列目の数です。100 は、 \(\boxed{エ}\) 行目 \(\boxed{オ}\) 列目の数です。

答え（１）- ②: イ：1　ウ：9　エ：10　オ：1

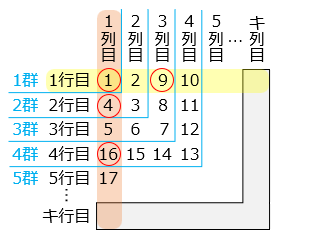
解き方（１）- ②: 図のように群に分けると、各群の最大の数 (○) は四角数となっている。
81 = 9 × 9 より、9 群の最大の数である。
奇数の群の最大の数は 1 行目に位置することから、81 は 1 行目 9 列目の数となる。

100 = 10 × 10 より、10 群の最大の数である。
偶数の群の最大の数は 1 列目に位置することから、100 は 10 行目 1 列目の数となる。

③ 1215 は \(\boxed{カ}\) 行目 \(\boxed{キ}\) 列目の数です。

答え（１）- ③: カ：11　キ：35

解き方（１）- ③: 1215 は □ 群に含まれるとすると、
□ × □ ≧ 1215
34 × 34 = 1156 ＜ 1215 ⇒ ×
35 × 35 = 1225 ＞ 1215 ⇒ ○
よって、1215 は 35 群に含まれる。
1225 は 35 群の最大の数なので 1 行目 35 列目、1225 – 1215 = 10 より、1215 は　1 + 10 = 11 [行目] となる。よって、11 行 35 列目。

（２）図の \(\boxed{キ}\) 行目 \(\boxed{キ}\) 列目のかげのついた部分にある整数の和を求めなさい。

答え（２）: 82179

解き方（２）: 求めるのは 35 群の数の和。
35 群の最初の数は 34 × 34 + 1 = 1157、最後の数は 1225
35 群の数の個数は、1225 – 1157 + 1 = 69 [個]
よって、35 群の数の和は、
69 × ( 1157 + 1225 ) ÷ 2 = 82179

問３

ある規則に従って、次のように左から数字が並んでいます。

1, 1, 3, 1, 3, 5, 1, 3, 5, 7, 1, 3, 5, 7, 9, ・・・

このとき、左から 50 番目の数字は何ですか。

答え: 9

解き方: 各群の数字の個数は初項 1、公差 1 の等差数列になっている。
1 群から 9 群までの数字の個数の和は 45 より、50 番目の数は 10 群の左から 5 番目の数字である。
また、各群の数字は左から初項 1、公差 2 の等差数列になっている。したがって、10 群の左から 5 番目の数字は、
1 + 2 × ( 5 – 1 ) = 9

問４

（１）次の数字の列はある規則に従って並んでいます。

1, \(\dfrac{1}{2}\), \(\dfrac{1}{4}\), \(\dfrac{1}{8}\), \(\dfrac{1}{16}\), \(\dfrac{1}{32}\), ・・・

このとき、10 番目の数字は何ですか。

答え（１）: \(\dfrac{1}{512}\)

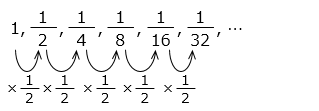
解き方（１）: 右の数は、前の数に \(\dfrac{1}{2}\) をかけた数である。
よって、10 番目の数は 1 に \(\dfrac{1}{2}\) を 9 個かけた値となる。
1 × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\)
= 1 × \(\dfrac{1}{2\ ×\ 2\ ×\ 2\ ×\ 2\ ×\ 2\ ×\ 2\ ×\ 2\ ×\ 2\ ×\ 2}\)
= \(\dfrac{1}{512}\)

※覚えておこう！
2 を 10 回かけた値は 1024
( 2 を 9 回かけた値は 1024 ÷ 2 = 512 )

（２）（１）で並んでいる数字を前から順番に足す、つまり

1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + ・・・

を計算すると、その和はいくつになりそうですか。①～⑥から 1 つ選び、それを選んだ理由を説明しなさい。

①　1.5

②　2

③　2.5

④　3

⑤　4

⑥　とにかく大きくなる

なお、説明するときには下の正方形を使っても構いません。

答え（２）: ②

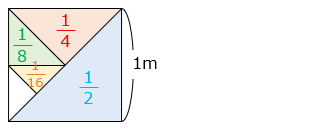
解き方（２）: 正方形の面積を 1 とし、その正方形を \(\dfrac{1}{2}\)、\(\dfrac{1}{4}\)、・・・の面積の直角二等辺三角形で順に埋めていくと考える。
すると、必ず新たに埋めた面積と同じ面積が残ってしまう。したがって、
\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + ・・・
は、限りなく 1 に近づくが、決して 1 にはならない。
また、1.5 = 1 + 0.5 = 1 + \(\dfrac{1}{2}\) より、
1.5 ＜ 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + ・・・＜ 2

問５

次のように分数がある規則に従って並んでいます。

\(\dfrac{1}{1}\), \(\dfrac{1}{2}\), \(\dfrac{2}{2}\), \(\dfrac{1}{3}\), \(\dfrac{2}{3}\), \(\dfrac{3}{3}\), \(\dfrac{1}{4}\), \(\dfrac{2}{4}\), \(\dfrac{3}{4}\), \(\dfrac{4}{4}\), \(\dfrac{1}{5}\), \(\dfrac{2}{5}\),\(\dfrac{3}{5}\), ・・・

（１）はじめから数えて85 番目の数は何ですか。

答え（１）: \(\dfrac{7}{13}\)

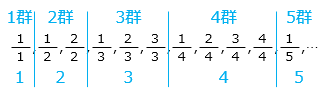
解き方（１）: 各群の番号と、分子の数字、要素の個数は等しい。各群の数の個数は初項 1、公差 1 の等差数列になっている。
1 群から 10 群までの数の個数の和は 55 である。
55 + 11 + 12 = 78
55 + 11 + 12 + 13 = 91
よって、85 番目の数は 13 群の 7 番目の数より、 \(\dfrac{7}{13}\)

（２）\(\dfrac{17}{21}\) ははじめから数えて何番目の数ですか。

答え（２）: 227 番目

解き方（１）: \(\dfrac{17}{21}\) は 21 群の 17 番目の数である。
1 群から 20 群までの数の個数の和は、
20 × ( 1 + 20 ) ÷ 2 = 210
よって、210 + 17 = 227 [番目]

問６

ある規則に従って、次のように数の入った図形をつくることにしました。

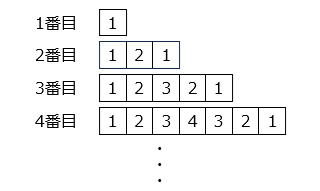
（１）8 番目の図形に入っている数の和から 7 番目に入っている数の和を引いた値を求めなさい。

答え（１）: 15

解き方（１）: 共通の数を除き、残った数を足す。
8 + 7 = 15

（２）15 番目の図形に入っている数の和から 10 番目に入っている数の和を引いた値を求めなさい。

答え（２）: 125

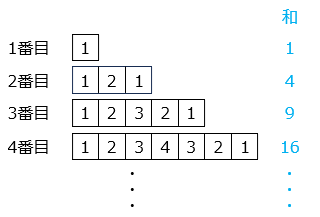
解き方（２）: 各図形に入っている数の和は平方数になっていることから、
15 番目の図形に入っている数の和は 15 × 15 = 225
10 番目の図形に入っている数の和は 10 × 10 = 100
よって、225 – 100 = 125

（３）50 番目の図形に入っている数の和を求めなさい。

答え（３）: 2500

解き方（３）: 50 × 50 = 2500