算数【基本】濃度(食塩水)
- 食塩水濃度計算まとめ表(気に入ったら使ってください)
- この表は本サイトが推奨する方法です。
表には次のように値を入れます。
| 食塩 | 水 |
| 濃度[%] | 食塩の割合 | 水の割合 |
| 量[g] | 食塩の量 | 水の量 |
| 食塩水の量[g] | 食塩水 |
それでは、実際に使ってみましょう。
10 % の食塩水が 200 g あります。食塩水中に含まれている水の量 [g]を求めなさい。
まずは問題文から表に数値を入れます。
※表は漢字の「目」を書いて、縦棒を 1 本書くと簡単に書けます。問題を読み取り数字を入れたら、白色の空らんのところを計算してみましょう。
まずは右上の水の割合は、全体で 100 % なので、100 – 10 = 90 [%]
食塩水 200 g の 90 % が水なので、200 × 0.9 = 180 [g] となります。
さらに食塩の量は、食塩水 200 g の 10 %なので、20 gとわかります。
表に数字を当てはめると、となりました。簡単でしょ!!
この表は 5 個のわくがありますが、少なくとも 1 つ量 [g] の数値がわかっていて、5 個のわくのうち 2 個数値があればすべて計算で求めることができます。
問1
(1)濃度 16 % の食塩水 250 g の中に含まれている水は何 g ですか。
- 答え(1)
- 210 g
- 解き方(1)
- 問題文から水の割合は、100 – 16 = 84 [%]なので、
250 × 0.84 = 210 [g]
(2)180 g の水に 20 g の食塩を混ぜると、できる食塩水の濃度は何 % ですか。
- 答え(2)
- 10 %
- 解き方(2)
- 問題文から食塩水の量は、20 + 180 = 200 [g]
食塩水の濃度は、20 ÷ 200 × 100 = 10 [%]
(3)8 % の食塩水 150 g の中に含まれる食塩の量は何 g ですか。
- 答え(3)
- 12 g
- 解き方(3)
- 問題文から150 × 0.08 = 12 [g]
(4)食塩を 2.5 g含む、10 gの食塩水の濃度は何 % ですか。
- 答え(4)
- 25 %
- 解き方(4)
- 問題文から2.5 ÷ 10 × 100 = 25 [%]
(5)5 % の食塩水 200 g に入っている食塩の量が、ある濃度の食塩水 500 g に入っている食塩の量と同じとき、ある濃度は何 % ですか。
- 答え(5)
- 2 %
- 解き方(5)
- 問題文から5 % の食塩水 200 g に入っている食塩の量は、200 × 0.05 = 10 [g]
10 g の食塩を含む食塩水 500 g の濃度を求める。10 ÷ 500 × 100 = 2 [%]
問2
- ヒント
- ●水の増減によって食塩水の量は変化するが、食塩の量は変化しない。
●食塩の量が増えると、その分食塩水の量も増える。
●食塩水の増減は、食塩水の量および食塩の量の両方が変化する。
(1)8 % の食塩水 200 g に水 300 g を加えると、何 % の食塩水になりますか。
- 答え(1)
- 3.2 %
- 解き方(1)
- 問題文より 300 g 水を加える前の数値は表のように計算できる。
次に水を 300 g 加えた表を書く。
このとき量が変化したので割合の数値は変わるが、食塩の量は変化がないので 16 g のままである。16 ÷ 500 × 100 = 3.2 [%]
(2)6 % の食塩水 200 g から、水を 50 g 蒸発させました。できた食塩水の濃度は何 % ですか。
- 答え(2)
- 8 %
- 解き方(2)
- 問題文より 50 g の水を蒸発させる前の数値は表のように計算できる。
次に水を 50 g 蒸発させた(減った)表を書く。
このとき量が変化したので割合の数値は変わるが、食塩の量は変化がないので 12 g のままである。
12 ÷ 150 × 100 = 8 [%]
(3)濃度 15 % の食塩水 400 g に何 g の水を加えると、濃度 6 % の食塩水になりますか。
- 答え(3)
- 600 g
- 解き方(3)
- 問題文より水を加える前と後を表で表す。
水を加える前は
水を加えた後は、食塩 60 g の量は変化しないので、
60 g の食塩を含む 6 % の食塩水の量は、60 ÷ 0.06 = 1000 [g]
よって、加える水の量は、1000 – 400 = 600 [g]
【別解】面積図をかく
縦を濃度 [%]、横を食塩水の量とすると、面積の大きさが食塩の量となる。
加えた水の量を □ g とする。
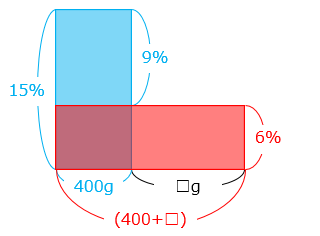
面積図より青色と赤色の面積は同じなので、
9 × 400 = 6 × □
□ = 600 [g]
(4)食塩水 300 g に水 150 g を加えると、4 % の食塩水になりました。水を加える前の食塩水の濃度は何 % ですか。
- 答え(4)
- 6 %
- 解き方(4)
- 問題文より水を加える前と後を表にする。
今回は、水を加えた後から考える。
水を加えることで、4 % の食塩水が 300 + 150 = 450 [g] できたということなので、含まれる食塩の量は、450 × 0.04 = 18 [g]
水を加える前は、食塩水の量は異なるが、食塩の量は同じなので、
18 ÷ 300 × 100 = 6 [%]
(5)3 % の食塩水 500 g から水を何 g か蒸発させたら、5 % の食塩水ができました。何 g の水を蒸発させたか答えなさい。
- 答え(5)
- 200 g
- 解き方(5)
- 問題文より水を蒸発させる前と後を表にする。
水を蒸発させる前
3 % の食塩水 500 g に含まれる食塩の量は、500 × 0.05 = 15 [g]
水を蒸発させた後は、食塩水の量は減るが、食塩の量は変化しない。
15 g の食塩を含む 5 % の食塩水の量は、15 ÷ 0.05 = 300 [g]
よって、蒸発させた水の量は、500 – 300 = 200 [g]
【別解】面積図をかく
縦を濃度 [%]、横を食塩水の量とすると、面積の大きさが食塩の量となる。
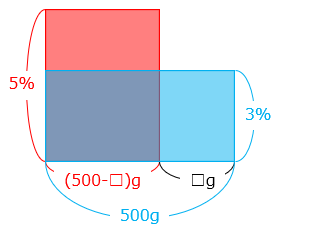
蒸発させた水の量を □ g とすると、青色と赤色の面積は同じなので、
3 × 500 = 5 × ( 500 – □ )
1500 = 2500 – 5 × □
5 × □ = 2500 – 1500 = 1000
□ = 200 [g]
(6)5 % の食塩水 200 g に食塩 50 g を加えたら、何 % の食塩水ができますか。
- 答え(6)
- 24 %
- 解き方(6)
- 問題文より食塩を加える前と後を表にする。
食塩を加える前
5 % の食塩水 200 g に含まれる食塩の量は、200 × 0.05 = 10 [g]
食塩を加えた後
食塩を加えたら、水の量は変化しないが、食塩水の量は増える。
60 ÷ 250 × 100 = 24 [%]
(7)7 % の食塩水 300 g と 12 % の食塩水 200 g を混ぜ合わせると何 % の食塩水になりますか。
- 答え(7)
- 9 %
- 解き方(7)
- それぞれの食塩水を表にする。
7 % の食塩水 300 g
含まれる食塩の量は、300 × 0.07 = 21 [g]
12 % の食塩水 200 g
含まれる食塩の量は、200 × 0.12 = 24 [g]
2 つの食塩水を混ぜ合わせた食塩水
⇒ 量の部分を足す(濃度は足せません)
食塩の量 21 + 24 = 45 [g]、食塩水の量 300 + 200 = 500 [g]
45 ÷ 500 × 100 = 9 [%]
(8)1 % の食塩水 200 g と 3 % の食塩水 300 g と 5 % の食塩水 500 g を加えると、何 % の食塩水になりますか。
- 答え(8)
- 3.6 %
- 解き方(8)
- それぞれの食塩水を表にする。
1 % の食塩水 200 g
含まれる食塩の量は、200 × 0.01 = 2 [g]
3 % の食塩水 300 g
含まれる食塩の量は、300 × 0.03 = 9 [g]
5 % の食塩水 500 g
含まれる食塩の量は、500 × 0.05 = 25 [g]
3 つの食塩水を混ぜ合わせた食塩水
⇒ 量の部分を足す(濃度は足せません)
食塩の量 2 + 9 + 25 = 36 [g]、食塩水の量 200 + 300 + 500 = 1000 [g]
36 ÷ 1000 × 100 = 3.6 [%]
(9)6 % の食塩水 500 g とある濃度の食塩水 200 g を混ぜると、10 % の食塩水になりました。加えた食塩水の濃度は何 % ですか。
- 答え(9)
- 20 %
- 解き方(9)
- それぞれの食塩水を表にする。
2 つの食塩水を混ぜ合わせた食塩水
10 % の食塩水が 500 + 200 = 700 [g] できたということなので、含まれる食塩の量は、700 × 0.1 = 70 [g]
6 % の食塩水 500 g
含まれる食塩の量は、500 × 0.06 = 30 [g]
ある濃度の食塩水 200 g
含まれる食塩の量は、混ぜてできた食塩水に含まれる食塩の量から、6 % の食塩水に含まれる食塩の量を引いた値なので、70 – 30 = 40 [g]
40 ÷ 200 × 100 = 20 [%]
【別解】面積図をかく
縦を濃度 [%]、横を食塩水の量とすると、面積の大きさが食塩の量となる。
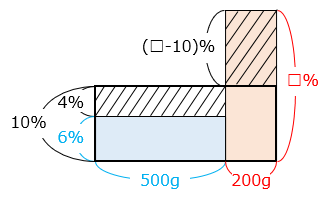
ある濃度を □ % とすると、斜線部分の面積が等しくなるので、
( □ – 10 ) × 200 = 4 × 500
200 × □ – 2000 = 2000
200 × □ = 2000 + 2000 = 4000
□ = 20 [%]
(10)3 % の食塩水 200 g と 6 % の食塩水を混ぜると 5 % の食塩水ができました。加えた 6 % の食塩水は何 g ですか。
- 答え(10)
- 400 g
- 解き方(10)
- それぞれの食塩水を表にする。
① 3 % の食塩水 200 g
含まれる食塩の量は、200 × 0.03 = 6 [g]
② 5 % の食塩水
③ 6 % の食塩水
食塩の量、食塩水の量はそれぞれ ② から ① の量を引けばよいが、② の量の情報がないのでどちらも求められない。
③ の食塩水について、表を埋める計算をするために必要な量 [g] の情報が 1 つもない ⇒ 表からは答えを出すことができない。
この場合は、面積図を利用する。
2 種類の食塩水を混ぜ合わせるということは、濃度の高いものと低いものを平均化すると考えられる。
縦を濃度 [%]、横を食塩水の量とすると、面積の大きさが食塩の量となる。

加えた6 % の食塩水を □ g とすると、斜線部分の面積が等しくなるので、
1 × □ = 2 × 200
□ = 400 [g]
(11)5 % の食塩水 200 g と 12 % の食塩水 300 g を混ぜ合わせたあとに、この食塩水から水を 100 g 蒸発させました。できた食塩水の濃度は何 % ですか。
- 答え(11)
- 11.5 %
- 解き方(11)
- それぞれの食塩水を表にする。
5 % の食塩水 200 g
含まれる食塩の量は、200 × 0.05 = 10 [g]
12 % の食塩水 300 g
含まれる食塩の量は、300 × 0.12 = 36 [g]
2 つの食塩水を混ぜ合わせた食塩水
⇒ 量の部分を足す(濃度は足せません)
食塩の量 10 + 36 = 46(g)、食塩水の量 200 + 300 = 500 [g]
混ぜた後、水を100g蒸発させた食塩水
食塩の量は変化しないが、蒸発させた分食塩水の量は減るので、500 – 100 = 400(g)
46 ÷ 400 × 100 = 11.5 [%]
(12)8 % の食塩水 200 g から、水を 50 g 蒸発させ、4 % の食塩水 50 g を混ぜたとき、できる食塩水の濃度は何 % ですか。
- 答え(12)
- 9 %
- 解き方(12)
- それぞれの食塩水を表にする。
① 8 % の食塩水 200 g
含まれる食塩の量は、200 × 0.08 = 16 [g]
② 水を 50 g 蒸発させた食塩水
食塩の量は変化しないが、蒸発させた分食塩水の量は減るので、200 – 50 = 150 [g]
③ 4 % の食塩水 50 g
含まれる食塩の量は、50 × 0.04 = 2 [g]
② と ③ の食塩水を混ぜ合わせた食塩水
⇒ 量の部分を足す(濃度は足せません)
食塩の量 16 + 2 = 18 [g]、食塩水の量 150 + 50 = 200 [g]
18 ÷ 200 × 100 = 9 [%]
(13)13 % の食塩水と 8 % の食塩水を混ぜて、10 % の食塩水を 500 g 作りました。13 % の食塩水は、何 g 混ぜましたか。
- 答え(13)
- 200 g
- 解き方(13)
- それぞれの食塩水を表にする。
① 8 % の食塩水
② 10 % の食塩水 500 g
含まれる食塩の量は、500 × 0.1 = 50 [g]
③ 13 % の食塩水
食塩の量、食塩水の量はそれぞれ ② から ① の量を引けばよいが、② の量の情報がないのでどちらも求められない。
③ の食塩水について、表を埋める計算をするために必要な量 [g] の情報が 1 つもない ⇒ 表からは答えを出すことができない。
この場合は、面積図を利用する。
2 種類の食塩水を混ぜ合わせるということは、濃度の高いものと低いものを平均化すると考えられる。
縦を濃度 [%]、横を食塩水の量とすると、面積の大きさが食塩の量となる。
13 % の食塩水を □ g とする。
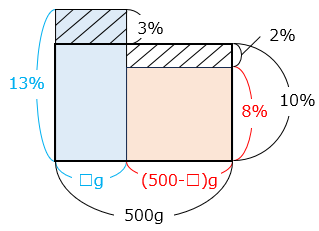
斜線部分の面積が等しくなるので、
3 × □ = 2 × ( 500 – □ )
3 × □ = 1000 – 2 × □
3 × □ + 2 × □ = 1000
5 × □ = 1000
□ = 200 [g]
【別解】つるかめ算を利用する
すべて 8 % の食塩水で 500 g 作ったとすると、食塩の量は 500 × 0.08 = 40 [g] となる。ただし、実際の食塩の量は 500 × 0.1 = 50 [g] である。
よって 13 % の食塩水の量は、
( 50 – 40 ) ÷ ( 0.13 – 0.08 ) = 10 ÷ 0.05 = 200 [g]
※全体の食塩の量の差を、1 g あたりの食塩の量の差で割る。
(14)12 % の食塩水があります。これを蒸発させたら 18 % の食塩水が 300 g できました。はじめの食塩水は何 g でしたか。
- 答え(14)
- 450 g
- 解き方(14)
- それぞれの食塩水を表にする。
18 % の食塩水 300 g
含まれる食塩の量は、300 × 0.18 = 54 [g]
12 % の食塩水
水を蒸発させる前後で食塩の量は変化しない。
54 ÷ 0.12 = 450 [g]
問3
(1)320 g の水に食塩を 80 g 溶かして食塩水を作りました。そこから 25 g を捨て、水を何 g か加えて 15 % の食塩水にしました。
① 捨てた食塩水に含まれていた食塩は何 g ですか。
- 答え(1)- ①
- 5 g
- 解き方(1)- ①
- はじめにできた食塩水
濃度は、80 ÷ 400 × 100 = 20 [%]
よって、捨てた食塩水に含まれていた食塩は、
25 × 0.2 = 5 [g]
② 加えた水は何 g ですか。
- 答え(1)- ②
- 125 g
- 解き方(1)- ②
- 25 g を捨てたときの食塩水
含まれている食塩の量は 80 – 5 = 75 [g]、食塩水の量は 400 – 25 = 375 [g]
水を加えてできた食塩水
水を加える前後で食塩の量は変化しないが、食塩水は加えた水の量増える。
食塩水の量は、75 ÷ 0.15 = 500 [g]
よって、加えた水の量は、500 – 375 = 125 [g]
(2)容器 A には 15 % の食塩水が 400 g、容器 B には 7 %の食塩水が 100 g 入っています。まず、容器 A から食塩水 100 g をとって、それを容器 B に入れてよくかき混ぜます。次に、容器 B から食塩水 100 g をとって、それを容器 A に入れてよくかき混ぜます。このとき、容器 A の食塩水の濃度は何 % ですか。
- 答え(2)
- 14 %
- 解き方(2)
- ①:はじめの容器 A
含まれている食塩の量は 400 × 0.15 = 60 [g]
そのうち 100 g に含まれていた食塩の量は 60 × \(\dfrac{100}{400}\) = 15 [g]
②:食塩水 100 g を取ったあとの容器Aの食塩水を表にすると、
③:はじめの容器 B
含まれている食塩の量は、100 × 0.07 = 7 [g]
④:① ( 容器 A ) から食塩水 100 g をとって、それを ③ ( 容器 B ) に入れてよくかき混ぜたときの容器 B の食塩水
混ぜたあとの食塩の量 7 + 15 = 22 [g]、食塩水の量は 100 + 100 = 200 [g]、濃度は 22 ÷ 200 × 100 = 11 [%]
④ の食塩水 100 g に含まれる食塩の量は、100 × 0.11 = 11 [g]
⑤:④ ( 容器 B ) から食塩水 100 g をとって、それを ② ( 容器 A ) に入れてよくかき混ぜたときの容器 A の食塩水
食塩の量は 45 + 11 = 56 [g]、食塩水の量は 300 + 100 = 400 [g]
56 ÷ 400 × 100 = 14 [%]
(3)6 % の食塩水があります。この食塩水に操作ア、操作イを何回か行います。
操作ア:食塩水を全体の重さの \(\dfrac{3}{5}\) だけ残して、それ以外の食塩水は捨てる。その後捨てた食塩水と同じ重さだけ 16 % の食塩水を加える。
操作イ:食塩水を全体の重さの \(\dfrac{1}{2}\) だけ残して、それ以外の食塩水は捨てる。その後捨てた食塩水と同じ重さだけ水を加える。
① 操作アを 1 回行うと何 % の食塩水ができますか。
- 答え(3)- ①
- 10 %
- 解き方(3)- ①
- 操作アを行う前の 6 % の食塩水の全体の重さを \(\boxed{1}\) とする。
残す食塩水の重さは \(\boxed{\dfrac{3}{5}}\) 、捨てる食塩水( = 加える 16 % の食塩水 ) の重さは \(\boxed{\dfrac{2}{5}}\) となる。
操作アを行った後の食塩水の重さは \(\boxed{1}\) 、含まれる食塩の重さは \(\dfrac{6}{100}\) × \(\boxed{\dfrac{3}{5}}\) + \(\dfrac{16}{100}\) × \(\boxed{\dfrac{2}{5}}\) = \(\boxed{\dfrac{1}{10}}\)
よってその濃度は、
\(\boxed{\dfrac{1}{10}}\) ÷ \(\boxed{1}\) × 100 = 10 [%]
② 操作アを 1 回行ってから、操作イを続けて 3 回行うと何 % の食塩水ができますか。
- 答え(3)- ②
- 1.25 %
- 解き方(3)- ②
- ① より、操作アを 1 回行った後の食塩水の濃度は 10 %、食塩水の重さは \(\boxed{1}\) 、含まれる食塩の重さは \(\boxed{\dfrac{1}{10}}\) である。
操作イを 1 回行うごとに、含まれる食塩の重さは \(\dfrac{1}{2}\) になるが、食塩水全体の重さは \(\boxed{1}\) のままである。
よって、操作イを 3 回行った後の食塩水の濃度は、
( \(\boxed{\dfrac{1}{10}}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\) ) ÷ \(\boxed{1}\) × 100 = 1.25 [%]





