算数【応用】集合・ベン図
問1
あるクラスで算数と国語のテストを行いました。算数の合格者数と、国語の合格者数の比は 6:5 でした。算数だけ合格した生徒は 4 人、算数も国語も合格した生徒はクラスの \(\dfrac{1}{4}\) にあたる 8 人でした。算数も国語も不合格だった生徒は何人ですか。
- 答え
- 18 人
- 解き方
- クラス全体の人数は 8 × 4 = 32 [人]
算数の合格者数を⑥、国語の合格者数を⑤とする。
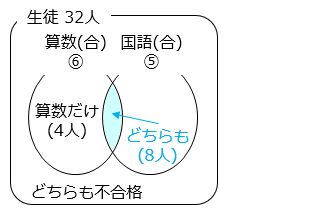
算数の合格者は、
⑥ = 4 + 8 = 12 [人]
よって、① = 2 より国語の合格者は、
⑤ = 5 × 2 = 10 [人]
したがって、どちらも不合格だった生徒は、
32 – ( 4 + 10 ) = 18 [人]
問2
ある文房具店ではノートをえんぴつの 1.5 倍の値段で売っています。ある日、180 人の人が来て、えんぴつ 1 本のみか、ノート 1 冊のみか、またはえんぴつ 1 本とノート 1 冊を買いました。えんぴつを買った人は全体の \(\dfrac{2}{3}\)、ノートを買った人は全体の \(\dfrac{3}{5}\) でした。また、えんぴつ 1 本とノート 1 冊の両方を買った人が支払った金額の合計は 7200 円でした。
(1)えんぴつだけ買った人は何人ですか。
- 答え(1)
- 72 人
- 解き方(1)
- えんぴつを買った人は 180 × \(\dfrac{2}{3}\) = 120 [人]
ノートを買った人は 180 × \(\dfrac{3}{5}\) = 108 [人]
えんぴつとノートの両方を買った人は 120 + 108 – 180 = 48 [人]
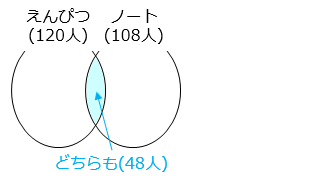
えんぴつだけ買った人は、
120 – 48 = 72 [人]
(2)ノート 1 冊の値段はいくらですか。
- 答え(2)
- 90 円
- 解き方(2)
- えんぴつ 1 本の値段を □ [円]とすると、ノート 1 冊の値段は 1.5 × □ [円] と表すことができ、合計で □ + 1.5 × □ = 2.5 × □ [円] となる。
よって、次の式が成り立つ。
2.5 × □ = 7200 ÷ 48
2.5 × □ = 150
□ = 150 ÷ 2.5 = 60 [円]
□ = 60 [円]
ノート 1 冊の値段は、
1.5 × □ = 1.5 × 60 = 90 [円]
問3
あるクラスで動物園に行ったことがある人は 16 人、水族館に行ったことがある人は 19 人います。両方に行ったことがある人は、動物園に行ったことがある人の \(\dfrac{3}{8}\) で、クラス全体の \(\dfrac{1}{6}\) です。動物園と水族館のどちらにも行ったことがない人は何人ですか。
- 答え
- 7 人
- 解き方
- 両方に行ったことがある人は 16 × \(\dfrac{3}{8}\) = 6 [人]
クラス全体の人数を □ 人とすると、次の式が成り立つ。
□ × \(\dfrac{1}{6}\) = 6
□ = 6 × 6 = 36 [人]
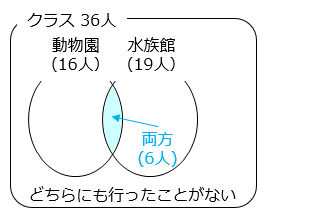
どちらにも行ったことがない人は、
36 – ( 16 + 19 – 6 ) = 7 [人]
問4
50 人の生徒が旅行先で、1 個 200 円のみやげ A と 1 個 150 円のみやげ B を買うことになりました。A、B 両方とも買った生徒が 4 人、両方とも買わなかった生徒が 16 人いて、全員のみやげ代金の合計は 6800 円でした。また、同じ種類のみやげを 2 個以上買った生徒はいませんでした。みやげ B だけを買った生徒は何人ですか。
- 答え
- 12 人
- 解き方
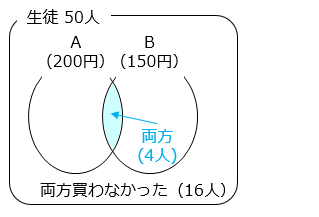
A だけを買った生徒と B だけを買った生徒の合計は、
50 – 16 – 4 = 30 [人]
これらの生徒が支払ったみやげ代金の合計は、
6800 – ( 200 + 150 ) × 4
= 6800 – 1400 = 5400 [円]
【つるかめ算を利用する】
これらの 30 人の生徒が全員 A を買ったとすると、その代金は 200 × 30 = 6000 [円] であるが、実際の代金は 5400 円。
よって B を買った生徒は、
( 6000 – 5400 ) ÷ ( 200 – 150 )
= 600 ÷ 50 = 12 [人]
【消去算を利用する】
A だけを買った生徒を a 人、B だけを買った生徒を b 人とすると、以下の式が成り立つ。
a + b = 30 ・・・ ①
200 × a + 150 × b = 5400 ・・・ ②
① × 200 – ② より、
( 200 – 150 ) × b = 6000 – 5400
50 × b = 600
b = 12 [人]
問5
300 人の生徒に通学に関するアンケートをとったところ、電車を使っている生徒は 250 人、バスを使っている生徒は 75 人いました。このとき、電車もバスも両方使っている生徒は何人以上何人以下と考えられますか。
- 答え
- 25 人以上 75 人以下
- 解き方
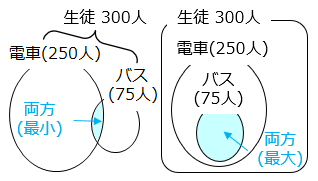
両方使っている生徒の人数が最小のときは、電車とバスを使っている生徒の合計が 300 人になるときより、
250 + 75 – 300 = 25 [人]
両方使っている生徒の人数が最大のときは、バスを使っている生徒が全員電車も使っているときより、75 人。
よって、25 人以上 75 人以下と考えられる。
問6
40 人のクラスでボール投げと反復横とびをしました。ボール投げで 25 m より遠くに投げた人が 24 人、反復横とびが 40 回以上の人が 12 人、ボール投げが 25 m 以下で反復横とびが 39 回以下の人は 7 人でした。
(1)ボール投げで 25 m より遠くに投げた人で、反復横とびが 40 回以上の人は何人ですか。
- 答え(1)
- 3 人
- 解き方(1)
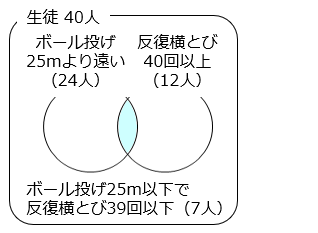
部分の人数。
ボール投げで 25 m より遠くに投げた人と反復横とびが 40 回以上の人の合計は 40 – 7 = 33 [人] より、
求める人数は、
( 24 + 12 ) – 33 = 3 [人]
(2)ボール投げが 25 m 以下の人で、反復横とびが 40 回以上の人は何人ですか。
- 答え(2)
- 9 人
- 解き方(2)
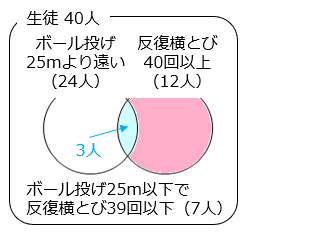
部分の人数。
12 – 3 = 9 [人]
問7
36 人の生徒にアンケートをしました。犬を飼っている生徒は 8 人で、猫を飼っている生徒は 19 人でした。この結果から、犬も猫も飼っていない生徒は、何人以上何人以下と考えることができますか。
- 答え
- 9 人以上 17 人以下
- 解き方
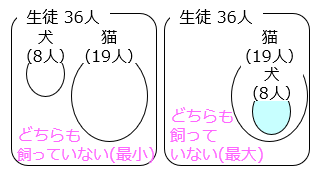
どちらも飼っていない生徒が最小になるとき、犬または猫を飼っている生徒の合計が最も大きいとき。
犬または猫を飼っている生徒の合計が最も大きいときは 8 + 19 = 27 [人] のときより、どちらも飼っていない生徒は 36 – 27 = 9 [人]
どちらも飼っていない生徒が最大になるとき、犬または猫を飼っている生徒の合計が最も小さいとき。
犬または猫を飼っている生徒の合計が最も小さいときは 19 人のときより、どちらも飼っていない生徒は 36 – 19 = 17 [人]
よって、9 人以上 17 人以下と考えることができる。
問8
ある学年の生徒 128 人に、動物園、水族館、植物園の中から、行きたい場所を選んでもらいました。1 人いくつ選んでもかまいませんが、少なくとも 1 つは選ぶことにしたところ、次のような結果になりました。
動物園を選んだ人・・・・・・・ 95 人
水族館を選んだ人・・・・・・・ 72 人
植物園を選んだ人・・・・・・・ 53 人
動物園と水族館を選んだ人・・・ 45 人
水族館と植物園を選んだ人・・・ 26 人
植物園と動物園を選んだ人・・・ 35 人
(1)動物園と水族館と植物園をすべて選んだ生徒は何人ですか。
- 答え(1)
- 14 人
- 解き方(1)
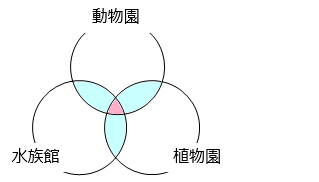
動物園、水族館、植物園を選んだ生徒の合計は、
95 + 72 + 53 = 220 [人] ・・・ ①
このとき、白色部分(1 つを選んだ人数)は 1 回、 部分(2 つを選んだ人数)は 2 回、 部分(すべてを選んだ人数)は 3 回足されている。
動物園と水族館、水族館と植物園、植物園と水族館を選んだ生徒の合計は、
45 + 26 + 35 = 106 [人] ・・・ ②
このとき、 部分は 1 回、 部分は 3 回足されている。
① – ② より、白色部分と 部分の人数が求められる。
① – ② = 220 – 106 = 114 [人]
よってすべて選んだ生徒は、
128 – 114 = 14 [人]・・・ ③
(2)動物園、水族館、植物園のいずれか 1 つだけを選んだ生徒は何人ですか。
- 答え(2)
- 50 人
- 解き方(2)
- 求める人数は、
① – ② × 2 + ③ × 3 より、
220 – 106 × 2 + 14 × 3
= 220 – 212 + 42 = 50 [人]
問9
あるクラスで算数のテストをしました。A の問題は 4 点、B の問題は 6 点で合計 10 点満点です。A ができた人は 21 人、B ができた人は 28 人、A と B の両方ができた人は 13 人、両方できなかった人は 4 人でした。
(1)クラスの人数は何人ですか。
- 答え(1)
- 40 人
- 解き方(1)
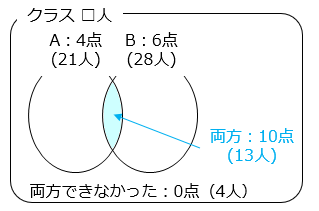
( 21 + 28 – 13 ) + 4 = 40 [人]
(2)A だけができた人はクラス全体の何 % ですか。
- 答え(2)
- 20 %
- 解き方(2)
- A だけができた人は 21 – 13 = 8 [人] より、
8 ÷ 40 × 100 = 20 [%]
(3)このテストの平均点は何点ですか。
- 答え(3)
- 6.3 点
- 解き方(3)
- A だけができた人:4 点、 8 人
B だけができた人:6 点、 28 – 13 = 15 [人]
両方できた人:10 点、 13 人
両方できなかった人:0 点、 4 人
平均点は、
( 4 × 8 + 6 × 15 + 10 × 13 + 0 × 4 ) ÷ 40
= 252 ÷ 40
= 6.3 [点]
問10
あるクラスで、算数、国語、理科のうちから好きな教科を選ぶことになりました。クラス 40 人全員が、必ず 3 つのうちのどれか 1 つ以上を選ばなければなりません。
下の ① ~ ⑥ を読んで、以下の問いに答えなさい。
① 理科だけを選んだ人は 1 人でした。
② 算数を選んだ人は 24 人でした。
③ 国語を選んだ人は 20 人でした。
④ 2 つの教科だけを選んだ人は 10 人でした。
⑤ 1 つの教科だけを選んだ人は 27 人でした。
⑥ 算数と理科の両方を選んだ人は 11 人でした。
(1)3 つの教科すべてを選んだ人は何人ですか。
- 答え(1)
- 3 人
- 解き方(1)
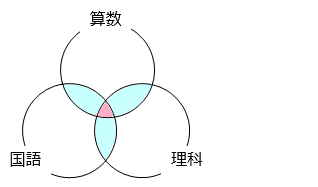
④ より、2 つの教科だけを選んだ人( 部分)は 10 人
⑤ より、1 つの教科だけを選んだ人(白色部分)は 27 人
よって、すべてを選んだ人( 部分)は、
40 – ( 10 + 27 ) = 3 [人]
(2)国語だけを選んだ人は何人ですか。
- 答え(2)
- 15 人
- 解き方(2)
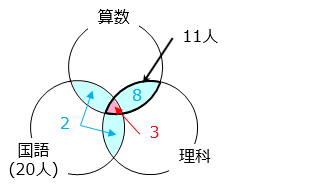
⑥ より、太線で囲まれた部分は 11 人なので、算数と理科だけを選んだ人は 11 – 3 = 8 [人]
④ より、 部分の合計は 10 人なので、算数と国語だけ選んだ人と国語と理科だけ選んだ人の合計は 10 – 8 = 2 [人]
③ より国語を選んだ人は 20 人なので、国語だけを選んだ人は、
20 – ( 2 + 3 ) = 15 [人]
(3)算数だけを選んだ人は何人ですか。
- 答え(3)
- 11 人
- 解き方(3)
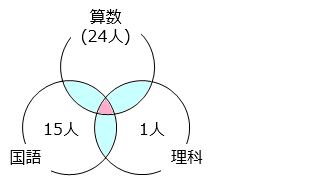
① より、理科だけを選んだ人は 1 人
(2)より、国語だけを選んだ人は 15 人
⑤ より、1 つの教科だけを選んだ人は 27 人
よって、算数だけを選んだ人は、
27 – ( 1 + 15 ) = 11 [人]













