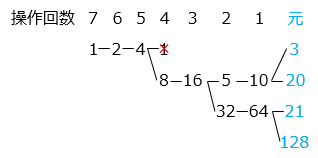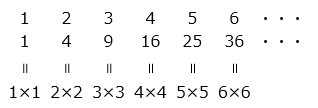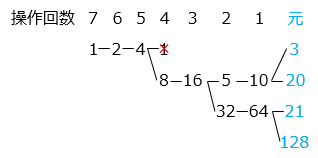算数【応用】周期算
問1
ある規則にしたがって、分数を並べました。
\(\dfrac{8}{2}\), \(\dfrac{7}{4}\), \(\dfrac{6}{6}\), \(\dfrac{5}{2}\), \(\dfrac{8}{4}\), \(\dfrac{7}{6}\), \(\dfrac{6}{2}\), \(\dfrac{5}{4}\), \(\dfrac{8}{6}\), \(\dfrac{7}{2}\), \(\dfrac{6}{4}\), \(\dfrac{5}{6}\), \(\dfrac{8}{2}\), \(\dfrac{7}{4}\), \(\dfrac{6}{6}\), …
(1)10回目に出てくる \(\dfrac{7}{6}\) は、左から数えて何番目ですか。
- 答え(1)
- 114番目
- 解き方(1)
- 分子の並びは「8, 7, 6, 5」の4個1組の繰り返し、分母は「2, 4, 6」の3個1組の繰り返しになっている。1回目に出てくる\(\dfrac{7}{6}\)は6番目で、以降は4と3の最小公倍数12番ごとにでてくるので、
6 + 12 × (10 – 1) = 114(番目) (2)100番目までに出てくる分数の中で、約分できない分数をすべて加えるといくつになりますか。
- 答え(2)
- 92\(\dfrac{1}{4}\)
- 解き方(2)
- 分数の並びは「\(\dfrac{8}{2}\), \(\dfrac{7}{4}\), \(\dfrac{6}{6}\), \(\dfrac{5}{2}\), \(\dfrac{8}{4}\), \(\dfrac{7}{6}\), \(\dfrac{6}{2}\), \(\dfrac{5}{4}\), \(\dfrac{8}{6}\), \(\dfrac{7}{2}\), \(\dfrac{6}{4}\), \(\dfrac{5}{6}\)」の12個1組の繰り返しになっている。その中で約分できない分数は、\(\dfrac{7}{4}\), \(\dfrac{5}{2}\), \(\dfrac{7}{6}\), \(\dfrac{5}{4}\), \(\dfrac{7}{2}\), \(\dfrac{5}{6}\)で、その和は11。100 ÷ 12 = 8 あまり 4 より、
11 × 8 + \(\dfrac{7}{4}\) + \(\dfrac{5}{2}\) = 92\(\dfrac{1}{4}\)
問2
表のように、上段には14個のアルファベット「A、B、C、D、E、F、G、H、I、J、K、L、M、N」がこの順で繰り返し並んでいます。下段は10個のひらがな「あ、い、う、え、お、か、き、く、け、こ」がこの順で繰り返し並んでいます。
| 上段 | A | B | C | D | E | F | G | H | I | J | K | L | M | N | A | B | … |
|
| 下段 | あ | い | う | え | お | か | き | く | け | こ | あ | い | う | え | お | か | … |
(1)2回目に「A」と「あ」が上下に並ぶのは、左から何番目ですか。
- 答え(1)
- 71番目
- 解き方(1)
- 上段の並びは14個1組の繰り返し、下段の並びは10個1組の繰り返しになっている。よって、同じ組み合わせは14と10の最小公倍数である70番ごとに出てくる。よって、
1 + 70 = 71(番目) (2)「I」と「う」がはじめて上下に並ぶのは、左から何番目ですか。
- 答え(2)
- 23番目
- 解き方(2)
- 1回目の「I」が出てくるのは9番目で、以降14番ごとに出てくる ⇒ 14で割ると9余る数が「I」の出てくる番数
1回目の「う」が出てくるのは3番目で、以降10番ごとに出てくる ⇒ 10で割ると3余る数が「う」の出てくる番数
求める番数は、14で割ると9余り、10で割ると3余る最小の数
14で割ると9余る数は、9, 23, ・・・
10で割ると3余る数は、3, 13, 23, ・・・
よって、23番目
問3
\(\boxed{1}\) \(\boxed{2}\) ③ \(\boxed{4}\) ⑤ ⑥ \(\boxed{7}\) \(\boxed{8}\) ⑨ \(\boxed{10}\) ① ② \(\boxed{3}\) \(\boxed{4}\) ⑤ \(\boxed{6}\) ⑦ ⑧ \(\boxed{9}\) \(\boxed{10}\) ① …
数字の書かれた□と○が規則にしたがって並んでいます。数字の1が書かれた□を「 四角の1」、数字の1が書かれた○を「丸の1」とします。
下記の \(\boxed{ }\)に当てはまる文字または数字を答えなさい。
(1)左側から50番目までに丸は \(\boxed{ア}\) 個並んでいます。また、丸に書かれた数字の和は \(\boxed{イ}\) です。
- 答え(1)
- ア:24 イ:126
- 解き方(1)
- 数字と図形の別の並びと考えると、
| □ | □ | ○ | □ | ○ | ○ | □ | □ | ○ | □ | ○ | ○ | □ | … |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | … |
図形の並びは「□, □, ○, □, ○, ○」の6個1組の繰り返しで、そのうち○は3個。50 ÷ 6 = 8 あまり 2 より、○の個数は、
3 × 8 = 24(個)
数字の並びは「1, 2, 3, …, 10」の10個1組の繰り返しとなっている。図形と数字の組み合わせはそれぞれの1組の個数の最小公倍数である30個1組の繰り返しになっている。
| □ | □ | ○ | □ | ○ | ○ |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 |
| 合計:25 | 合計:30 | 合計:25 | 合計:30 | 合計:25 | 合計:30 |
この30個中の○の数字の和は、25 + 25 + 30 = 80
50 ÷ 30 = 1 あまり 20
80 × 1 + (80 – 10 – 9 – 7 – 4 – 3 – 1) = 126 (2)左から150番目までに「四角の2」は \(\boxed{ }\) 個並んでいます。
- 答え(2)
- 10
- 解き方(2)
| □ | □ | ○ | □ | ○ | ○ |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 |
図形と数字の組み合わせはそれぞれの1組の個数の最小公倍数である30個1組の繰り返しになっている。そのうち、\(\boxed{2}\) は2個。
150 ÷ 30 = 5 あまり 0 より、\(\boxed{2}\) の個数は、2 × 5 = 10(個)(3)17個目の「丸の7」は、左から \(\boxed{ }\) 番目です。
- 答え(3)
- 257
- 解き方(3)
| □ | □ | ○ | □ | ○ | ○ |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 1 | 2 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 | 10 |
図形と数字の組み合わせはそれぞれの1組の個数の最小公倍数である30個1組の繰り返しになっている。そのうち、⑦は2個。
17 ÷ 2 = 8 あまり 1 より、30 × 8 + 17 = 257(番目)
問4
1番目の数は1とし、偶数番目の数は1つ前の数に2を足し、奇数番目の数は1つ前の数に1を足します。この規則にしたがって、数を並べます。
1, 3, 4, 6, 7, 9, …
(1)100番目の数はいくつですか。
- 答え(1)
- 150
- 解き方(1)
- 1, 4, 7と3, 6, 9の数字の組み合わせになっている。100番目は偶数なので、3, 6, 9の数字の一部である。
したがって、3, 6, 9の半分の50番目の数字が100番目の数字にあたる。
n番目の数字 × 3 がその数になるので、3 × 50 = 150
【別解】
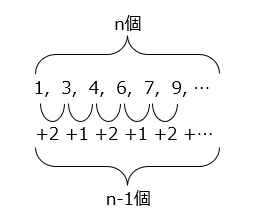
図のように、この数の並びは、1に2と1を順に繰り返し足した数の並びである。n個の数が並んでいるとき、足した数の数は(n-1)個である。
100番目の数は1に2と1を順に99個足した数となる。99 ÷ 2 = 49 あまり 1 より、100番目の数は、1 + (2 + 1) × 49 + 2 = 150 (2)1番目から2121番目までに偶数は何個ありますか。
- 答え(2)
- 1060個
- 解き方(2)
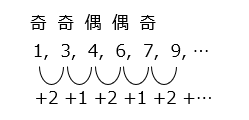
図のように、この数の並びは、「奇数、奇数、偶数、偶数」の4個1組の繰り返しで、そのうち偶数は2個ある。2121 ÷ 4 = 530 あまり 1 より、偶数は、530 × 2 = 1060(個)
問5
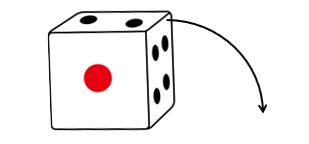
向かい合う面の数の和が7になるサイコロがあります。このサイコロを図のように置き、すべらせることなく矢印の方向に563回ころがしたとき、真下を向く面の和はいくつですか。例えば2回ころがしたときの真下を向く面の和は 4 + 2 = 6 となります。
- 答え
- 1969
- 解き方
- 真下を向く面の数字は「4, 2, 3, 5」の4個1組の繰り返しで、その和は14。563 ÷ 4 = 140 あまり 3 より、567回ころがしたときの真下を向く面の和は、14 × 140 + 4 + 2 + 3 = 1969
問6
規則にしたがって、白玉と黒玉を1から順に並んだ数字の下に並べていきます。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| ○ | ○ | ○ | ● | ● | ● | ○ | ○ | ○ | ● | … |
| ○ | ○ | ● | ● | ○ | ○ | ● | ● | ○ | ○ | … |
| ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | … |
(1)すべて白玉が並ぶ数字は、250番目までに何個ありますか。
- 答え(1)
- 42個
- 解き方(1)
- 1段目は「○○○●●●」の6個1組、2段目は「○○●●」の4個1組、3段目は「○●」の2個1組の繰り返しになっていて、すべての段はそれぞれの段の個数の最小公倍数である12番ごとの繰り返しになっている。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| ○ | ○ | ○ | ● | ● | ● | ○ | ○ | ○ | ● | ● | ● |
| ○ | ○ | ● | ● | ○ | ○ | ● | ● | ○ | ○ | ● | ● |
| ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● |
そのうちすべて白玉が並んでいる数字は2回。250 ÷ 12 = 20 あまり 10 より、白玉が並ぶ数字は、2 × 20 + 2 = 42(個) (2)1から100までに黒玉は何個ありますか。
- 答え(2)
- 149個
- 解き方(2)
- 1段目は「○○○●●●」の6個1組、2段目は「○○●●」の4個1組、3段目は「○●」の2個1組の繰り返しになっていて、すべての段はそれぞれの段の個数の最小公倍数である12番ごとの繰り返しになっている。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| ○ | ○ | ○ | ● | ● | ● | ○ | ○ | ○ | ● | ● | ● |
| ○ | ○ | ● | ● | ○ | ○ | ● | ● | ○ | ○ | ● | ● |
| ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● |
そのうち黒玉は18個。100 ÷ 12 = 8 あまり 4 より、黒玉は、18 × 8 + 1 + 1 + 3 = 149(個) (3)黒玉の合計が281個になるときの数字はいくつですか。
- 答え(3)
- 188
- 解き方(3)
- 1段目は「○○○●●●」の6個1組、2段目は「○○●●」の4個1組、3段目は「○●」の2個1組の繰り返しになっていて、すべての段はそれぞれの段の個数の最小公倍数である12番ごとの繰り返しになっている。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| ○ | ○ | ○ | ● | ● | ● | ○ | ○ | ○ | ● | ● | ● |
| ○ | ○ | ● | ● | ○ | ○ | ● | ● | ○ | ○ | ● | ● |
| ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● | ○ | ● |
そのうち黒玉は18個。281 ÷ 18 = 15 あまり 11 より、黒玉の合計が281個になるときの数字は、12 × 15 + 8 = 188
問7
はじめの数は1とし、その後は前の数に1, 0, 3, 5, 1, 0, 3, 5, …の順に繰り返し数を足します。この規則にしたがって、数を並べます。
1, 2, 2, 5, 10, 11, 11, 14, 19, 20 …
(1)28番目の数はいくつですか。
- 答え(1)
- 59
- 解き方(1)
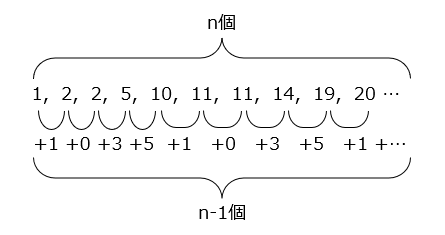
n個の数が並んでいるとき、足した数の数は(n-1)個である。
28番目の数は1に「1, 0, 3, 5」の4個の数を繰り返し27個足した数となる。27 ÷ 4 = 6 あまり 3 より、28番目の数は、1 + (1 + 0 + 3 + 5) × 6 + 1 + 0 + 3 = 59(2)はじめて500より大きくなる数は、何番目の数ですか。
- 答え(2)
- 225番目
- 解き方(2)
- 4個の数「1, 0, 3, 5」の和は9。
1 + 9 × 55 = 496
496 + 1 = 497
496 + 1 + 0 = 497
496 + 1 + 0 + 3 = 500
496 + 1 + 0 + 3 + 5 = 505
496は 55 × 4 + 1 = 221(番目)なので、505は 221 + 4 = 225(番目)
問8
次のように、ある規則に従って並んでいる数の列があります。
1, 4, 9, 16, 25, 36, ・・・
この数列の各数を 6 で割った余りを左から順番に並べて新しい数の列を作ります。この新しい数列について、次の問いに答えなさい。
(1)はじめから数えて 50 番目の数はいくつですか。
- 答え(1)
- 4
- 解き方(1)
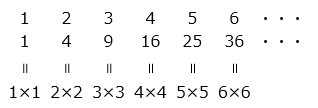
元の数列は各項の番号の 2 乗の数になっている。よって、元の数列の 50 番目の数は 50 × 50 = 2500 である。よって、新しい数列の数は 6 で割った余りより、
2500 ÷ 6 = 416 余り 4
(2)4 が 10 回目に現れるのは、はじめから数えて何番目ですか。
- 答え(2)
- 28 番目
- 解き方(2)

新しい数列は ( 1, 4, 3, 4, 1, 0 ) の 6 個の数を群とした周期数列になっている。
各群には 4 が 2 個ずつあることから、4 が 10 回目に現れるのは 5 群の 4 番目と考えられる。よって、
4 × 6 + 4 = 28 [番目]
(3)はじめの数から 2025 番目の数までの和はいくつですか。
- 答え(3)
- 4389
- 解き方(3)
- 新しい数列は ( 1, 4, 3, 4, 1, 0 ) の 6 個の数を群とした周期数列になっている。
2025 ÷ 6 = 337 余り 3 より、2025 番目の数までの和は、
( 1 + 4 + 3 + 4 + 1 + 0 ) × 337 + ( 1 + 4 + 3)
= 13 × 337 + 8 = 4389
問9
ある整数から、次の<操作>をくり返し行い、<操作>でできた数を順にならべて列をつくります。
<操作>その整数が偶数なら 2 で割り、奇数なら 3 倍して 1 を足す
例えば、11 から<操作>をくり返し行うと、11 は奇数なので、11 を 3 倍して 1 を足して、1 回目の<操作>でできた数は 34 となります。つぎに、34 は偶数なので、 34 を 2 で割って、2 回目の<操作>でできた数は 17 となります。このようにしてできた数を順にならべると、
34, 17, 52, 26, ・・・
という数の列になります。このとき、26 ができるまでに<操作>は 4 回行っています。
(1)12 から<操作>をくり返し行います。はじめて 1 ができるのは<操作>を何回行ったときですか。
- 答え(1)
- 9 回
- 解き方(1)
- 12 → 6, 3, 10, 5, 16, 8, 4, 2, 1
はじめの「1」は 9 番目の数より、<操作>を行った回数は 9 回
(2)10 から<操作>をくり返し行います。2325 回目の<操作>でできる数はいくつですか。
- 答え(2)
- 1
- 解き方(2)
- 10 → 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, ・・・
4 番目の数 ( 4 回目の<操作> でできる数 ) 以降は、( 4, 2, 1 ) の 3 つの数のくり返しになる。
( 2325 – 3 ) ÷ 3 = 774 余り 0
より、2325 番目の数は 1
(3)7 回目の<操作>を行ったときにはじめて 1 ができるような数をすべて求め、小さい順に答えなさい。
- 答え(3)
- 3, 20, 21, 128
- 解き方(3)
- 1 から 1 を引くと 0 となり 3 で割ることができないので、前の数は偶数で 2
2 から 1 を引くと 1 となり 3 の倍数ではないので、前の数は偶数で 4
4 から 1 を引くと 3 となり 3 で割ると 1 より、前の数が奇数の場合 1、偶数の場合 8
このように、<操作>を さかのぼっていくと以下のようになる。