算数【応用】旅人算
問1
分速 92 m で出発した兄を、弟が同じ場所から 4 分後に自転車で追いかけたら、その 8 分後に追いつきました。このとき、弟の自転車の速さは分速何 m ですか。
- 答え
- 分速 138 m
- 解き方
- 兄が出発してから弟が追いつくまでの総移動時間は、4 + 8 = 12 [分]
兄の移動距離は、92 × 12 = 1104 [m]
弟が移動にかかった時間は 8分なので
1104 ÷ 8 = 138 [m/分]
【別解】
兄が 4 分の間に進んだ距離は 92 × 4 = 368 [m]より、弟の自転車の速さを分速 □ m とすると、次の式が成り立つ。
8 × ( □ – 92 ) = 368
□ – 92 = 368 ÷ 8 = 46
□ = 46 + 92 = 138 [m/分]
問2
周りの長さが 2400 m ある池の周りを、同じ場所から兄弟が同時に出発して同じ方向に進むと 60 分で兄は弟に追いつきます。反対方向に進むと 12 分で出会います。兄の速さは分速何 m ですか。
- 答え
- 分速 120 m
- 解き方
- 兄の速さを分速 A m、弟の速さを分速 B m とすると、以下の式が成り立つ。
60 × ( A – B ) = 2400 ⇒ A – B = 40・・・ ①
12 × ( A + B ) = 2400 ⇒ A + B = 200・・・ ②
② + ① より、
2 × A = 240
A = 120 [m/分]
問3
家から姉が、学校から妹が同時に向かい合って出発します。姉は分速 70 m、妹は分速 40 m で歩きます。出会うまでに妹は途中で 2 分休憩しました。また、出会うまでに姉は妹よりも 440 m 多く歩きました。家から学校までの距離は何 m ですか。
- 答え
- 1240 m
- 解き方
- 出会うまでに妹は途中で 2 分休憩しました。⇒ 妹は姉より 2 分遅れて出発したと考える。
2 分の間に姉が進んだ距離は 70 × 2 = 140 [m]より、姉妹が出会うまでに歩いた距離の差は 440 – 140 = 300 [m] となる。よって、出会うまでにかかった時間を □ 分とすると、次の式が成り立つ。
( 70 – 40 ) × ( □ – 2 ) = 300
30 × ( □ – 2 ) = 300
30 × □ = 360
□ = 12 [分]
家から学校までの距離は、
70 × 12 + 40 × ( 12 – 2 )
= 840 + 400 = 1240 [m]
【別法】式を作る
出会うまでにかかった時間を □ 分とする。

70 × □ – 440 = 40 × ( □ – 2 ) = 40 × □ – 80
30 × □ = 360
□ = 12 [分]
家から学校までの距離は、
70 × 12 + 40 × ( 12 – 2 )
= 840 + 400 = 1240 [m]
問4
ある池の周りを A さんと B さんが走ります。B さんは分速 100 m の速さで走ります。2 人が同じ場所から同時に出発し、同じ方向に走ると A さんは B さんに 26 分後に追いつき、反対方向に走ると 6 分後に初めて出会います。2 人がそれぞれ一定の速さで走るとき、A さんの走る速さは分速何 m ですか。
- 答え
- 分速 160 m
- 解き方
- A さんの走る速さを分速 □ m とする ( □ > 100 ) と、次の式が成り立つ。
26 × ( □ – 100 ) = 6 × ( □ + 100 )
26 × □ – 2600 = 6 × □ + 600
20 × □ = 3200
□ = 160 [m/分]
問5
あるジョギングコースを 1 周するのに兄は 8 分、弟は 12 分かかります。兄と弟が同時にスタートし地点から同じ方向に走り出しました。兄が弟を初めて追いこすのは 2 人がスタートしてから何分後ですか。
- 答え
- 24 分後
- 解き方
- 同じ距離を移動するためにかかる時間は、速さと反比例する。よって、兄と弟の走る速さを比で表すと、12:8 = 3:2 となる。兄の速さを分速③とすると、弟の速さは分速②、ジョギングコースの距離は ③ × 8 = ㉔ と表すことができる。
兄が弟を初めて追いこすのにかかる時間は、
㉔ ÷ ( ③ – ② ) = 24 [分後]
問6
姉と妹は同じ道を歩いて同じ学校に通っています。妹は午前 7 時 45 分に家を出て毎分 64 m の速さで歩き、姉は午前 7 時 48 分に家を出て毎分 80 m の速さで歩きます。姉が妹に追いついたのが、学校の677 m 手前だったとするとき、家から学校までの道のりを求めなさい。
- 答え
- 1637 m
- 解き方
- 姉は妹より 3 分遅れて家を出る。姉が家を出るとき、妹は家から 64 × 3 = 192 [m] 進んでいる。よって、姉が妹に追いつくのにかかる時間は、
192 ÷ ( 80 – 64 ) = 12 [分]
したがって、姉が妹に追いついたのは、家から 80 × 12 = 960 [m] の地点となる。
よって、家から学校までの道のりは 960 + 677 = 1637 [m]
問7
兄と弟が 1200 m 競走をしました。弟がスタートしてから 1 分後に兄がスタートしたところ、途中で兄が追いこし、兄が先にゴールしました。兄がゴールしたとき、弟はゴールの何 m 手前を走っていましたか。ただし、兄は毎分 240 m、弟は毎分 180 m の速さで走り続けたものとします。
- 答え
- 120 m
- 解き方
- 兄がゴールするのにかかる時間は、1200 ÷ 240 = 5 [分]
弟が走った距離は、180 × ( 5 + 1 ) = 1080 [m]
ゴールまでの距離は1200 mなので、弟がゴールの手前にいる距離は
1200 – 1080 = 120 [m]
【別解】
兄が弟を追いこしたのは、兄がスタートしてから 180 ÷ ( 240 – 180 ) = 3 [分後] である。よって、兄が弟を追いこしたのは、ゴールから 1200 – 3 × 240 = 480 [m] の地点となる。
兄がゴールしたのは、弟を追いこしてから 480 ÷ 240 = 2 [分後]
このとき弟がいたのはゴールから、480 – 180 × 2 = 120 [m] 手前の地点。
問8
グラフは A 駅と B 駅の間を、時速 30 km の普通列車と時速 60 km の急行列車が運行する時間と位置の関係を表したものです。急行列車は普通列車が A 駅を出発してから 7 分後に A 駅を出発します。普通列車は途中の C 駅で停車している 3 分の間に急行列車に追い抜かれます。急行列車は B 駅で 5 分停車してから A 駅に向かって発車します。ただし、列車の長さは考えないものとします。
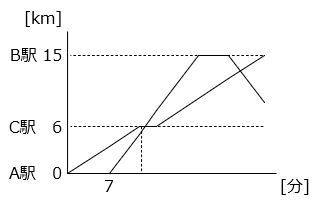
(1)急行列車が C 駅を通過するのは普通列車が C 駅に到着してから何分後ですか。
- 答え(1)
- 1 分後
- 解き方(1)
- 普通列車 時速 30 km = 分速 0.5 km
急行列車 時速 60 km = 分速 1 km
普通列車が C 駅に到着するのは発車してから 6 ÷ 0.5 = 12 [分後]
急行列車が C 駅を通過するのは発車してから 6 ÷ 1 = 6 [分後] より、普通列車が発車してから 7 + 6 = 13 [分後]
よって、急行列車が C 駅を通過するのは、普通列車が C 駅に到着してから 1 分後。
(2)B 駅で折り返してきた急行列車が普通列車とすれ違うのは A 駅から何 km の地点ですか。
- 答え(2)
- 13 km
- 解き方(2)
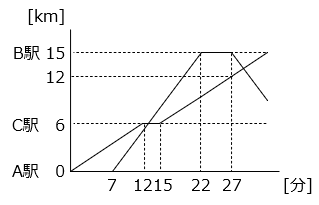
急行列車が B 駅に到着するのは、発車してから 15 ÷ 1 = 15 [分後] より、普通列車が A 駅を発車してから 7 + 15 = 22 [分後]
急行列車が B 駅を発車するのは 22 + 5 = 27 [分後] となる。
このとき、普通列車は C 駅を発車してから 27 – 15 = 12 [分後] より、C 駅から 0.5 × 12 = 6 [km] の地点、すなわち A 駅から 6 + 6 = 12 [km]、B 駅から 15 – 12 = 3 [km] の地点にいる。
2 つの列車がすれ違うのは、普通列車がこの地点から 3 ÷ ( 1 + 0.5 ) = 2 [分後] に到達した地点となる。したがって、A 駅から、
12 + 0.5 × 2 = 13 [km] の地点
問9
A さんと B さんは、片道 3600 m の道を折り返す往復 7200 m のマラソンをしました。A さんは、行きも帰りも一定の速さで走りました。一方、B さんは A さんと同時に出発し、行きは一定の速さで走りましたが、A さんよりも遅れていたため、帰りは行きよりも速い一定の速さで走り、A さんより 6 分遅れてゴールしました。グラフは、 A さんと B さんが出発してからの時間と A さんと B さんの間の距離の関係を表したものです。
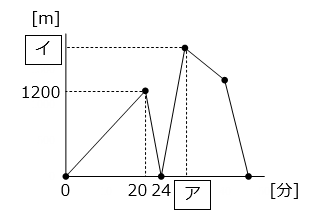
- ヒント
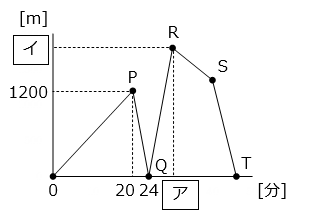
P:A さんが折り返し地点に到着
Q:A さんと B さんがすれ違う
R:B さんが折り返し地点に到着
S:A さんがゴールした
T:B さんがゴールした
(1)B さんの行きの速さを求めなさい。
- 答え(1)
- 分速 120 m
- 解説(1)
- グラフより、A さんは 20 分で折り返し地点に到着したことがわかるので、A さんの速さは 3600 ÷ 20 = 180 [m/分] である。
B さんの行きの速さを □ m/分とすると、
( 180 – □ ) × 20 = 1200
180 – □ = 60
□ = 120 [m/分]
(2)グラフ中の \(\boxed{ア}\) と \(\boxed{イ}\) に当てはまる数を求めなさい。
- 答え(2)
- \(\boxed{ア}\):30 \(\boxed{イ}\):1800
- 解説(2)
- \(\boxed{ア}\) は、B さんが折り返し地点に到着した時間なので、
\(\boxed{ア}\) = 3600 ÷ 120 = 30 [分]
\(\boxed{イ}\) は、B さんが折り返し地点に到着したときの A さんとの距離
B さんが折り返し地点に到着したのは A さんが折り返し地点に到着してから 30 – 20 = 10 [分後] より、
\(\boxed{イ}\) = 180 × 10 = 1800 [m]
(3)B さんの帰りの速さを求めなさい。
- 答え(3)
- 分速 225 m
- 解説(3)
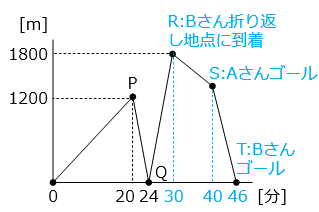
A さんは行きも帰りも同じ速さで走っていたので、ゴールしたのは 40 分後である。よって、B さんがゴールしたのは 40 + 6 = 46 [分後] となる。B さんが帰りにかかった時間は、46 – 30 = 16 [分] より、
3600 ÷ 16 = 225 [m/分]






