算数【入試】時計算

問１

時計の長針と短針がちょうど10時24分を指しているとき、時計の長針と短針が作る小さいほうの角の大きさは何度ですか。

答え

168度

解き方

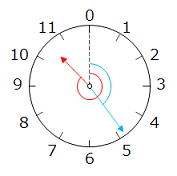
0時から時計回りに短針の角度は、360 × \(\dfrac{10}{12}\) + 360 × \(\dfrac{1}{12}\) × \(\dfrac{24}{60}\) = 312(度)
0時から時計回りに長針の角度は、360 × \(\dfrac{24}{60}\) = 144°
求める角度は、312 – 144 = 168°

問２

4時から4時30分の間で、長針と短針の角が10°となるのは2回あります。それぞれ4時何分になりますか。

答え

4時20分、4時23\(\dfrac{7}{11}\)分

解き方

4時のとき長針と短針は120°離れているので、長針と短針の角が10°になるためには、長針が短針に110°追いついたときと、130°追い越したときである。長針は1分間に6°、短針は1分間に0.5°動く。よって、追いつくまでにかかる時間は、110 ÷ (6 – 0.5) = 20(分)または、130 ÷ (6 – 0.5) = 23\(\dfrac{7}{11}\)(分)

問３

5時と6時の間で、長針が短針よりも70°先に進むのは5時何分ですか。

答え

5時40分

解き方

5時のとき長針と短針は150°離れているので、長針が短針よりも70°先に進むためには、長針が150 + 70 = 220°進めばよい。長針は1分間に6°、短針は1分間に0.5°動く。よって5時から、220 ÷ (6 – 0.5) = 40(分後)→5時40分

問４

時計が今、3時何分かを指しています。4分後には今の短針の位置に長針が来ます。今、3時何分ですか。

答え

3時12分

解き方

今から4分後に、今の短針に位置に長針が来ることから、今の長針と短針の角度は、6 × 4 = 24°。3時ちょうどのときの長針と短針の角度は90°なので、長針と短針の角度が90 – 24 = 66°小さくなるのは、3時から66 ÷ (6 – 0.5) = 12(分後)→3時12分

問５

ある日の午前0時ちょうどから時計の長針と短針の間が90°となるときを考えました。

(1) 7回目に長針と短針の間が90°となるのは午前何時何分ですか。

(2) この日の午後0時までに長針と短針の間が90°となることは何回ありますか。

答え(1)

午前3時32\(\dfrac{8}{11}\)分

答え(2)

22回

解き方(1)

長針と短針の間が90°となるのは、1回目は両針が動いた角度の差が90°になったときで、2回目以降は両針が動いた角度の差が180°になるごとである。よって、
(90 + 180 × 6) ÷ (6 – 0.5) = 212\(\dfrac{8}{11}\)(分後) → 午前3時32\(\dfrac{8}{11}\)分

解き方(2)

1回目は、90 ÷ (6 – 0.5) = 16\(\dfrac{4}{11}\)(分後)
2回目以降は、16\(\dfrac{4}{11}\) × 2 = 32\(\dfrac{8}{11}\)(分ごと)
よって、1回目以降の回数は、
(12 × 60 – 16\(\dfrac{4}{11}\)) ÷ 32\(\dfrac{8}{11}\) = 21\(\dfrac{1}{2}\) (21回)
したがって、22回