算数【基本】通過算

問１

（１）時速 96 kmで走る列車が、長さ 480 m のトンネルを 27 秒かかって通過します。この列車の長さは何 m ですか。

答え（１）: 240 m

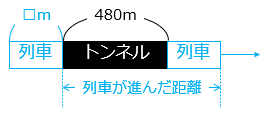
解き方（１）: 列車がトンネルを通過するために進んだ距離は、トンネルと列車の長さの和となる。
単位をそろえるために、時速 km から秒速 m に変換する
96 [km/時] = \(\dfrac{96\ ×\ 1000}{60\ ×\ 60}\) = \(\dfrac{80}{3}\) [m/秒]
27 秒で進む距離は
\(\dfrac{80}{3}\) × 27 = 720
720 – 480 = 240 [m]

（２）長さ 200 m の列車が、長さ 2200 m の橋を渡りはじめてから渡り終えるまで 80 秒かかりました。この列車の速さは、時速何 km ですか。

答え（２）: 時速 108 km

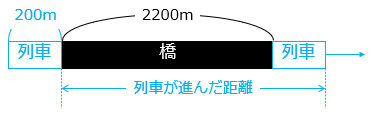
解き方（２）: 列車が橋を渡りはじめてから渡り終えるために進んだ距離は、列車と橋の長さの和となるので、200 + 2200 = 2400 [m]
よって、列車の速さは、
2400 ÷ 80 = 30 [m/秒] = 30 × 60 × 60 ÷ 1000 = 108 [km/時]

（３）長さ 216 mの列車が、トンネルの直前からトンネル内にすべて入るのに 6 秒かかります。列車の速さは秒速何 m ですか。

答え（３）: 秒速 36 m

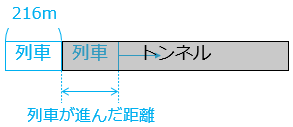
解き方（３）: 列車が進んだ距離は列車の長さである。
よって列車の速さは、
216 ÷ 6 = 36 [m/秒]

（４）時速 80 km で走る長さ 240 m の列車が 960 m の鉄橋を渡りはじめてから渡り終えるまでにかかる時間は何秒ですか。

答え（４）: 54 秒

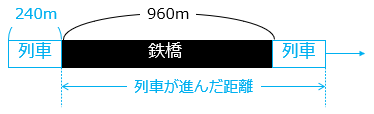
解き方（４）: 列車が進んだ距離は鉄橋と列車の長さの和 960 + 240 = 1200 [m] である。
時速80km = 秒速\(\dfrac{200}{9}\) m
よってかかる時間は、
1200 ÷ \(\dfrac{200}{9}\) = 54 [秒]

（５）長さ 150 m の電車が時速 54 km で走っています。この電車が 600 m の鉄橋を渡るとき、電車全体が鉄橋に乗っている時間は何秒ですか。

答え（５）: 30 秒

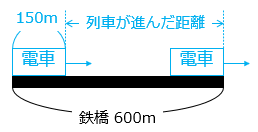
解き方（５）: 電車が鉄橋に乗っている間に進んだ距離は 600 – 150 = 450 [m]
時速54km = \(\dfrac{54\ ×\ 1000}{60\ ×\ 60}\) = 15 [m/秒]
よってかかる時間は、
450 ÷ 15 = 30 [秒]

（６）電柱の前を 24 秒で通り過ぎた列車が、長さ 1800 m のトンネルに入ります。列車の先頭がトンネルに入ってから、列車がトンネルの外に完全に出るまでに 1 分 36 秒かかりました。この列車の速さは秒速何 m ですか。

答え（６）: 秒速 25 m

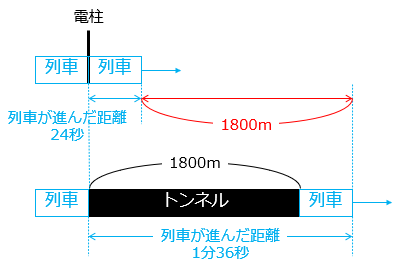
解き方（６）: 1 分 36 秒 = 96 秒
列車の先頭の移動を考えると、96 – 24 = 72 [秒] で、1800 m 進むことになる。
よって速さは、
1800 ÷ 72 = 25 [m/秒]

問２

2 つの列車のすれ違いと追いこし: ● 2 つの列車がすれ違う = それぞれの列車の最後尾が出会う

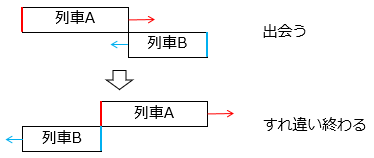
● 前の列車を追いこす = 前の列車 ( A ) の先頭に、後ろから来た列車 ( B ) の最後尾が追いつく

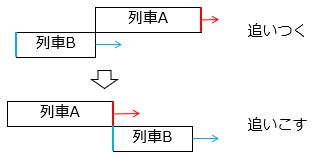
※旅人算として考えることができる

（１）長さが 160 m で時速 72 kmで走る上り列車と、長さが 240 m で分速 1.8 kmで走る下り列車が、すれちがうのに何秒かかりますか。

答え（１）: 8 秒

解き方（１）: 2 つの列車がすれ違う = それぞれの列車の最後尾が出会う
特急列車 A と B がすれ違い始めたときの A と B の最後尾の距離は、2 つの列車の長さの和に等しい。
72 [km/時] = \(\dfrac{72\ ×\ 1000}{60\ ×\ 60}\) = 20 [m/秒]
1.8 [km/分] = \(\dfrac{1.8\ ×\ 1000}{60}\) = 30 [m/秒]
よって、
( 160 + 240 ) ÷ ( 20 + 30 )
= 400 ÷ 50 = 8 [秒]

（２）時速 162 kmで走る特急列車 A と時速 108 km で走る特急列車 B が反対方向に向かって走っています。特急列車 A と特急列車 B がすれ違うのにかかった時間は 5 秒でした。特急列車 A の長さが 215 m のとき、特急列車 B の長さは何 m ですか。

答え（２）: 160 m

解き方（２）: 2 つの列車がすれ違う = それぞれの列車の最後尾が出会う
特急列車 A と B がすれ違い始めたときの A と B の最後尾の距離は、2 つの列車の長さの和に等しい。
162 [km/時] = \(\dfrac{162\ ×\ 1000}{60\ ×\ 60}\) = 45 [m/秒]
108 [km/時] = \(\dfrac{108\ ×\ 1000}{60\ ×\ 60}\) = 30 [m/秒]
特急列車 A と B の長さは、
( 45 + 30 ) × 5 = 375 [m]
したがって、B の列車の長さは、
375 – 215 = 160 [m]

（３）長さ 60 m で毎秒 20 mで走る普通電車と、長さ 120 m で毎秒 25 m で走る特急電車が、同じ向きに走っています。特急電車が普通電車を追いこし始めてから追いこし終わるまでにかかる時間は何秒ですか。

答え（３）: 36 秒

解き方（３）: 特急電車が普通電車を追いこす = 普通電車の先頭に、特急電車の最後尾が追いつく
特急列車と普通電車がすれ違い始めたときの、特急電車の最後尾と普通電車の先頭の距離は、2 つの列車の長さの和に等しい。
( 60 + 120 ) ÷ ( 25 – 20 )
= 180 ÷ 5 = 36 [秒]