算数【入試】通過算
問1
90km離れた2駅から列車Aと列車Bが向かい合って同時に出発します。この2つの列車A、Bは出発してからすれ違い終わるまでに、30分8秒かかります。列車Aの長さを185m、列車A、列車Bの速さをそれぞれ80km/時、100km/時とします。
(1) 列車A、Bが出会うまでの時間を求めなさい。
(2) 列車Bの長さを求めなさい。
(3) 2駅間に600mのトンネルがあります。列車Bがトンネルを通り抜けたのは駅を出発してから21分後でした。列車Aがトンネルを通り抜けるのは駅を出発してから何分後ですか。
- 答え(1)
- 30分
- 答え(2)
- 215m
- 答え(3)
- 42分後
- 解き方(1)
- \(\dfrac{90}{80+100}=\dfrac{1}{2}\)(時間) = 30(分)
- 解き方(2)
- (1)より、2つの列車がすれ違っている時間は8秒とわかる。その間に進んだ距離が2つの列車の和となる。よって列車Bの長さは、
\((\dfrac{80\times1000}{60}+\dfrac{100\times1000}{60})\times\dfrac{8}{60}-185=215\)(m)
- 解き方(3)
- 列車Bが21分間で進んだ距離(m)は、\(\dfrac{100\times1000}{60}\times21=35000\)(m)
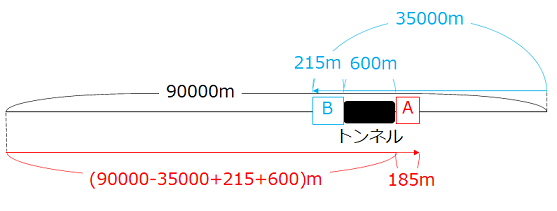
図より、列車Aがトンネルを通り抜けるために必要な距離は56000mである。よって必要な時間は、
\(56000\div\dfrac{80\times1000}{60}=42\)(分後)
問2
踏切A、B、Cが150m間隔であります。各踏切りの警報機は電車の先頭が通る20秒前から鳴り始め、最後尾が通り過ぎた3秒後に鳴り終わります。踏切Bの近くで2台の電車がすれ違いました。この2台の電車について「踏切A、B、Cの警報機が鳴っている時間」を太線の長さとして記録すると、図のようになりました。ただし、電車の長さは25m、速さは一定とし、踏切の幅は考えないものとします。
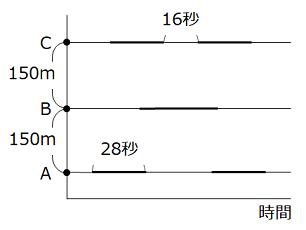
(1) 電車の速さは毎秒何mですか。
(2) 踏切Bの警報機は何秒なっていましたか。
- 答え(1)
- 毎秒5m
- 答え(2)
- 44秒間
- 解き方(1)
- 警報機は電車1台に対し28秒鳴り続けるが、電車が踏切を通過している時間は5秒である。よって、\(\dfrac{25}{5}\) = 5(m/秒)となる。
- 解き方(2)
- 踏切AからCに向かう電車を電車a、踏切CからAに向かう電車を電車cとし、それぞれの電車の位置を考える。
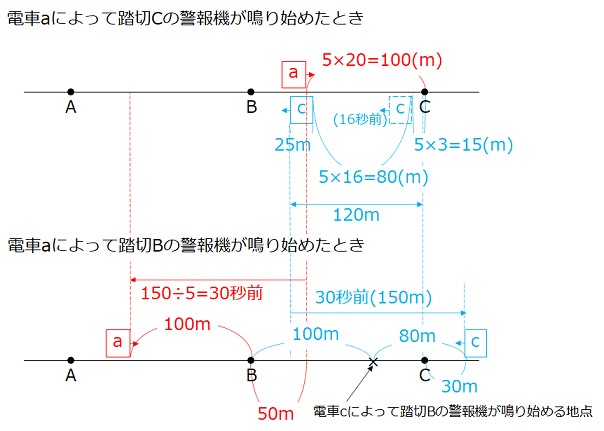
電車aによって踏切Cの警報機が鳴り始めるのは、電車aが踏切Cの手前100mに来たときである。この16秒前に、電車cは踏切Cから15m離れた地点にいたことになるため、このとき電車cはさらに80m離れた地点にあり、先頭は踏切Cより120mの地点にある。
電車aによって踏切Bの警報機が鳴り始めるのは、電車aによって踏切Cの警報機が鳴り始める地点より150m前、すなわち30秒前である。このとき電車cは、踏切Cの手前30mの地点にいる。踏切Bの警報機が電車cによって鳴り始めるのは、電車aによって警報機が鳴らされてから、80 ÷ 5 = 16(秒後)なので、警報機Bが鳴っている時間は28 + 16 = 44(秒間)である。
問3
ある電車が540mの鉄橋を渡りはじめてから渡り終わるまでに44秒かかります。また、この電車は同じ速さで2580mのトンネルに入りはじめてから完全に出るまでに3分かかります。電車の長さは何mですか。ただし、電車は一定の速さで走っているものとします。
- 答え
- 120m
- 解き方
- 電車が1秒間に進む距離を<1>とする。
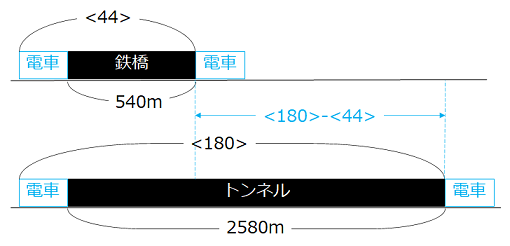
図より、
<180> – <44> = 2580 – 540
<1> = 15(m)
よって電車の長さは、
15 × 44 – 540 = 120(m)
問4
A、B、Cの列車があり、それぞれの長さが50m、80m、140mです。AがBに追いついてから完全に追いこすまでにかかる時間は20秒でした。また、CがBに追いついてから完全に追いこすまでにかかる時間は10秒でした。Cの速さがAの速さの1.5倍のとき、Cの速さは秒速何mですか。
- 答え
- 秒速46.5m
- 解き方
- AがBを追いこすのに20秒かかるので、AはBよりも、(50 + 80) ÷ 20 = 6.5(m/秒)速く進む。また、CがBを追いこすのに10秒かかるので、CはBよりも、(80 + 140) ÷ 10 = 22(m/秒)速く進む。Aの速さを<1>とすると、CとAの速さの差は、
<1.5> – <1> = 22 – 6.5 = 15.5(m/秒)
よって、Cの速さは<1.5> = 46.5(m/秒)
問5
列車Aと6両からなる列車Bがあり、この2つの列車はすれ違うのに5秒かかり、列車Bが列車Aを追い抜くのに65秒かかります。また、トンネルに入りはじめてから完全に抜け出すまでに列車Aは37秒かかり、列車Bは28秒かかります。また、列車Bの1両分の長さのバスが、線路と平行な道路を秒速15mで走っていたところ、「列車Aとバスがすれ違うのにかかる時間」と「同じ方向に進む列車Bとバスの先頭が並んでから最後尾が並ぶまでにかかる時間」が同じになりました。
(1) 列車Aと列車Bの速さの比を求めなさい。
(2) 列車Aと列車Bの長さの比を求めなさい。
(3) 列車Bの速さは秒速何mですか。
(4) トンネルの長さは何mですか。
- 答え(1)
- 6 : 7
- 答え(2)
- 7 : 3
- 答え(3)
- 毎秒28m
- 答え(4)
- 594m
- 解き方(1)
- 速さの和 : 速さの差 = \(\dfrac{1}{5}\) : \(\dfrac{1}{65}\) = 13 : 1
列車Aより列車Bのほうが速いので、AとBの速さの比は、
(13 – 1) : (13 + 1) = 6 : 7
- 解き方(2)
- まず2つの列車の長さの和を求める。列車Aと列車Bの速さをそれぞれ毎秒<6>、毎秒<7>とすると、2つの列車がすれ違うのに5秒かかることから、長さの和は、(<6> + <7>) × 5 = <65>となる。
次に2つの列車の長さの差を求める。
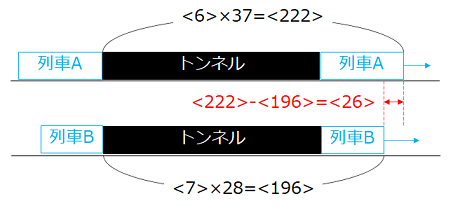
図より、2つの列車の長さの差は<26>となる。よって、列車Aと列車Bの長さの比は、(65 + 26) : (65 – 26) = 7 : 3
- 解き方(3)
- 列車Bの長さを<6>とすると、バスの長さは<1>、列車Aの長さは<6> × \(\dfrac{7}{3}\) = <14>となる。よって、列車Aとバスがすれ違うとき、列車Aとバスは<14> + <1> = <15>進む。また、列車Bとバスが進んだ道のりの差は<6> – <1> = <5>になる。この2つにかかる時間が等しいことから、列車Aとバスの速さの和と、列車Bとバスの速さの差の比は、<15> : <5> = 3 : 1
よって、列車Aと列車Bの速さをそれぞれ毎秒<6>、<7>とすると、
(<6> + 15) : (<7> – 15) = 3 : 1
<1> = 4(m/秒)
列車Bの速さ<7> = 28(m/秒)
- 解き方(4)
- 列車Aの速さは、<6> = 24(m/秒)((3)より)なので、列車AとBの長さの和は、(24 + 28) × 5 = 260(m)
よって、列車Bの長さは260 × \(\dfrac{3}{10}\) = 78(m)、列車Bとトンネルの長さの和は24 × 28 = 672(m)
したがって、トンネルの長さは672 – 78 = 594(m)





