算数【入試】割合

問１

ある店では、商品 A と商品 B を毎月仕入れています。先月の仕入れ代金は 10000 円でしたが、今月は商品 A が 12 % 値上がりし、商品 B も 4 % 値上がりしたので、仕入れ代金が 10 % 高くなりました。このとき、先月の商品 A と商品 B の仕入れ代金は、それぞれいくらですか。

答え

商品 A：7500 円　商品 B：2500 円

解き方

もし今月、商品 A も B と同様に4%値上がりしたと考えると、今月の仕入代金は 10000 × 1.04 = 10400 [円] となる。
しかし、実際の今月の仕入れ代金は 10000 × 1.1 = 11000 [円] だったので、この差の 11000 – 10400 = 600 [円] が、先月の商品 A の仕入れ代金の 12 – 4 = 8 [%] にあたる。
よって、先月の商品 A の仕入れ代金は 600 ÷ 0.08 = 7500 [円] となり、商品 B の仕入れ代金は 10000 – 7500 = 2500 [円] となる。

問２

ある本を 1 日目に全体の \(\dfrac{1}{4}\) を読み、2 日目に残りの \(\dfrac{2}{5}\) より 6 ページ多く読み、3 日目は 2 日目の残りの \(\dfrac{1}{3}\) を読んだところ、14 ページ残りました。この本は全体で何ページありますか。

答え

60 ページ

解き方

最後に残った 14 ページは 2 日目の残りの 1 – \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\) にあたるので、2 日目に残ったページ数は 14 ÷ \(\dfrac{2}{3}\) = 21 [ページ] である。
本全体のページを 4 と 5 の最小公倍数 ⑳ とおくと、1 日目は ⑳ × \(\dfrac{1}{4}\) = ⑤ 読み、2 日目は ⑮ × \(\dfrac{2}{5}\) = ⑥ と 6 ページ読んだことになる。

線分図より、
⑳ – ( ⑤ + ⑥ ) = 6 + 21
⑨ = 27
① = 3
本全体のページは ⑳ = 20 × 3 = 60 [ページ] である。

問３

A 子さんは、持っていたお金の \(\dfrac{2}{7}\) を使って筆箱を買いました。次に、残りの \(\dfrac{3}{5}\) を使って洋服を買いました。その後、500 円のおこづかいをもらったので、いま持っているお金は初めに持っていたお金の \(\dfrac{5}{14}\) になりました。初めに持っていたお金はいくらでしたか。

答え

7000 円

解き方

最初に持っていたお金を 7 と 5 の最小公倍数 ㉟ とおくと、帽子は ㉟ × \(\dfrac{2}{7}\) = ⑩、洋服は ㉕ × \(\dfrac{3}{5}\) = ⑮ となる。
残りのお金に 500 円足した ㉟ – ( ⑩ + ⑮ ) + 500 が ㉟ × \(\dfrac{5}{14}\) になる。

よって、
⑩ + 500 = \(\dfrac{㉕}{2}\)
⑤ = 1000
㉟ = ⑤ × 7 = 1000 × 7 = 7000 [円]

問４

あるクラスでは、遊園地 U に行ったことのある生徒がクラス全体の 60 %、遊園地 D に行ったことのある生徒はクラス全体の 35 % でした。遊園地 U に行ったことのある生徒のうち、25 % は遊園地 D に行ったことがあり、その数は 6 人でした。遊園地 U にも遊園地 D にも行ったことのない生徒は何人ですか。

答え

8 人

解き方

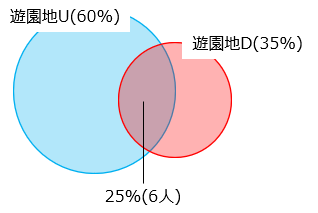
遊園地 U と D の両方に行ったことがある生徒は、クラス全体の 60 × 0.25 = 15 [%] となり、その人数は 6 人なので、クラス全体の人数は 6 ÷ 0.15 = 40 [人] である。
よって、遊園地 U に行ったことがある生徒は 40 × 0.6 = 24 [人]、遊園地 D に行ったことがある生徒は 40 × 0.35 = 14 [人] となる。
どちらの遊園地にも行ったことがない生徒は 40 – ( 24 + 14 – 6 ) = 8 [人] である。

問５

ある水そうに全体の \(\dfrac{3}{7}\) だけ水を入れました。そのうちの \(\dfrac{1}{3}\) を捨て、新たに 22 L の水を入れると水そう全体の \(\dfrac{3}{5}\) になりました。あと何 L の水を入れると満水になりますか。

答え

28 L

解き方

水そう全体に入る水の量を、7 と 5 の最小公倍数 ㉟ とおくと、最初に入れた水の量は ㉟ × \(\dfrac{3}{7}\) = ⑮ となる。
その \(\dfrac{1}{3}\) を捨てた後に残っている水の量は ⑮ × \(\dfrac{2}{3}\) = ⑩ となる。

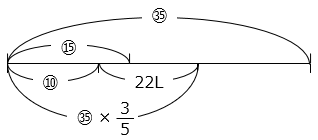
線分図より、
⑩ + 22 = ㉟ × \(\dfrac{3}{5}\) = ㉑
⑪ = 22
① = 2
となり、満水の水の量は ㉟ = 2 × 35 = 70 [L]、現在入っている水の量は 70 × \(\dfrac{3}{5}\) = 42 [L] である。
よって、満水にするためには 70 – 42 = 28 [L] の水が必要である。

問６

ある都市の 5 年前の人数と昨年の人数を比べました。昨年は男性も女性もどちらも 840000 人でした。5 年前にくらべて男性が 20 % 減少し、女性は 20 % 増加していました。

（１）5 年前の男性の人数は何人でしたか。

答え（１）

1050000 人

解き方（１）

5 年前の男性の人数は、昨年の 80 % となる。よって、
840000 ÷ 0.8 = 1050000 [人]

（２）昨年の人数は、5 年前に比べて何人増加、または何人減少しましたか。

答え（２）

70000 人減少

解き方（２）

昨年の人数は 840000 × 2 = 1680000 [人]。
5 年前の女性の人数は、840000 ÷ 1.2 = 700000 [人] となり、5 年前の人数は 1050000 + 700000 = 1750000 [人] である。
よって、昨年の人数は 5 年前より減少しており、その差は 70000 人である。