算数【入試】線分図（和差算・分配算・差集め算・過不足算）

問１

A 君、B 君、C 君の 3 人が 100 個のみかんを分けたところ、B 君は A 君の 2 倍を受け取り、C 君は A 君の \(\displaystyle\frac{2}{5}\) 倍よりも 15 個多く受け取りました。このとき、C 君の受け取ったみかんは何個ですか。

答え

25 個

解き方

A 君の受けっ取ったみかんの個数を ⑤ とすると、B 君が受け取ったみかんの個数は ⑤ × 2 = ⑩、C 君が受け取ったみかんの個数は ⑤ × \(\displaystyle\frac{2}{5}\) + 15 = ② + 15 と表すことができる。

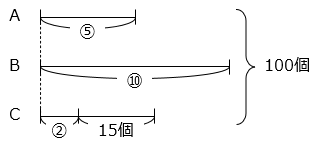
線分図より、次の式が成り立つ。
⑤ + ⑩ + ② = 100 – 15
⑰ = 85
① = 85 ÷ 17 = 5 [個]
よって、C 君が受け取ったみかんの個数は 2 × 5 + 15 = 25 [個]

問２

あめを 3 人で分けました。A 君は全体の \(\dfrac{1}{3}\)、B 君は全体の \(\dfrac{1}{7}\) と 7 個を取りました。すると、C 君のあめは B 君より 2 個多くなりました。C 君のあめは何個ですか。

答え

15個

解き方

あめ全体の個数を 3 と 7 の最小公倍数である ㉑ とすると、A 君は ㉑ × \(\dfrac{1}{3}\) = ⑦、B 君は ㉑ × \(\dfrac{1}{7}\) + 7 = ③ + 7、C 君は ③ + 7 + 2 = ③ + 9 と表すことができる。

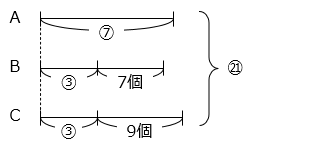
線分図より、次の式が成り立つ。
⑦ + ③ + 7 + ③ + 9 = ㉑
⑧ = 16
① = 2
よって、C 君のあめの個数は 3 × 2 + 9 = 15 [個]

問３

250 枚のカードを A 君、B 君、C 君の 3 人で分けたところ、B 君は A 君の \(\displaystyle\frac{3}{4}\) より 28 枚多く、C 君は B 君の \(\displaystyle\frac{5}{7}\) より 10 枚多くなりました。C 君はカードを何枚持っていますか。

答え

75枚

解き方

A 君のもらったカードの枚数を、4 と 7 の最小公倍数である \(\boxed{28}\) とすると、B 君がもらったカードの枚数は \(\boxed{28}\) × \(\displaystyle\frac{3}{4}\) + 28 = \(\boxed{21}\) + 28、C 君がもらったカードの枚数は ( \(\boxed{21}\) + 28 ) × \(\displaystyle\frac{5}{7}\) + 10 = \(\boxed{15}\) + 30 と表すことができる。

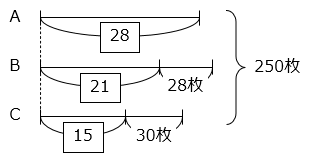
線分図より、次の式が成り立つ。
\(\boxed{28}\) + \(\boxed{21}\) + \(\boxed{15}\) = 250 – 28 – 30
\(\boxed{64}\) = 192
\(\boxed{1}\) = 192 ÷ 64 = 3 [枚]
よって、C 君がもらったカードの枚数は 15 × 3 + 30 = 75 [枚]

問４

和が 224 の 3 つの数字 A、B、C があります。B は A の 3 倍より 11 大きく、C は A の 4 倍より 21 大きいとき、B はいくつですか。

答え

83

解き方

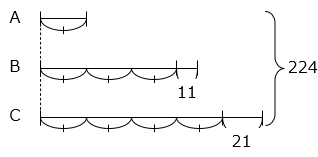
線分図より、次の式が成り立つ。
8 × A = 224 – 11 – 21 = 192
A = 192 ÷ 8 = 24
よって、B = 24 × 3 + 11 = 83