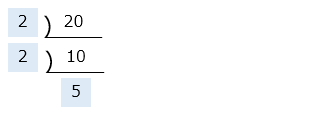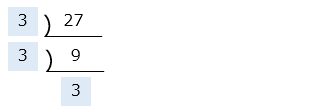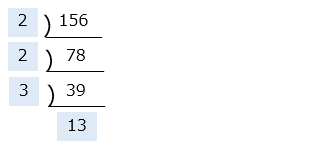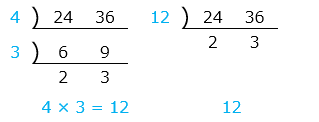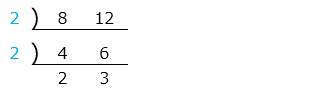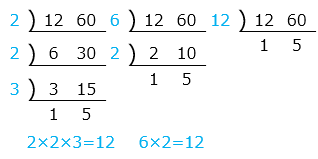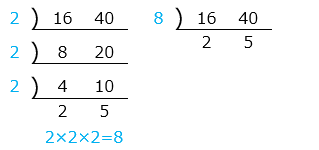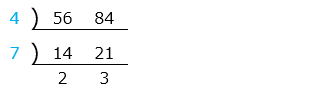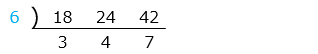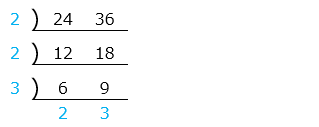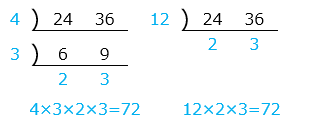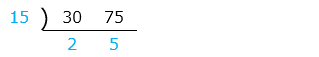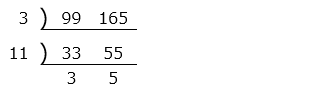算数【基本】約数・倍数・素数
問1 約数(公約数・最大公約数)・素数
(1)次の数の約数をすべて書きなさい。
- 約数とは
- ある整数を割り切ることができる整数
●「1」はすべての整数の約数である
●ある整数の約数には、その整数自身も含まれる
●ある整数をその約数で割ると、その商もある整数の約数である
① 3 ② 26 ③ 49 ④ 84 ⑤ 100
- 答え(1)- ①, ②, ③, ④, ⑤
- ① 1, 3
② 1, 2, 13, 26
③ 1, 7, 49
④ 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
⑤ 1, 2, 4, 5, 10, 20, 25, 50, 100
- 解き方(1)- ①, ②, ③, ④, ⑤
- 「ある整数をその約数で割ると、その商もある整数の約数である」を利用する
① 3 ÷ 1 = 3
② 26 ÷ 1 = 26, 26 ÷ 2 = 13、26 ÷ 3 割り切れない、26 ÷ 4 割り切れない、26 ÷ 5 割り切れない、26 ÷ 6 割り切れない、26 ÷ 7 割り切れない、26 ÷ 8 割り切れない、26 ÷ 9 割り切れない、26 ÷ 10 割り切れない、26 ÷ 11 割り切れない、26 ÷ 12 割り切れない
③ 49 ÷ 1 = 49、49 ÷ 2 割り切れない、49 ÷ 3 割り切れない、49 ÷ 4 割り切れない、49 ÷ 5 割り切れない、49 ÷ 6 割り切れない、49 ÷ 7 = 7
④
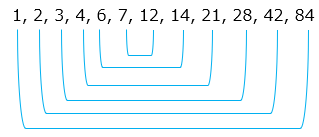
⑤
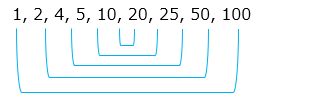
(2)1 ~ 20 までの整数のうち、素数をすべて書きなさい。
- 素数とは
- 約数が「1」と「その数自身」しかない整数
●「0」「1」は素数ではない
- 答え(2)
- 2, 3, 5, 7, 11, 13, 17, 19
- 解き方(2)
- 1 → 素数ではない
2の約数 1, 2 → 素数
3の約数 1, 3 → 素数
4の約数 1, 2, 4 → 素数ではない
5の約数 1, 5 → 素数
6の約数 1, 2, 3, 6 → 素数ではない
7の約数 1, 7 → 素数
8の約数 1, 2, 4, 8 → 素数ではない
9の約数 1, 3, 9 → 素数ではない
10の約数 1, 2, 5, 10 → 素数ではない
11の約数 1, 11 → 素数
12の約数 1, 2, 3, 4, 6, 12 → 素数ではない
13の約数 1, 13 → 素数
14の約数 1, 2, 7, 14 → 素数ではない
15の約数 1, 3, 5, 15 → 素数ではない
16の約数 1, 2, 4, 8, 16 → 素数ではない
17の約数 1, 17 → 素数
18の約数 1, 2, 3, 6, 9, 18 → 素数ではない
19の約数 1, 19 → 素数
20の約数 1, 2, 4, 5, 10, 20 → 素数ではない
(3)次の数を素因数分解しなさい。
- 素因数分解とは
- 整数を素数のかけ算で分解し表すこと。
【素因数分解の方法「連除法(すだれ算)」】
12 を素因数分解すると
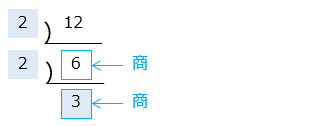
図のように、割り切ることができる素数で商が素数になるまで割っていく。
すべての素数をかける ⇒ 2 × 2 × 3
① 9
- 答え(3)- ①
- 3 × 3
- 解き方(3)- ①

② 15
- 答え(3)- ②
- 3 × 5
- 解き方(3)- ②

③ 20
- 答え(3)- ③
- 2 × 2 × 5
- 解き方(3)- ③
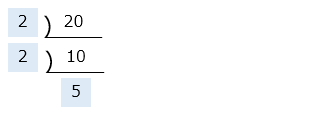
④ 27
- 答え(3)- ④
- 3 × 3 × 3
- 解き方(3)- ④
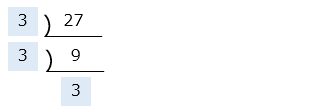
⑤ 156
- 答え(3)- ⑤
- 2 × 2 × 3 × 13
- 解き方(3)- ⑥
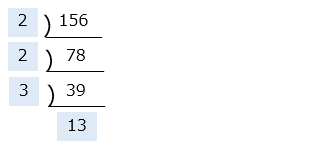
(4)次の数の公約数と最大公約数を求めなさい。
- 公約数と最大公約数とは
- 公約数:2 つ以上の整数に共通する約数
最大公約数:公約数のうち最も大きい数
●公約数には必ず「1」が含まれる
●公約数は最大公約数の約数である
【最大公約数の求め方「連除法(すだれ算)」】
24 と 36 の最大公約数を求める

図のように、2 つの数を割り切ることができる共通の数(青字)で、割り切れる共通の数がなくなるまで割っていく。それまでに割った共通の数(青字)の積が最大公約数となる。
24 と 36 の最大公約数は 2 × 2 × 3 = 12
※はじめから大きい数で割ることで、式を短くできる。
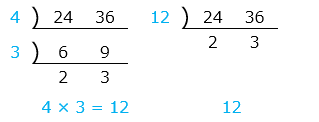
① 8, 12
- 答え(4)- ①
- 公約数 1, 2, 4
最大公約数 4
- 解き方(4)- ①
- 最大公約数を求める。
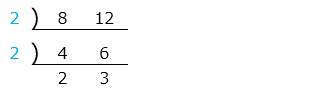
青字(共通の約数)の積、2 × 2 = 4 が最大公約数となる。
公約数は最大公約数の約数なので、1, 2, 4
② 12, 60
- 答え(4)- ②
- 公約数 1, 2, 3, 4, 6, 12
最大公約数 12
- 解き方(4)- ②
- 最大公約数を求める。
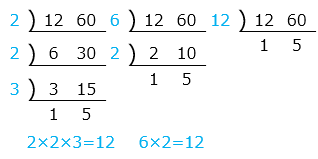
青字(共通の約数)の積、12 が最大公約数となる。
公約数は最大公約数の約数なので、1, 2, 3, 4, 6, 12
③ 16, 40
- 答え(4)- ③
- 公約数 1, 2, 4, 8
最大公約数 8
- 解き方(4)- ③
- 最大公約数を求める。
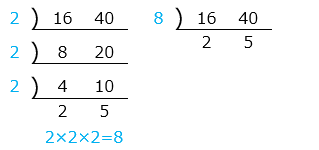
青字(共通の約数)の積、8 が最大公約数となる。
公約数は最大公約数の約数なので、1, 2, 4, 8
④ 56, 84
- 答え(4)- ④
- 公約数 1, 2, 4, 7, 14, 28
最大公約数 28
- 解き方(4)- ④
- 最大公約数を求める。
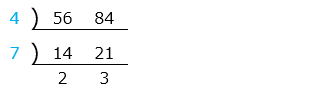
青字(共通の約数)の積、7 × 4 = 28 が最大公約数となる。
公約数は最大公約数の約数なので、1, 2, 4, 7, 14, 28
⑤ 18, 24, 42
- 答え(4)- ⑤
- 公約数 1, 2, 3, 6
最大公約数 6
- 解き方(4)- ⑤
- 最大公約数を求める。
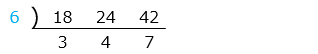
青字(共通の約数)の積、6 が最大公約数となる。
公約数は最大公約数の約数なので、1, 2, 3, 6
問2 倍数(公倍数・最小公倍数)
(1)次の数の倍数を小さい方から順に 3 個書きなさい。
- 倍数とは
- ある整数を 1 倍、2 倍、3 倍、・・・した数
●0 倍した数( = 0 )は倍数には含まない。
●ある整数の倍数は、ある整数で割り切れる。
① 4 ② 11 ③ 90
- 答え(1)- ①, ②, ③
- ① 4, 8, 12
② 11, 22, 33
③ 90, 180, 270
- 解き方(1)- ①, ②, ③
- ① 4 × 1 = 4, 4 × 2 = 8, 4 × 3 = 12
② 11 × 1 = 11, 11 × 2 = 22, 11 × 3 = 33
③ 90 × 1 = 90, 90 × 2 = 180, 90 × 3 = 270
(2)23 の小さい方から 15 番目の倍数を答えなさい。
- 答え(2)
- 345
- 解き方(2)
- ある整数 A の小さい方から □ 番目の数は、A × □ で求められる。
よって、23 × 15 = 345
(3)A ~ J の整数があります。以下の問いに答えなさい。
A. 12 B. 48 C. 65 D. 80 E. 91
F. 518 G. 1024 H. 5888 I. 12300 J. 642642
- ヒント(3)
- 2 の倍数:一の位が偶数
3 の倍数:各位の数字の和が3の倍数
4 の倍数:下 2 けたが 4 の倍数、または下 2 けたが 00
5 の倍数:一の位が 0 または5
6 の倍数:偶数かつ 3 の倍数
8 の倍数:下 3 けたが 8 の倍数、または下 3 けたが 000
9 の倍数:各位の数字の和が 9 の倍数
※けた数が大きい数について判断するとき、知っていると便利です!
① 2 の倍数をすべて選びなさい。
- 答え(3)- ①
- A, B, D, F, G, H, I, J
- 解き方(3)- ①
- 一の位が偶数の数を選ぶ → A. 12, B. 48, D. 80, F. 518, G. 1024, H. 5888, I. 12300, J. 642642
② 3 の倍数をすべて選びなさい。
- 答え(3)- ②
- A, B, I, J
- 解き方(3)- ②
- 各位の数字の和が 3 の倍数になる数を選ぶ
A. 1 + 2 = 3
B. 4 + 8 = 12 = 3 × 4
C. 6 + 5 = 11
D. 8 + 0 = 8
E. 9 + 1 = 10
F. 5 + 1 + 8 = 14
G. 1 + 0 + 2 + 4 = 7
H. 5 + 8 + 8 + 8 = 29
I. 1 + 2 + 3 + 0 + 0 = 6 = 3 × 2
J. 6 + 4 + 2 + 6 + 4 + 2 = 24 = 3 × 8
③ 8 の倍数をすべて選びなさい。
- 答え(3)- ③
- B, D, G, H
- 解き方(3)- ③
- 8 で割り切れる、または下 3 けたが 8 の倍数、または下 3 けたが 000 を選ぶ
A. 12 ÷ 8 ・・・割り切れない
B. 48 ÷ 8 = 6
C. 65 ÷ 8 ・・・割り切れない
D. 80 ÷ 8 = 10
E. 91 ÷ 8 ・・・割り切れない
F. 518 ÷ 8 ・・・割り切れない
G. 024 ÷ 8 = 3
H. 888 ÷ 8 = 111
I. 300 ÷ 8 ・・・割り切れない
J. 642 ÷ 8 ・・・割り切れない
(4)250 に最も近い 9 の倍数を求めなさい。
- 答え(4)
- 252
- 解き方(4)
- 250 以下で 250 に最も近い 9 の倍数は、9 と 250 を 9 で割った商の積で求められる。
250 ÷ 9 = 27 あまり 7 より、250 以下で 250 に最も近い 9 の倍数は 9 × 27 = 243
次に大きい 9 の倍数は 9 × 28 = 252
250 に最も近い 9 の倍数は 252
(5)次の数の最小公倍数を求めなさい。
- 公倍数と最小公倍数とは
- 公倍数:2 つ以上の整数に共通する倍数
最小公倍数:公倍数のうち最も小さい数
●公倍数は最小公倍数の倍数である
【最小公倍数の求め方「連除法(すだれ算)」】
① 24 と 36 の最小公倍数を求める
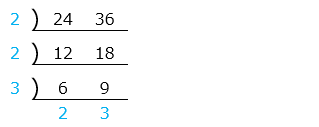
図のように、2つの数を割り切ることができる共通の数(青字)で、割り切れる共通の数がなくなるまで割っていく。それまでに割った共通の数と最後の商(青字)の積が最小公倍数となる。
24 と 36 の最小公倍数は 2 × 2 × 3 × 2 × 3 = 72
※はじめから大きい数で割ることで、式を短くできる。
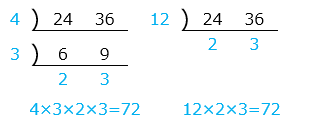
② 24 と 36 と 48 の最小公倍数を求める
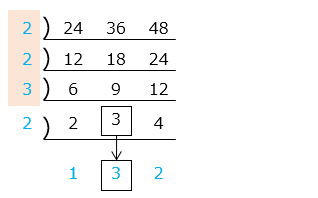
3つの商のうち2つが共通の数で割り切れるときはわり算を続け、割り切れない商はそのまま下ろす。それまでに割った共通の数と最後の商(青字)の積が最小公倍数となる。
24 と 36 と 48 の最小公倍数は、2 × 2 × 3 × 2 × 1 × 3 × 2 = 144
※このとき、最大公約数は3 つとも割り切れる数のみかけあわせる。
24 と 36 と 48 の最大公約数は、2 × 2 × 3 = 12
① 6, 9
- 答え(5)- ①
- 18
- 解き方(5)- ①

青字(割った数と最後の商)の積が最小公倍数なので、3 × 2 × 3 = 18
② 15, 18
- 答え(5)- ②
- 90
- 解き方(5)- ②

青字(割った数と最後の商)の積が最小公倍数なので、3 × 5 × 6 = 90
③ 30, 75
- 答え(5)- ③
- 150
- 解き方(5)- ③
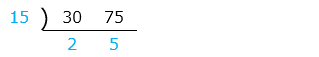
青字(割った数と最後の商)の積が最小公倍数なので、15 × 2 × 5 = 150
④ 4, 12, 18
- 答え(5)- ④
- 36
- 解き方(5)- ④
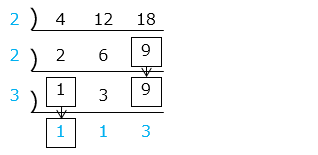
青字(割った数と最後の商)の積が最小公倍数なので、2 × 2 × 3 × 1 × 1 × 3 = 36
⑤ 16, 24, 48
- 答え(5)- ⑤
- 48
- 解き方(5)- ⑤
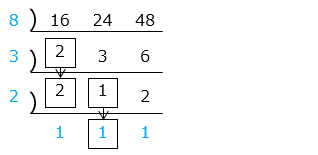
青字(割った数と最後の商)の積が最小公倍数なので、8 × 3 × 2 × 1 × 1 × 1 = 48
問3
縦 180 cm、横 240 cmの紙があります。この紙をあまりがでないように大きさの等しい正方形に切り分けます。切り分ける正方形を最も大きくなるようにするとき、全部で何枚に分けることができますか。
- 答え
- 12 枚
- 解き方
- 最も大きい正方形に切り分けるとき、その1辺の長さは 180 と 240 の最大公約数 60 [cm] となる。したがって、切り分けられる正方形の枚数は、
( 180 ÷ 60 ) × ( 240 ÷ 60 ) = 3 × 4 =12 [枚]
問4
4 と 9 の両方で割れる数の中で 2000 に最も近い整数を求めなさい。
- 答え
- 2016
- 解き方
- 4 と 9 の両方でわれる数は、4 と 9 の最小公倍数である 36 の倍数である。
2000 以下で最も大きい 36 の倍数は、2000 ÷ 36 = 55 余り 20 より、36 × 55 = 1980
次に大きい数は、36 × 56 = 1980 + 36 = 2016
よって、2016
問5
10 以上 50 以下の整数の中で、6 で割り切れる数は何個ありますか。
- 答え
- 7 個
- 解き方
- 50 以下の整数で 6 で割り切れる数の個数は、50 ÷ 6 = 8. …より 8 個。
10 より小さい整数で 6 で割り切れる数の個数は、10 ÷ 6 = 1. …より 1 個。
よって、10 以上 50 以下の整数の中で、6 で割り切れる数の個数は、8 – 1 = 7 [個]
問6
整数 A について、A の約数の個数を<A>とします。例えば、<3> = 2、<10> = 4 となります。
- 便利な解法(約数の個数を求める方法)
- ある数の約数の個数は、
1.ある数を素因数分解する
2.得られた約数とその個数をまとめる
3.その個数に1を足し、それぞれかけ算する
実際にやってみましょう。
例 1:16 の約数の個数は?
16 を素因数分解すると、2 × 4 個となる。したがって 4 個 + 1 で答えは 5。
例 2:50 の約数の個数は?
50 を素因数分解すると、( 2 × 1 個 ) × ( 5 × 2 個 )となる。したがって(1 個 + 1 ) × ( 2 個 + 1 )で答えは 6。
例 3:2520 の約数の個数は?
2520 を素因数分解すると、( 2 × 3 個 ) × ( 3 × 2 個 ) × ( 5 × 1 個 ) × ( 7 × 1 個 )となる。したがって ( 3 個 + 1 ) × ( 2 個 + 1 ) × ( 1 個 + 1 ) × ( 1 個 + 1 )で、4 × 3 × 2 × 2 となり答えは 48。
(1)<18>を求めなさい。
- 答え(1)
- 6
- 解き方(1)
- 18 の約数は、1、2、3、6、9、18 より、6 個
(2)<100>を求めなさい。
- 答え(2)
- 9
- 解き方(2)
- 100 の約数は、1、2、4、5、10、20、25、50、100 より、9 個
(3)A が 2 けたの整数のとき、<A>が奇数となる A は何個ありますか。
- 答え(3)
- 6 個
- 解き方(3)
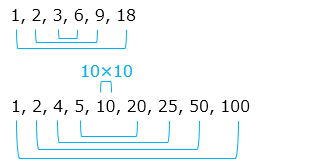
図のように、ある整数の約数を順番に並べると、左から 1 番目と右から 1 番目をかける、左から 2 番目と右から 2 番目をかける、・・・とある整数になる。そして、ある整数が 100 のように同じ数の積 ( 10 × 10 ) となる場合、その約数の個数は奇数となる。
2 けたの整数の中で同じ数の積になっているのは、16、25、36、49、64、81 の 6 個
問7
2 の倍数であり 7 の倍数である数の中で、5 番目に小さい数を求めなさい。
- 答え
- 70
- 解き方
- 2 の倍数であり 7 の倍数である数は、2 と 7 の最小公倍数である 14 の倍数である。
よって、14 × 5 = 70
問8
156 を割ると 6 あまるような整数は何個ありますか。
- 答え
- 7 個
- 解き方
- 156 を割ると 6 あまるような整数とは、156 からあまりの 6 を引いた 150 を割ると割り切れ、かつ 6 より大きい数である。すなわち、150 の約数で 6 より大きい数である。
150 の約数は、1、2、3、5、6、10、15、25、30、50、75、150
このうち 6 より大きい数は、7 個
問9
100 以下の数で 3 でも 5 でも割り切れる数のうち、6 で割ると 3 あまる数は何個ありますか。
- 答え
- 3 個
- 解き方
- 3 でも 5 でも割り切れる数は、3 と 5 の最小公倍数である 15 の倍数より、100 以下には、100 ÷ 15 = 6. …より 6 個ある。書き出すと、
15, 30, 45, 60, 75, 90
このうち、6 の倍数( 6で割り切れる数 )を除くと、15, 45, 75
15 ÷ 6 = 2 あまり 3
45 ÷ 6 = 7 あまり 3
75 ÷ 6 = 12 あまり 3
よって、3 個
問10
縦 1 cm、横 2 cmのタイルがたくさんあります。これらをすき間なく並べて正方形を作ります。
(1)考えられる正方形の中で、3 番目に小さい正方形を作るにはタイルは何枚必要ですか。
- 答え(1)
- 18 枚
- 解き方(1)
- 考えられる正方形の一辺の長さは、1 と 2 の最小公倍数である 2 の倍数となる。よって、3 番目に小さい正方形の一辺の長さは 2 × 3 = 6 [cm] である。
このときタイルは、縦に 6 ÷ 1 = 6 [枚]、横に 6 ÷ 2 = 3 [枚] 必要なので、全部で 6 × 3 = 18 [枚] 必要となる。
(2)タイルが 50 枚以上 100 枚以下あるとき、何種類の大きさの正方形ができますか。
- 答え(2)
- 3 種類
- 解き方(2)
- 4 番目に小さい正方形の一辺の長さは 2 × 4 = 8 [cm]、必要なタイルの枚数は 8 ÷ 1 × 8 ÷ 2 = 8 × 4 = 32 [枚]
5 番目に小さい正方形の一辺の長さは 2 × 5 = 10 [cm]、必要なタイルの枚数は 10 ÷ 1 × 10 ÷ 2 = 10 × 5 = 50 [枚]
6 番目に小さい正方形の一辺の長さは 2 × 6 = 12 [cm]、必要なタイルの枚数は 12 ÷ 1 × 12 ÷ 2 = 12 × 6 = 72 [枚]
7 番目に小さい正方形の一辺の長さは 2 × 7 = 14 [cm]、必要なタイルの枚数は 14 ÷ 1 × 14 ÷ 2 = 14 × 7 = 98 [枚]
7 番目に小さい正方形の一辺の長さは 2 × 8 = 16 [cm]、必要なタイルの枚数は 16 ÷ 1 × 16 ÷ 2 = 16 × 8 = 128 [枚]
よって、3 種類
問11
ある駅から、A 行きの電車が 13 分おきに、B 行きの電車が 26 分おきに、C 行きの電車が 12 分おきに出ています。どの電車も始発が午前 6 時のとき、次に同時に出発するのは午前何時何分ですか。
- 答え
- 午前 8 時 36 分
- 解き方
- 同時に出発するのは、13 と 26 と 12 の最小公倍数の値ごと
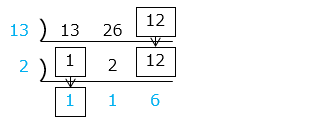
図より、最小公倍数は 13 × 2 × 6
次に同時に出発するのは、
13 × 2 × 6 [分後]
= 13 × 2 × 6 × \(\dfrac{1}{60}\) = \(2\dfrac{3}{5}\) [時間後]
= 2 時間 36 分後
よって、午前 8 時 36 分
問12
えんぴつが 108 本、消しゴムが 72 個あります。えんぴつと消しゴムをそれぞれ同じ数ずつ、あまりがでないように、できるだけ多くの子どもに配ります。何人の子どもに配ることができますか。
- 答え
- 36 人
- 解き方
- えんぴつと消しゴムをあまりが出ないように分ける最も大きい数は、108 と 72 の最大公約数 36 となる。よって、36 人。
問13
1 × 2 × 3 × 4 × 5 × ・・・ × 10 のように、1 から 10 までの整数をかけた数は、6 で何回割り切れますか。
- 答え
- 4 回
- 解き方
- 素数以外を素因数分解し、2 × 3 の個数(= 6で割り切れる回数)を求める。
1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10
= 1 × 2 × 3 × 2 × 2 × 5 × 2 × 3 × 7 × 2 × 2 × 2 × 3 × 3 × 2 × 5
2 は 8 個、3 は 4 個より、2 × 3 は 4 個、よって 4 回
問14
99 と 165 の最小公倍数と最大公約数を求めたとき、最小公倍数は最大公約数の何倍ですか。
- 答え
- 15 倍
- 解き方
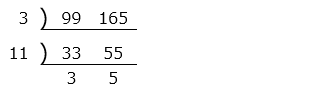
図より、最大公約数は 3 × 11、最小公倍数は 3 × 11 × 3 × 5 より、15 倍
問15
2 けたの整数 A について、2 で割ることのできる回数を<A>とします。例えば、<10>は 10 ÷ 2 = 5、5 は 2 で割り切れないので 1 です。また、<12>は 12 ÷ 2 = 6、6 ÷ 2 = 3 なので 2 です。<A>が 3 であるとき、最も大きい A の数を求めなさい。
- 答え
- 88
- 解き方
- 求める A は、素因数分解すると 2 × 2 × 2 × □( □ は奇数 )で表される数である。そのうち、2 けたの数で最も大きいのは、2 × 2 × 2 × 11 = 88
問16
\(\dfrac{14}{27}\) と \(\dfrac{7}{18}\) のどちらにかけても整数になる、一番小さい分数を求めなさい。
- ヒント
- \(\dfrac{A}{B}\) × \(\dfrac{△}{□}\) と \(\dfrac{C}{D}\) × \(\dfrac{△}{□}\) がともに整数となる最も小さい \(\dfrac{△}{□}\)
\(\dfrac{△}{□}\) = \(\dfrac{BとDの最小公倍数}{AとCの最大公約数}\)
- 答え
- \(7\dfrac{5}{7}\)
- 解き方
- 求める分数は、分子は 2 つの分数の分母である 27 と 18 の最小公倍数 54、分母は 2 つの分数の分子である 14 と 7 の最大公約数 7 となる。
\(\dfrac{54}{7}\) = \(7\dfrac{5}{7}\)
問17
縦 4 cm、横 8 cm、高さ 3 cmの直方体があります。この直方体を、同じ向きにすき間なく並べたり積んだりして、できるだけ小さい立方体をつくります。このとき、直方体は何個必要ですか。
- 答え
- 144 個
- 解き方
- できるだけ小さい立方体の一辺の長さは、4 と 8 と 3 の最小公倍数24 [cm] になる。
よって、縦は 24 ÷ 4 = 6 [個]、横は 24 ÷ 8 = 3 [個]、縦は 24 ÷ 3 = 8 [個] 必要なので、全部で 6 × 3 × 8 = 144 [個] 必要。
問18
30 未満の 4 の倍数をすべて足すといくつになりますか。
- 答え
- 112
- 解き方
- 30未満で最大の4の倍数は 4 × 7 = 28
4 × 1 + 4 × 2 + ・・・ + 4 × 7
= 4 × ( 1 + 2 + 3 + 4 + 5 + 6 + 7 )
= 4 × 28 = 112
問19
1512 の約数で、3 番目に大きい数を求めなさい。
- 答え
- 504
- 解き方
- 3 番目に小さい約数がわかると、3 番目に大きい約数もわかる。

問20
8 とある整数の最大公約数は 4、最小公倍数は 104 です。ある整数を求めなさい。
- 答え
- 52
- 解き方
- ある整数を □、ある整数を最大公約数の 4 で割った商を ○ とする。

図より、8 とある整数 □ の最小公倍数は、4 × 2 × ○ = 104
○ = 13
□ = 4 × ○ = 4 × 13 = 52
問21
縦が 3 cm、横が 4 cmのタイルがあります。面積が 576 cm2 の正方形になるようにタイルをしきつめるとき、縦には何個のタイルを並べればよいですか。
- 答え
- 8 個
- 解き方

576 = 4 × 12 × 12 = 2 × 2 × 12 × 12 = 24 × 24 より、
面積が 576 cm2 の正方形の一辺の長さは 24 cm
縦に必要なタイルは、24 ÷ 3 = 8 [個]
問22
1 から 100 までの数字で、6 の倍数に ○ をつけ、8 の倍数に □ をつけます。連続した 3 つの数字で、7 や 17 のように、○ と □ ではさまれた数字は何個ありますか。
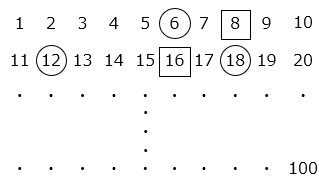
- 答え
- 8 個
- 解き方
- ○ と □ ではさまれた数は、6 の倍数より1大きく、8 の倍数より 1 小さい数である。6 の倍数より 1 大きく、8 の倍数より 1 小さい数で最も小さい数は7 で、それ以降は 6 と 8 の最小公倍数である 24 ごとに出てくるので、
7, 31, 55, 79 の 4 個
□ と ○ ではさまれた数は、8 の倍数より 1 大きく、6 の倍数より1小さい数である。8 の倍数より1大きく、6 の倍数より 1 小さい数で最も小さい数は 17 で、それ以降は 6 と 8 の最小公倍数である 24 ごとに出てくるので、
17, 41, 65, 89 の 4 個
よって、8 個