算数【応用】約数・倍数・素数

問１

70 とある数の最大公約数は 14、最小公倍数は 490 です。ある数を求めなさい。

答え

98

解き方

ある数を□とする。

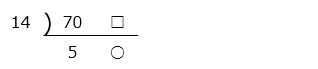
70 と□の最小公倍数は 14 × 5 × ○ と表すことができるので、
14 × 5 × ○ = 490
○ = 7
よって、
□ = 14 × ○ = 14 × 7 = 98

問２

ある数に \(\dfrac{7}{8}\) をかけても \(2\dfrac{4}{5}\) をかけても積は整数になります。このような数のうち、最も小さいものを答えなさい。

答え

\(5\dfrac{5}{7}\)

解き方

\(2\dfrac{4}{5}\) = \(\dfrac{14}{5}\) より、
ある数の分子は、5 と 8 の最小公倍数である 40
ある数の分母は、7 と 14 の最大公約数である 7
ある数は \(\dfrac{40}{7}\) = \(5\dfrac{5}{7}\)

問３

48 のすべての約数をたすと□です。□に当てはまる数を求めなさい。

答え

124

解き方

48 の約数の和は、
1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 + 48 = 124

問４

1 から 99 の整数のなかで、5 で割り切れるが 4 で割り切れないものはいくつありますか。

答え

15 個

解き方

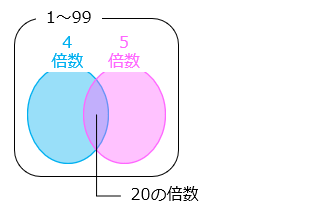
5 で割り切れるが 4 で割り切れないものは、5 の倍数から 5 と 4 の最小公倍数である 20 の倍数を除いたもの
5 で割り切れる数は、99 ÷ 5 = 19 … 4 より 19 個
20 で割り切れる数は、99 ÷ 20 = 4 … 19 より 4 個
よって、19 – 4 = 15 [個]

問５

1 より小さい分数のうち、分母が 18 で、これ以上約分できない分数はいくつありますか。

答え

6 個

解き方

18 を素因数分解すると、
18 = 2 × 3 × 3
よって、分子は 2 と 3 の倍数を除く 18 より小さい数となる。
1, 5, 7, 11, 13, 17 ⇒ 6 個

問６

素数とはどのような数ですか。簡単に説明しなさい。

答え

1 とその数自身しか約数がない数

問７

20 以下の整数で約数が 4 個である数をすべて答えなさい。

答え

6, 8, 10, 14, 15

解き方

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
約数が 1 個の 1 と約数が 2 個の素数を除くと、
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20
同じ 2 数の積となる数は約数が奇数個となるので除くと、
6, 8, 10, 12, 14, 15, 18, 20
それぞれの約数は、
6 → 1, 2, 3, 6 ⇒ 4 個
8 → 1, 2, 4, 8 ⇒ 4 個
10 → 1, 2, 5, 10 ⇒ 4 個
12 → 1, 2, 3, 6 … ⇒ 4 個以上
14 → 1, 2, 7, 14 ⇒ 4 個
15 → 1, 3, 5, 15 ⇒ 4 個
18 → 1, 2, 3, 6 … ⇒ 4 個以上
20 → 1, 2, 4, 5 … ⇒ 4 個以上

問８

1 以上の整数で、最大公約数が 5 、和が 40 となる 2 つの整数の組み合わせは 2 つあります。それぞれの組み合わせを答えなさい。

答え

5 と 35、15 と 25

解き方

最大公約数が 5 より、求める 2 つの整数はそれぞれ 5 × □、5 × ○ と表すことができる。ただし、□と○は 1 以上の整数で、同じ数ではない。
2 つの整数の和は、5 × □ + 5 × ○ = 5 × ( □ + ○ ) と表すことができる。
40 = 5 × 8 より、□ + ○ が 8 となる組み合わせを考えると、
( □, ○ ) = ( 1, 7 ) のとき、求める 2 つの整数は 5 と 35
( □, ○ ) = ( 2, 6 ) のとき、求める 2 つの整数は 10 と 30 → 最大公約数が 5 ではないので×
( □, ○ ) = ( 3, 5 ) のとき、求める 2 つの整数は 15 と 25

問９

54 をある整数で割ったところ、余りが 12 になりました。この整数として考えられるもののうち、最も小さい整数はいくつですか。

答え

14

解き方

求める整数は、54 – 12 = 42 の約数のなかで 12 より大きく最も小さい整数
42 の約数は 1, 2, 3, 6, 7, 14, 21, 42 より、14

問１０

□に当てはまる数を求めなさい。

504 × ○ = □ × □

ただし、○はできるだけ小さい整数で、□には同じ数が入ります。

答え

84

解き方

504 を素因数分解すると、
504 = 2 × 2 × 2 × 3 × 3 × 7
= ( 2 × 2 × 3 × 7 ) × ( 2 × 3 )
よって、
504 × ○ = ( 2 × 2 × 3 × 7 ) × ( 2 × 3 × 2 × 7 )
○ = 14
□ = 2 × 2 × 3 × 7 = 84

問１１

縦たてが 4 cm、横が 5 cm、高さが 6 cm の直方体があります。この直方体を、縦にも横にもすき間なく並べ、さらに上にも積み重ねてできる立方体のうち、最も小さいものを作ります。このとき、もとの直方体は何個必要ですか。

答え

1800 個

解き方

立方体の 1 辺の長さは、直方体の縦、横、高さの長さの最小公倍数である 60 cm になる。必要な直方体の個数は、
縦：60 ÷ 4 = 15 [個]
横：60 ÷ 5 = 12 [個]
高さ：60 ÷ 6 = 10 [個]
よって、15 × 12 × 10 = 1800 [個]

問１２

整数 A の約数の和を記号【 A 】で表すことにします。

例えば、【 4 】= 1 + 2 + 4 = 7、【 6 】= 1 + 2 + 3 + 6 = 12 となります。

A を 10 から 30 までの整数としたとき、【 A 】- A = 1 となるような A は全部で何個ありますか。

答え

6 個

解き方

この問題文の条件の A は素数である。よって、11, 13, 17, 19, 23, 29 の 6 個