算数【基本】図形の移動
問1
(1)図のように、直角をはさむ辺が 8 cm である直角二等辺三角形 ABC が直線上に固定されています。同じ直線上を、1 辺 4 cm の正方形が毎秒 1 cm の速さで直線に沿って矢印の方向に進みます。はじめ、直角二等辺三角形の頂点 A と正方形の頂点 P は、図のように 5 cm 離れています。
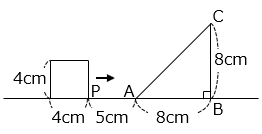
① 正方形が移動を始めてから 5 秒後までは、2 つの図形が重なってできる図形の面積は 0 cm2 です。正方形がさらに移動を続けて、重なってできる図形の面積がふたたび 0 cm2 となるのは、正方形が移動を始めてから何秒後ですか。
- 答え(1)- ①
- 17 秒後
- 解説(1)- ①
- 図のように P 以外の正方形の各頂点を Q、R、S とする。重なってできる図形の面積がふたたび 0 cm2となるのは、Q と B が重なるときである。
QがBに移動する距離は
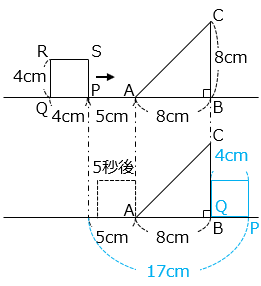
5 + 8 + 4 = 17 [cm]
よって、17 [秒後]
② 正方形が移動を始めてから 7 秒後、2 つの図形が重なってできる図形は直角二等辺三角形です。このとき、重なってできる図形の面積を答えなさい。
- 答え(1)- ②
- 2 cm2
- 解説(1)- ②
- 7 秒後、P は元の位置から 1 × 7 = 7 [cm] 移動している。
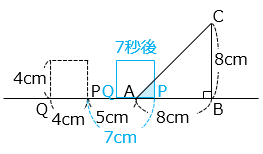
よって、求める面積は 2 × 2 ÷ 2 = 2 [cm2]
③ 正方形が移動を始めてから 11 秒後、2 つの図形が重なってできる図形の名称と面積を答えなさい。
- 答え(1)- ③
- 名称:五角形 面積:14 cm2
- 解説(1)- ③
- 11 秒後、P は元の位置から 11 cm 移動している。
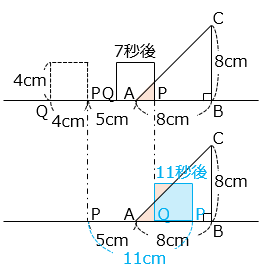
重なってできる図形は五角形。
求める面積は 4 × 4 – 2 = 14 [cm2]
④ 2 つの図形が重なってできる図形が正方形になるのは何秒後ですか。また、重なってできた正方形の面積を答えなさい。
- 答え(1)- ④
- 13 秒後、16 cm2
- 解説(1)- ④
- 重なってできる図形が正方形になるのは、P が B と重なるとき。
P が B と重なるのは
5 + 8 = 13 [秒] 進んだとき
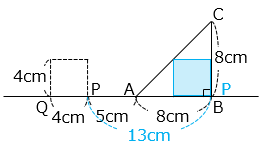
面積は 4 × 4 = 16 [cm2]
⑤ 正方形が移動を始めてから 16 秒後、2 つの図形が重なってできる図形の名称と面積を答えなさい。
- 答え(1)- ⑤
- 名称:長方形 面積:4 cm2
- 解説(1)- ⑤
- 16 秒後、P は元の位置から 16 cm 移動している。
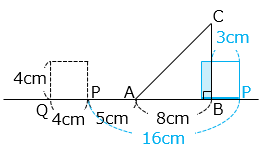
重なってできる図形は長方形。
求める面積は 1 × 4 = 4 [cm2]
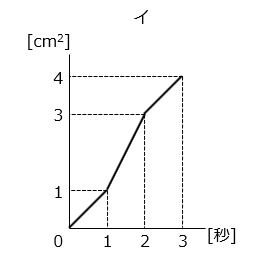
(2)図 1 のような長方形の厚紙と、図 2 のように 1 辺 1 cm の正方形を並べた厚紙があります。図 3 のように、図 2 の厚紙を長方形の辺 AD にそって矢印の向きに毎秒 1 cm の速さで移動させます。頂点 P を点 D から A まで移動させるとき、時間と重なった部分の面積の関係を表すグラフとして正しいものを、ア~カの中から 1 つ選びなさい。
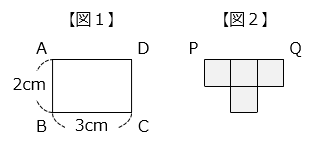

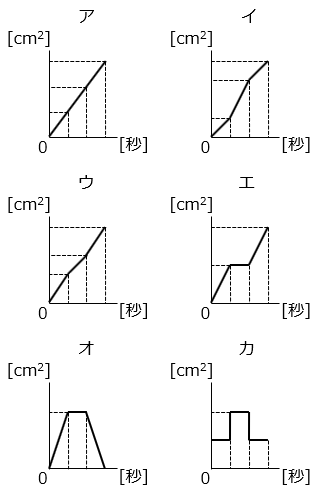
- 答え(2)
- イ
- 解説(2)
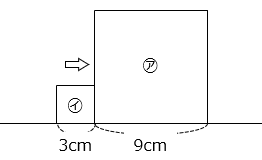
(3)図のような正方形㋐と㋑があります。㋐を固定して㋑を一定の速さで図の位置から矢印の方向に動かします。グラフは、㋑が動き始めてからの時間と、㋑と重なっていない㋐の部分の面積の関係を表しています。
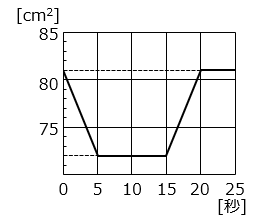
① ㋑の速さは秒速何 cm ですか。
- 答え(3)- ①
- 秒速 0.6 cm
- 解説(3)- ①
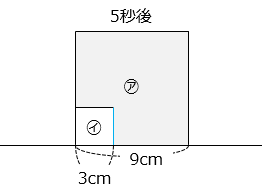
5秒後は㋑全体が㋐の中に入ったときなので、
3 ÷ 5 = 0.6 [cm/秒]
② ㋑が動き始めてから 17 秒後の㋑と重なっていない㋐の面積は何 cm2 ですか。
- 答え(3)- ②
- 75.6 cm2
- 解説(3)- ②
- 17 秒後、㋑は 0.6 × 17 = 10.2 [cm] 移動している。
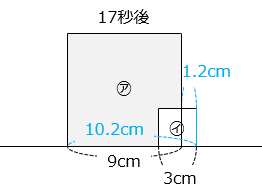
㋐と㋑が重なっている部分の面積は、
3 × ( 3 – 1.2 ) = 5.4 [cm2]
よって求める面積は、
81 – 5.4 = 75.6 [cm2]
(4)図のように、直線状に正方形 ABCD と台形 PQRS が 2 cm はなれて置かれています。正方形 ABCD は、この位置から右へ毎秒 1cm の速さで直線状を動き、点 A が点 Q に重なると止まります。
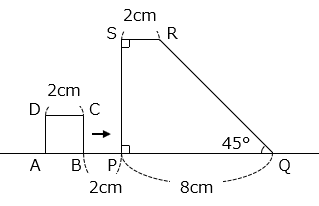
① 正方形 ABCD が動いているのは何秒間ですか。
- 答え(4)- ①
- 12 秒間
- 解説(4)- ①
点 A が動いた距離は 12 cm より、
12 ÷ 1 = 12 [秒間]
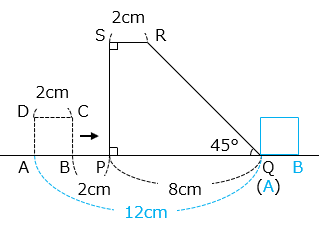
② 2 つの図形が重なる部分の面積が 4 cm2 になるのは何秒間ですか。
- 答え(4)- ②
- 4 秒間
- 解説(4)- ②
- 2 つの図形が重なる部分の面積が 4 cm2 になるのは、正方形 ABCD が完全に台形 PQRS の中にあるとき。すなわち、点 A が点 P に重なってから、点 C が辺 QR と接するまでの間となる。
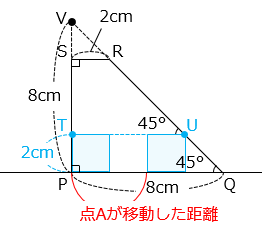
図のように、点 A が点 P と重なったときの点 D の位置を T、点 C が辺 QR と接した位置を U、 辺 PS と辺 QR の延長上の交点を V とする。
VT = TU = 6 [cm]
点 A が点 P に重なってから、点 C が辺 QR と接するまでに点 A が移動した距離は 6 – 2 = 4 [cm]
よって、求める時間は 4 秒間。
③ 2 つの図形が重なる部分の面積が 2 cm2 になるのは、正方形 ABCD が動き始めてから何秒後と何秒後ですか。
- 答え(4)- ③
- 3 秒後と 10 秒後
- 解説(4)- ③
- 2 つの図形が重なる部分の面積が 2 cm2 になるのは、図のように、【1】点 P が辺 AB の中点になったときと、【2】正方形 ABCD の対角線 BD が辺 QR と重なったとき、すなわち点 B が点 Q と重なったときとなる。
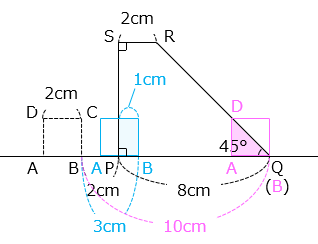
【1】点 B が移動した距離は 3 cm より、3 秒後
【2】点 B が移動した距離は 10 cm より、10 秒後
問2
(1)図は、点 O を中心として半径 10 cm の円が平面上を滑ることなく矢印の方向に 1 回転させて移動させたものです。このとき、点 O が移動した距離(図の太線部分の長さ)は何 cm ですか。ただし、円周率を 3.14 とします。
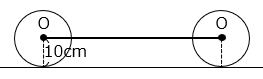
- 答え(1)
- 62.8 cm
- 解説(1)
- 求める距離は円周に等しい。
10 × 2 × 3.14 = 62.8 [cm]
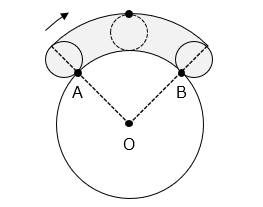
(2)図 1 は半径が 4 cm の 2 つのおうぎ形を組み合わせたものです。また、図 2 の太線は、半径 2 cm の円を図 1 の周囲に沿ってすべることなく回転させながら動かしたとき、円の中心 O が移動したあとを途中まで表したものです。
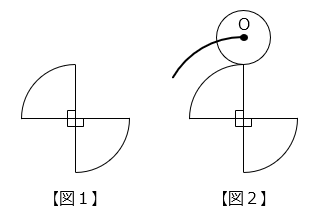
① 円は図 1 を 1 周し、元も場所に戻るものとします。このとき、中心 O が移動したあと(図 2 の太線の続き)をかきなさい。
- 答え(2)- ①
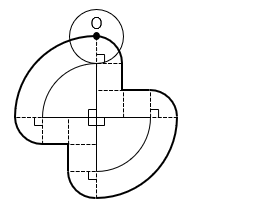
② ①でかいた線の長さの和は何 cm ですか。ただし、すでに図にかかれている線も含めます。また、円周率は 3.14 とします。
- 答え(2)- ②
- 39.4 cm
- 解説(2)- ②

6 × 2 × 3.14 × \(\dfrac{90\ ×\ 2}{360}\) + 2 × 2 × 3.14 × \(\dfrac{90\ ×\ 4}{360}\) + 2 × 4
= ( 6 + 4 ) × 3.14 + 8 = 39.4 [cm]
(3)半径 2 cm、中心角 90°のおうぎ形 OAB があります。このおうぎ形を、線分 OA が直線に重なった位置から、線分 OB が直線に初めて重なるまで、矢印の方向に直線上をすべらないように回転させます。以下の問いに答えなさい。ただし、円周率は 3.14 とします。
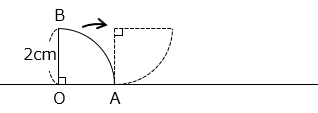
① 点 O が動いてできる線の長さを求めなさい。
- 答え(3)- ①
- 9.42 cm
- 解説(3)- ①
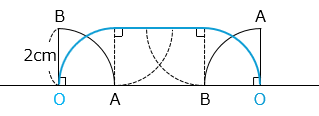
点 O が動いた線を青線で表した。
2 × 2 × 3.14 × \(\dfrac{90\ ×\ 2}{360}\) + 2 × 2 × 3.14 × \(\dfrac{90}{360}\)
= 2 × 3.14 + 3.14 = 9.42 [cm]
② 点 O が動いてできる線と直線で囲まれた部分の面積を求めなさい。
- 答え(3)- ②
- 12.56 cm2
- 解説(3)- ②
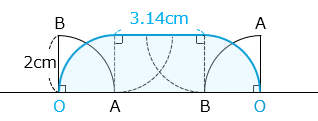
点 O が動いた線を青線で表した。
2 × 2 × 3.14 × \(\dfrac{90\ ×\ 2}{360}\) + 2 × 3.14
= 2 × 3.14 + 2 × 3.14 = 12.56 [cm2]
(4)図のように、正三角形 ABC が長方形の辺上をすべらないように、もとの位置に戻るまで回転しながら動きます。このとき、点 A の動いた道のりは何 cm ですか。以下の問いに答えなさい。ただし、円周率は 3.14 とします。
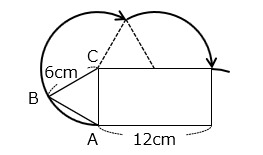
- 答え(4)
- 69.08 cm
- 解説(4)
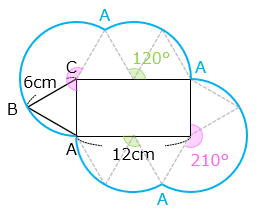
点 A が動いた線を青線で表した。
{ 6 × 2 × 3.14 × \(\dfrac{210}{360}\) + 6 × 2 × 3.14 × \(\dfrac{120}{360}\) } × 2
= ( 7 × 3.14 + 4 × 3.14 ) × 2
= ( 11 × 3.14 ) × 2 = 69.08 [cm]
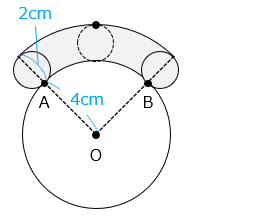
(5)半径 4 cm の大円 O と半径 1 cm の小円があり、小円の周上には 1 か所●印がついています。図のように、A の位置でその●印は大円 O の周上にあります。この位置から小円を大円にそってすべらないように回転させ、次に●印が大円 O の周上にくるのが B の位置です。ただし、円周率は 3.14 とします。
① 大円 O の一部である A から B までの長さは何 cm ですか。
- 答え(5)- ①
- 6.28 cm
- 解説(5)- ①
- A から B までの長さは、小円の円周の長さに等しいので、
1 × 2 × 3.14 = 6.28 [cm]
② おうぎ形 OAB の面積は何 cm2 ですか。
- 答え(5)- ②
- 12.56 cm2
- 解説(5)- ②
- 小円の半径は大円の半径の \(\dfrac{1}{4}\) より、小円の円周は大円の円周の \(\dfrac{1}{4}\) である。よって、
4 × 4 × 3.14 × \(\dfrac{1}{4}\) = 12.56 [cm2]
③ 図の 部分の面積は何 cm2 ですか。
- 答え(5)- ③
- 18.84 cm2
- 解説(5)- ③
1 × 1 × 3.14 + 6 × 6 × 3.14 × \(\dfrac{1}{4}\) – 12.56
= ( 1 + 9 ) × 3.14 -12.56 = 18.84 [cm2]
(6)図のような辺の長さが 8 cm、6 cm、10 cm の三角形があります。この三角形の外側を半径 2 cm の円が辺から離れることなく 1 周するとき、円が通ったあとの面積を求めなさい。ただし、円周率は 3.14 とします。
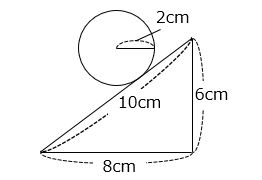
- 答え(6)
- 146.24 cm2
- 解説(6)
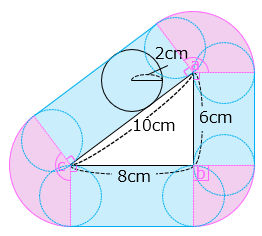
求める面積は 3 つの長方形 ( ■ ) と 3 つのおうぎ形 ( ■ ) の面積の和となる。また、このとき 3 つのおうぎ形の中心角の和 ( a + b + c ) は 360°である。
4 × 8 + 4 × 6 + 4 × 10 + 4 × 4 × 3.14
= 4 × ( 8 + 6 + 10 + 12.56 )
= 4 × 36.56 = 146.24 [cm2]
(7)縦 30 cm、横 50 cm の長方形があります。この長方形の内部を半径 5 cm の円が長方形の辺にそって 1 周します。以下の問いに答えなさい。ただし、円周率は 3.14 とします。
① 円の中心が移動する長さは何 cm ですか。
- 答え(7)- ①
- 120 cm
- 解説(7)- ①
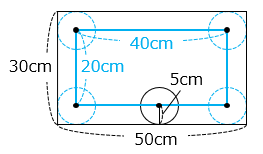
円の中心が描く図形は、縦 30 – 5 × 2 = 20 [cm]、横 50 – 5 × 2 = 40 [cm] の長方形より、
20 × 2 + 40 × 2 = 120 [cm]
② 円が通り過ぎる部分の面積は何 cm2 ですか。
- 答え(7)- ②
- 1178.5 cm2
- 解説(7)- ②
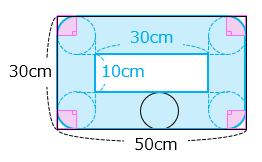
求める面積は、外側の長方形から、内側の長方形と 4 つの正方形 ( □ ) を除き、4 つのおうぎ形 ( ■ ) を足した面積になる。
30 × 50 – 10 × 30 – 5 × 5 × 4 + 5 × 5 × 3.14 × \(\dfrac{1}{4}\) × 4
= 1500 – 300 – 100 + 25 × 3.14
= 1100 + 78.5 = 1178.5 [cm2]
(8)図は直角三角形 ABC を点 C を中心に 120 度回転させ、三角形 A’B’C の位置に移動したことを表しています。 部分の面積を求めなさい。ただし、円周率は 3.14 とします。
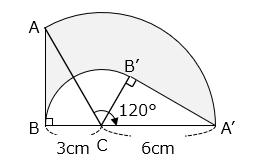
- 答え(8)
- 28.26 cm2
- 解説(8)
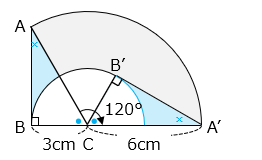
■部分の面積は等しいことから、求める面積は、
6 × 6 × 3.14 × \(\dfrac{120}{360}\) – 3 × 3 × 3.14 × \(\dfrac{120}{360}\)
= ( 12 – 3 ) × 3.14 = 28.26 [cm2]
(9)図のような長方形 ABCD があります。この長方形を直線上をすべらないように転がしていきます。再び辺 AB が直線上に来たところで転がすのをやめます。このとき、点 C が動いた距離は何 cm ですか。ただし、円周率は 3.14 とします。
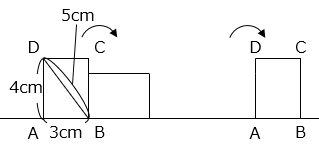
- 答え(9)
- 18.84 cm
- 解説(9)
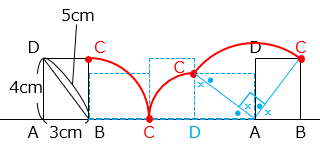
C の動きを赤線で示した。
C の動いた距離は、4 × 2 × 3.14 × \(\dfrac{90}{360}\) + 3 × 2 × 3.14 × \(\dfrac{90}{360}\) + 5 × 2 × 3.14 × \(\dfrac{90}{360}\)
= ( 8 + 6 + 10 ) × \(\dfrac{1}{4}\) × 3.14
= 6 × 3.14 = 18.84 [cm]






































