算数【応用】図形の移動
円周率は 3.14 とします。
問1
半径 2 cm の円を 1 辺 16 cm の正方形の内側に沿って転がします。
(1)図の A の位置から B の位置まで円を転がしたとき、円が通過した 部分の面積は何 cm2 ですか。
- 答え(1)
- 60.56 cm2
- 解き方(1)
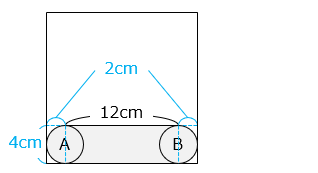
求める面積は、半径 2 cm の円の面積と、縦 4 cm、横 12 cm の長方形の面積の和となる。
2 × 2 × 3.14 + 4 × 12
= 12.56 + 48 = 60.56 [cm2]
(2)図の A の位置から円を正方形の内側に沿って 1 周転がしたとき、円が通過した部分の面積は何 cm2 ですか。
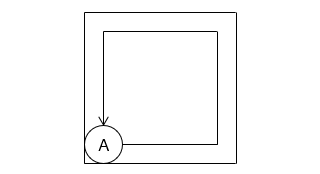
- 答え(2)
- 188.56 cm2
- 解き方(2)
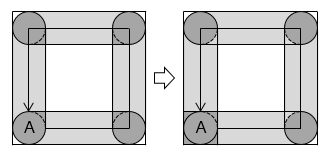
求める面積の図形は、(1)の 部分の図形を 4 つ組み合わせた形をしており、 部分が重なっている。
重なった部分の面積は、
2 × 2 × 3.14 × 3 + 4 × 4
= 4 × ( 3.14 × 3 + 4 )
= 4 × ( 9.42 + 4 )
= 4 × 13.42 = 53.68 [cm2]
よって、求める面積は、
60.56 × 4 – 53.68 = 188.56 [cm2]
(3)図のように 1 辺 16 cm の正方形から 1 辺 4 cm の正方形を 4 つ切り取ります。このとき、円を図形の内側に沿って 1 周転がしたとき、円が通過した部分の面積は何 cm2 ですか。
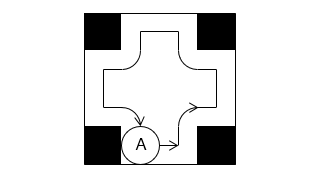
- 答え(3)
- 171.36 cm2
- 解き方(3)
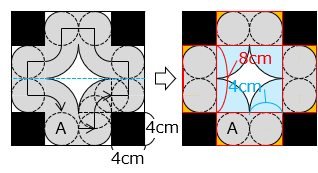
求める面積は、 部分。
部分の面積は、半径 4 cm の円 ( ) と、赤線の長方形 4 個から 部分の面積を除いたものとなる。
部分の面積は、1 個の赤線の長方形から半径 2 cm の円を 2 個除いた面積より、
4 × 8 – 2 × 2 × 3.14 × 2
= 8 × ( 4 – 3.14 )
= 8 × 0.86 = 6.88 [cm2]
求める面積は、
4 × 4 × 3.14 + 4 × 8 × 4 – 6.88
= 50.24 + 128 – 6.88 = 171.36 [cm2]
問2
図のように、半径 8 cm、中心角 45° のおうぎ形が地面にそって、(ア)の位置から(イ)の位置へすべることなく 1 回転して移動します。
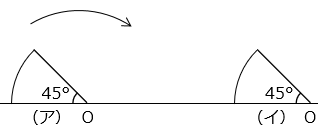
(1)(ア)と(イ)の点 O の位置は、何 cm はなれていますか。
- 答え(1)
- 22.28 cm
- 解き方(1)
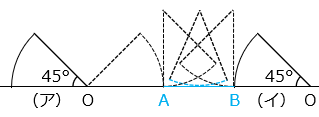
AB 間の長さはおうぎ形の弧の長さに等しい。
(ア)と(イ)の点 O の位置は、
8 + 8 × 2 × 3.14 × \(\dfrac{45}{360}\) + 8
= 8 + 6.28 + 8 = 22.28 [cm]
はなれている。
(2)点 O が通ったあとの長さを求めなさい。
- 答え(2)
- 31.4 cm
- 解き方(2)

点 O が通ったあとを青線で示した。
図よりその長さは、
8 × 2 × 3.14 × \(\dfrac{90}{360}\) × 2 + 6.28
= 25.12 + 6.28 = 31.4 [cm]
問3
図のような長方形 ABCD があります。点 O を中心として、三角形 OAB を点 A が点 B、C、D を通るように 360° 回転させたとき、辺 AB が通過する部分の面積を求めなさい。
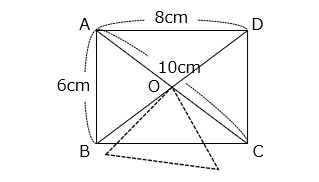
- 答え
- 28.26 cm2
- 解き方
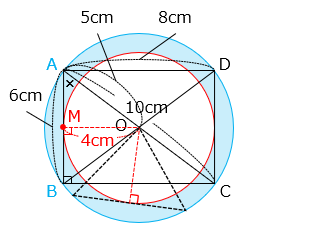
点 A、B は青線上を移動する。辺 AB の中点を M とすると、点 M は赤線上を移動する。したがって、辺 AB が通過するのは 部分となる。
△OAM と △CAB は相似の関係にあり、相似比は OA:CA = 1:2 である。よって、OM = CB × \(\dfrac{1}{2}\) = 8 × \(\dfrac{1}{2}\) = 4 [cm]
よって、求める面積は、
5 × 5 × 3.14 – 4 × 4 × 3.14
= ( 25 – 16 ) × 3.14
= 9 × 3.14 = 28.26 [cm2]
問4
図の長方形をすべらないように矢印の向きに 1 回転させたとき、点 P が描く図形の長さを求めなさい。

- 答え
- 18.84 cm
- 解き方
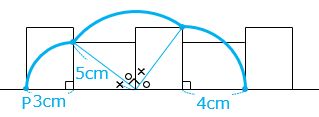
点 P が描く図形を太い青線で示した。
図よりその長さは、
3 × 2 × 3.14 × \(\dfrac{90}{360}\) + 5 × 2 × 3.14 × \(\dfrac{90}{360}\) + 4 × 2 × 3.14 × \(\dfrac{90}{360}\)
= 2 × 3.14 × \(\dfrac{90}{360}\) × ( 3 + 5 + 4 )
= 2 × 3.14 × \(\dfrac{1}{4}\) × 12
= 3.14 × 6 = 18.84 [cm]
問5
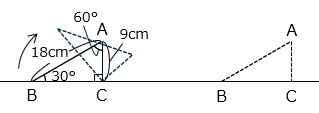
図のように、直線状に直角三角形 ABC があります。この直角三角形 ABC を、直線状をすべらないように矢印の方向に一回転させました。このとき、頂点 A が描く曲線の長さを求めなさい。
- 答え
- 61.23 cm
- 解き方

頂点 A が描く曲線を太い青線で示した。
図よりその長さは、
9 × 2 × 3.14 × \(\dfrac{90}{360}\) + 18 × 2 × 3.14 × \(\dfrac{150}{360}\)
= 9 × 2 × 3.14 × \(\dfrac{1}{4}\) + 18 × 2 × 3.14 × \(\dfrac{5}{12}\)
= 4.5 × 3.14 + 15 × 3.14
= 19.5 × 3.14 = 61.23 [cm]
問6
図の直方体 ABCD-EFGH を、辺 FG が床と離れず、すべらないように面 BFGC が床につくまで倒しました。
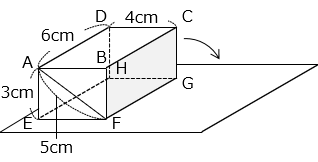
(1)点 A が動いた長さは何 cm ですか。
- 答え(1)
- 7.85 cm
- 解き方(1)
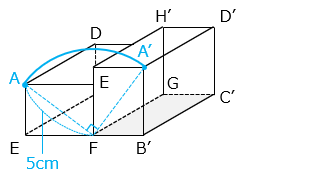
点 A が描く曲線を太い青線で示した。
図よりその長さは、
5 × 2 × 3.14 × \(\dfrac{90}{360}\)
= 10 × 3.14 × \(\dfrac{1}{4}\)
= 2.5 × 3.14 = 7.85 [cm]
(2)四角形 AEFB が動いた部分の面積は何 cm2 ですか。
- 答え(2)
- 31.625 cm2
- 解き方(2)
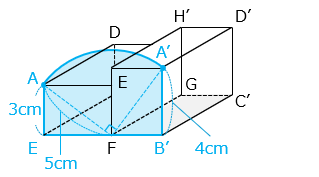
四角形 AEFB が動いた部分の面積を で示した。
図よりその面積は、
5 × 5 × 3.14 × \(\dfrac{90}{360}\) + 3 × 4 × \(\dfrac{1}{2}\) × 2
= 6.25 × 3.14 + 12
= 19.625 + 12 = 31.625 [cm2]
(3)直方体 ABCD-EFGH が動いた部分の体積は何 cm3 ですか。
- 答え(3)
- 189.75 cm3
- 解き方(3)

直方体 ABCD-EFGH が動いた部分の体積は、四角形 AEFB が動いた部分の面積 を底面とした高さ 6 cm の立体の体積となる。
よって求める体積は、
31.625 × 6 = 189.75 [cm3]
問7
1 辺の長さが 3 cm の正六角形が 2 つつながった図形があります。この図形のまわりを 1 辺 3 cm の正三角形 ABC が【図1】から【図2】の位置まで矢印の方向にすべることなく回転します。
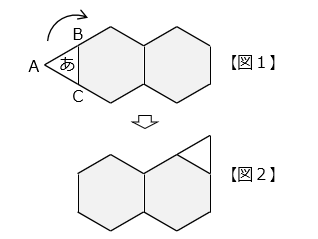
(1)正三角形が【図2】の位置にきたとき、あてはまるものをア~カから選びなさい。

- 答え(1)
- ウ
- 解き方(1)

図より、ウ
(2)頂点 A が動いた長さは何 cm ですか。
- 答え(2)
- 21.98 cm
- 解き方(2)

頂点 A が描く曲線を太い青線で示した。
図よりその長さは、
3 × 2 × 3.14 × \(\dfrac{180}{360}\) × 2 + 3 × 2 × 3.14 × \(\dfrac{60}{360}\)
= 6 × 3.14 + 3.14
= 7 × 3.14 = 21.98 [cm]
問8
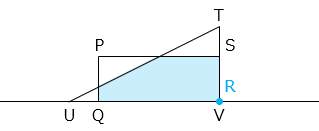
図のように、直線上に長方形 A と直角三角形 B があります。長方形 A は図の位置から矢印の方向に秒速 1 cm で動きます。
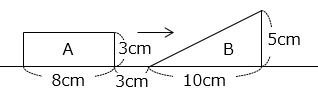
(1)A と B が重なり始めてから重なり終わるまでにかかる時間を求めなさい。
- 答え(1)
- 18 秒
- 解き方(1)

図のように、長方形 A の各頂点を P、Q、R、S とし、直角三角形 B の各頂点を T、U、V とする。
A と B が重なり始めるのは R が U の位置に来たとき、A と B が重なり終わるのは Q が V の位置に来たときとなる。
この間に A が移動した距離を青矢印で示した。その距離は 8 + 10 = 18 [cm] より、かかった時間は、
18 ÷ 1 = 18 [秒]
(2)動き始めてから 5 秒後の、A と B が重なる部分の面積は何 cm2 ですか。
- 答え(2)
- 1 cm2
- 解き方(2)
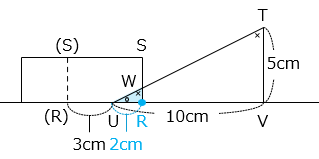
動き始めてから 5 秒後、 A が移動した距離は 1 × 5 = 5 [cm] より、R は U より右に 2 cm の位置にある。A の辺 RS と B の辺 TU の交点を W とすると、重なった部分は △WUR ( ) である。
△WUR と △TUV は相似 ( 2 つの角の大きさが等しい ) で、相似比は UR:UV = 2:10 = 1:5、面積比は △WUR:△TUV = 1:25 より、
△WUR = △TUV × \(\dfrac{1}{25}\)
= 10 × 5 × \(\dfrac{1}{2}\) × \(\dfrac{1}{25}\)
= 25 × \(\dfrac{1}{25}\) = 1 [cm2]
(3)動き始めてから 15 秒後の、A と B が重なる部分の面積は何 cm2 ですか。
- 答え(3)
- 17 cm2
- 解き方(3)

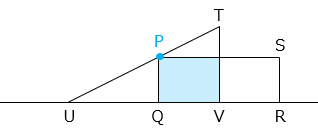
動き始めてから 15 秒後、 A が移動した距離は 1 × 15 = 15 [cm] より、R は V より右に 2 cm、Q は U より右に 4 cm の位置にある。A の辺 PQ、PS と B の辺 TU の交点をそれぞれ X、Y とし、A の辺 PS と B の辺 TV の交点を Z とする。
重なった 部分の面積は、△TUV から △XUQ と △TYZ の面積を除くことで求めることができる。
△XUQ と △TUV は相似で、相似比は UQ:UV = 4:10 = 2:5、面積比は △XUQ:△TUV = 4:25 より、
△XUQ = △TUV × \(\dfrac{4}{25}\)
= 25 × \(\dfrac{4}{25}\) = 4 [cm2]
また、△XUQ と △TYZ は合同 ( 1 辺の長さとその両端の角の大きさが等しい ) なので、面積は等しい。よって、求める面積は、
25 – 4 × 2 = 17 [cm2]
(4)A と B が重なる部分の図形は時間が経つにつれて変化していきます。どのような形に変化していくのか、変化する順に答えなさい。ただし、下のア~カから選んで答えなさい。
ア. 長方形
イ. 台形
ウ. 直角三角形
エ. 二等辺三角形
オ. 正三角形
カ. 五角形
- 答え(4)
- ウ → イ → カ → ア
- 解き方(4)
- R が U に到達してから S が辺 TU 上に到達するまで ⇒ 直角三角形
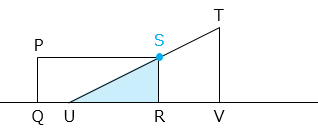
S が辺 TU 上に到達してから Q が U に到達するまで ⇒ 台形
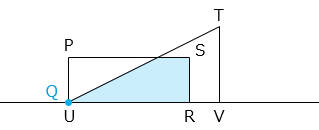
Q が U に到達してから R が V に到達するまで ⇒ 五角形
R が V に到達してから Q が V に到達するまで ⇒ 長方形
問9
【図 1】のように、1 辺の長さが 4 cm の正三角形から、半径が 2 cm のおうぎ形を 3 個切り取ってできた図形 P があります。この図形 P を、【図 2 】のように半径が 2 cm の円 O の周上にぴったりと重ね、すべらないように矢印の方向に円 O の周上を転がします。1 辺の長さが 4 cm の正三角形の面積は 6.93 cm2 とします。
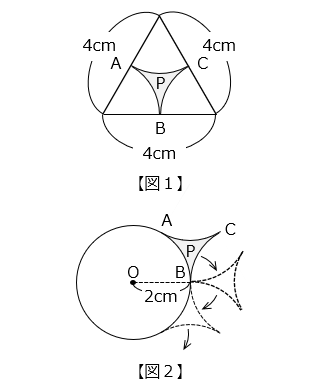
(1)図形 P の面積は何 cm2 ですか。
- 答え(1)
- 0.65 cm2
- 解き方(1)
- 図形 P の面積は、1 辺の長さが 4 cm の正三角形の面積から半径が 2 cm で中心角が 60° のおうぎ形 3 個分の面積を除いたものより、
6.93 – 2 × 2 × 3.14 × \(\dfrac{60\ ×\ 3}{360}\)
= 6.93 – 4 × 3.14 × \(\dfrac{1}{2}\)
= 6.93 – 2 × 3.14
= 6.93 – 6.28 = 0.65 [cm2]
(2)図形 P がはじめてもとの位置にもどるまで転がったとき、点 A が動いたあとの線の長さは何 cm ですか。
- 答え(2)
- 25.12 cm
- 解き方(2)
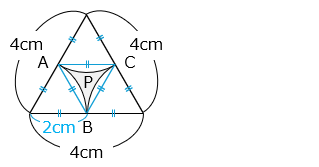

点 A が動いたあとの線を太い青線で示した。図形 P が 1 回転がるごとに 180° 回転する。よって、
2 × 2 × 3.14 × \(\dfrac{180\ ×\ 4}{360}\)
= 2 × 2 × 3.14 × 2 = 25.12 [cm]
(3)図形 P がはじめてもとの位置にもどるまで転がったとき、点 A が動いた部分の面積は何 cm2 ですか。
- 答え(3)
- 38.98 cm2
- 解き方(3)

図より、求める面積 ( ) は、半円 4 つと 1 辺の長さが 4 cm の正三角形 2 つの和となる。
よって、
2 × 2 × 3.14 × 2 + 6.93 × 2
= 25.12 + 13.86 = 38.98 [cm2]



































