算数【基本】図形上の点の移動
問1
(1)図のような直角三角形があり、点 P が B → C → A の順に毎秒 2 cm の速さで三角形の辺上を動いています。
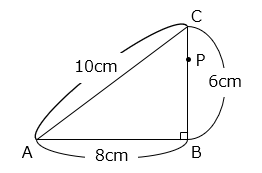
① 点 P が B を出発して A に到達するまでにかかる時間は何秒ですか。
- 答え(1)- ①
- 8 秒
- 解き方(1)- ①
- B からA (B → C → A) までの長さは 6 + 10 = 16 [cm]、点 P の速さは毎秒 2 cm より、
16 ÷ 2 = 8 [秒]
② 2 秒後の三角形 PABの面積は何 cm2 ですか。
- 答え(1)- ②
- 16 cm2
- 解き方(1)- ②
- 2 秒後の点 P は、B から 2 × 2 = 4 [cm] の位置にある。
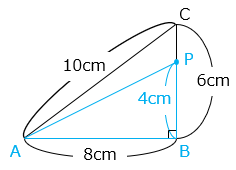
よって、△PAB の面積は、
8 × 4 ÷ 2 = 16 [cm2]
③ 5 秒後の三角形 PABの面積は何 cm2 ですか。
- 答え(1)- ③
- 14.4 cm2 ( または、\(14\dfrac{2}{5}\) cm2 )
- 解き方(1)- ③
- 5 秒後の点Pは、B から 2 × 5 = 10 [cm] の位置にある。すなわち、辺 AC 上の C から 4 cm の位置にある。
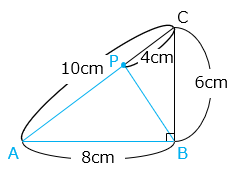
AP:AC = 6:10 = 3:5 より、△PAB:△CAB = 3:5 より、
△PAB = △CAB × \(\dfrac{3}{5}\)
= ( 8 × 6 ÷ 2 ) × \(\dfrac{3}{5}\)
= 24 × \(\dfrac{3}{5}\) = 14.4 [cm2]
(2)図のような、縦 60 cm、横 80 cm の長方形 ABCD において、点 E と点 F はそれぞれ辺 AB、辺 DC の真ん中の点です。点 P は辺 AD 上を A から D に向かって毎秒 4 cm の速さで動きます。点 Q は辺 EF 上を F から E に向かって毎秒 2 cm の速さで動きます。点 R は辺 BC 上を B から C に向かって毎秒 1 cm の速さで動きます。3 点 P、Q、R は同時に出発します。
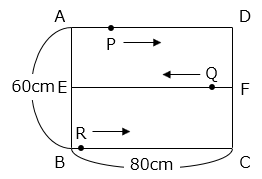
① 点 P、Q、R が出発してから 15 秒後の三角形 EQR の面積は何 cm2 ですか。
- 答え(2)- ①
- 750 cm2
- 解き方(2)- ①
- 15 秒後の点 Q は、F から 2 × 15 = 30 [cm] の位置にある。15 秒後の点 R は、B から 1 × 15 = 15 [cm] の位置にある。
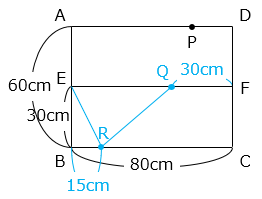
△EQR は底辺 EQ、高さ EB の三角形であることから、
△EQR
= 50 × 30 ÷ 2 = 750 [cm2]
② 三角形 AEP の面積が四角形 AEFD の面積の \(\dfrac{1}{4}\) になるのは、点 P が A を出発してから何秒後ですか。
- 答え(2)- ②
- 10 秒後
- 解き方(2)- ②
- △AEP の面積が□AEFD の面積の \(\dfrac{1}{4}\) になるのは、点 P が辺 AD の真ん中に達したときである。
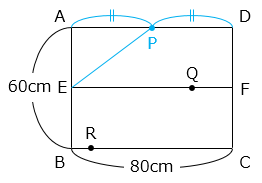
よって、
40 ÷ 4 = 10 [秒後]
(3)1 辺が 10 cm の正方形 ABCD があります。点 P は頂点 A から頂点 B を通って頂点 C まで、辺 AB、辺 BC 上を毎秒 2 cm の速さで移動します。点 Q は頂点 D から頂点 C まで、辺 DC 上を毎秒 1 cm の速さで移動します。点 P と点 Q は同時に動き出します。
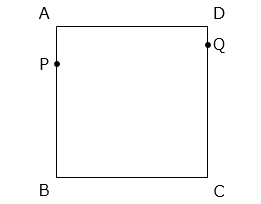
① 点 P と点 Q が同時に動き出してから、3 秒後の四角形 APQD の面積を求めなさい。
- 答え(3)- ①
- 45 cm2
- 解き方(3)- ①
- 3 秒後、点 P は辺 AB 上の A から 2 × 3 = 6 [cm] の位置にあり、点 Q は辺 DC 上の D から 1 × 3 = 3 [cm] の位置にある。
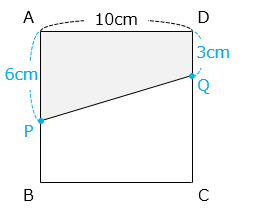
□APQD の面積は、
( 6 + 3 ) × 10 ÷ 2 = 45 [cm2]
点 P が辺 BC 上にあるとき、四角形 BPQD の面積が 46 cm2 になりました。
② 三角形 PCQ の面積を求めなさい。
- 答え(3)- ②
- 4 cm2
- 解き方(3)- ②
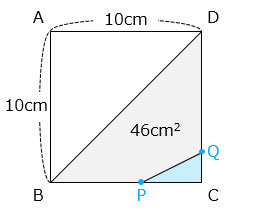
△PCQ
= △BCD – □BPQD
= 10 × 10 ÷ 2 – 46 = 4 [cm2]
③ PC:CQ を最も簡単な整数の比で表しなさい。
- 答え(3)- ③
- 2:1
- 解き方(3)- ③
- 点 P と点 Q は同時に点 C に到着するので、点 P と点 Q の速度がPC:CQの比となる。
【別解】
点 P と点 Q が動き出してから□秒後とすると、AB + BP = 2 × □ [cm]、DQ = □ [cm] と表すことができる。よって、
PC:CQ
= 20 – 2 × □:10 – □
= 2 × ( 10 – □ ):1 × ( 10 – □ )
= 2:1
④ DQ は何 cm ですか。
- 答え(3)- ④
- 8 cm
- 解き方(3)- ④
- △PCQ = 4 [cm2] より、PC × CQ = 4 × 2 = 8
また、PC:CO = 2:1 より、PC = 4 [cm]、CQ = 2 [cm] となる。
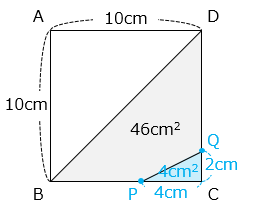
DQ = 10 – 2 = 8 [cm]
問2
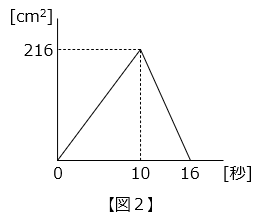
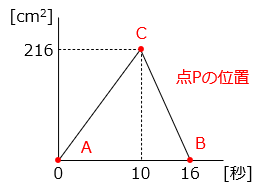
(1)図 1 のように、角 B が直角である直角三角形 ABC の辺の上を、点 P が A → C → B の順に毎秒 3 cm の速さで動きます。図 2 のグラフは、点 P が A を出発してからの時間と三角形 APB の面積の関係を表したものです。
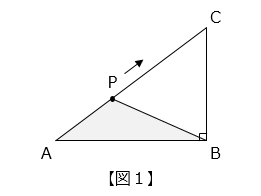
- ヒント
AC = 3 × 10 = 30 [cm]
CB = 3 × 6 = 18 [cm]
① BC の長さは何 cm ですか。
- 答え(1)- ①
- 18 cm
- 解き方(1)- ①
- グラフより、点 P は A を出発してから 10 秒後に C に達し、16 秒後に B に達したことが分かる。
よって、
BC = 3 × ( 16 – 10 ) = 18 [cm]
② 点 P が A を出発してから 14 秒後の三角形 APB の面積は何 cm2 ですか。
- 答え(1)- ②
- 72 cm2
- 解き方(1)- ②
- A を出発してから 14 秒後の点 P は、BC 上の C から、3 × 4 = 12 [cm] の位置にある。
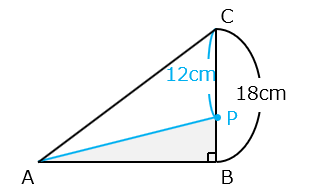
△APB:△ACB = PB:CB = 1:3
△ABC の面積は 216 cm2 なので、
△APB = 216 × \(\dfrac{1}{3}\) = 72 [cm2]
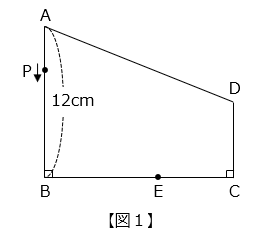
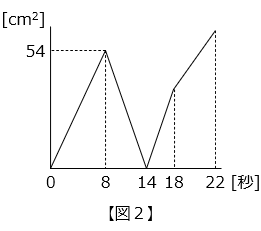
(2)図 1 のように、辺 AB の長さが 12 cm である四角形 ABCD があり、点 E を辺 BC 上にとります。点 P は四角形 ABCD の辺上を A → B → C → D の順に動きます。図 2 のグラフは、点 P が A を出発してからの時間と三角形 PAE の面積の関係を表したものです。
- ヒント
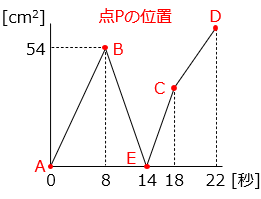
① 点 P の速さは秒速何 cm ですか。
- 答え(2)- ①
- 秒速 1.5 cm ( または、秒速 \(1\dfrac{1}{2}\) cm )
- 解き方(2)- ①
- グラフより、点 P が B に達するのにかかる時間は 8 秒なので、
12 ÷ 8 = 1.5 [cm / 秒]
② 点 P が A を出発してから、三角形 PAE の面積が 2 回目に 36 cm2 になるのは何秒後ですか。
- 答え(2)- ②
- 10 秒後
- 解き方(2)- ②
- △PAE の面積が 2 回目に 36 cm2 になるのは、点 P が BE 上にあるとき。このとき、△PAE は底辺 PE、高さ AB ( 12 cm ) の三角形である。
面積が 36 cm2 のとき、
PE = 36 × 2 ÷ 12 = 6 [cm]
グラフより、点 P が B から E まで移動するのにかかる時間は 6 秒より、
BE = 1.5 × 6 = 9 [cm]
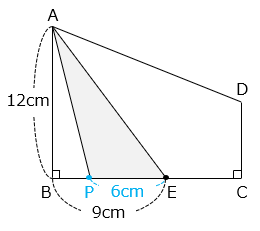
△PAE の面積が 2 回目に 36 cm2 になるのは、
( 12 + 3 ) ÷ 1.5 = 10 [秒後]
③ 点 P が A を出発してから、20秒後の三角形 PAE の面積を求めなさい。
- 答え(2)- ③
- 49.5 cm2
- 解き方(2)- ③
- 20 秒後点 P は、CD 上の C から 1.5 × 2 = 3 [cm] の位置にある。
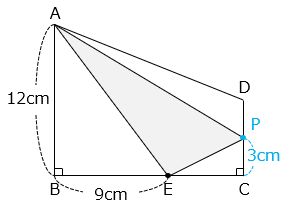
△PAE の面積は、□ABCP から △ABE と△PEC を除いた面積である。
□ABCP
= ( 12 + 3 ) × BC ÷ 2
= 15 × ( 1.5 × 10 ) ÷ 2
= 15 × 15 ÷ 2 = 112.5 [cm2]
△PEC
= 6 × 3 ÷ 2 = 9 [cm2]
グラフより、△ABE = 54 [cm2]
△PAE = 112.5 – 54 – 9 = 49.5 [cm2]
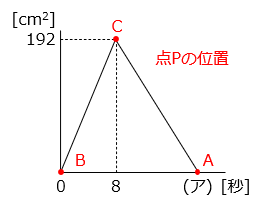
(3)図 1 のような直角三角形 ABC があります。点 P は B を出発し、B → C → A の順に毎秒 2 秒で辺上を移動します。図 2 のグラフは、点 P が B を出発してからの時間と三角形 ABP の面積の関係を表したものです。
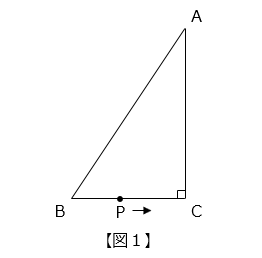

- ヒント
BC = 2 × 8 = 16 [cm]
① 辺 AC の長さは何 cm ですか。
- 答え(3)- ①
- 24 cm
- 解き方(3)- ①
- △ABC の面積は、点 P が C に来た時の△ABP の面積に等しい。
グラフより、BC の長さは、2 × 8 = 16 [cm]
よって、
AC = 192 × 2 ÷ 16 = 24 [cm]
② グラフの(ア)に当てはまる数はいくつですか。
- 答え(3)- ②
- 20
- 解き方(3)- ②
- 点 P が C から A に移動するのにかかる時間は、24 ÷ 2 = 12 [秒]
よって、
(ア)= 8 + 12 = 20
③ 三角形 ABP の面積が 144 cm2 になるのは、点 P が B を出発してから何秒後と何秒後ですか。
- 答え(3)- ③
- 6 秒後と 11 秒後
- 解き方(2)- ③
- △ABP の面積が 144 cm2 になるのは、点 P が BC 上にあるときと、CA 上にあるときの2回。
△ABP の面積が 144 cm2 のとき、△ABP:△ABC = 144:192 = 3:4 となる。
【点 P が BC 上にあるとき】
BP:BC = 3:4
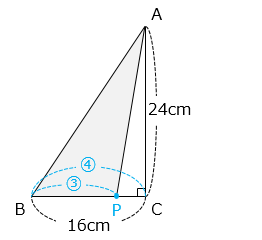
BP = 16 × \(\dfrac{3}{4}\) = 12 [cm]
よって、12 ÷ 2 = 6 [秒後]
【点 P が CA 上にあるとき】
AC:AP = 4:3、すなわち AC:PC = 4:1
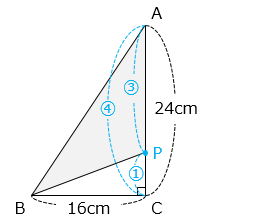
PC = 24 × \(\dfrac{1}{4}\) = 6 [cm]
よって、( 16 + 6 ) ÷ 2 = 11 [秒後]
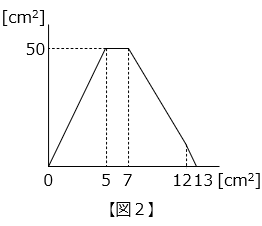
(4)図 1 のように、点 P は秒速 2 cm の速さで B を出発し、周上を B → C → D → E → A の順に移動します。図 2 は、点 P が出発してからの時間と、三角形 PAB の面積の関係を表したグラフです。
- ヒント
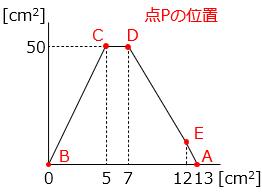
BC = 2 × 5 = 10 [cm]
CD = 2 × 2 = 4 [cm]
DE = 2 × 5 = 10 [cm]
EA = 2 × 1 = 2 [cm]
① CD の長さは何 cm ですか。
- 答え(4)- ①
- 4 cm
- 解き方(4)- ①
- 2 × 2 = 4 [cm]
② AB の長さは何 cm ですか。
- 答え(4)- ②
- 10 cm
- 解き方(4)- ②
- グラフより、点 P が C の位置にあるときの面積は 50 cm2 である。また、BC = 2 × 5 = 10 [cm] より、
AB = 50 × 2 ÷ 10 = 10 [cm]
③ 9 秒後の三角形 PAB の面積は何 cm2 ですか。
- 答え(4)- ③
- 34 cm2
- 解き方(4)- ③
- グラフより、DE = 10 [cm]、EA = 2 [cm]
9 秒後、点 P は DE 上の D から 2 × 2 = 4 [cm] の位置にある。
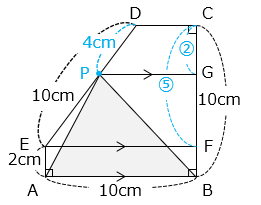
上図のように、F、G を取る。
DE:DP = CF:CG = 5:2 より、CF:GF = 5:3
よって、
GF
= CF × \(\dfrac{3}{5}\)
= 8 × \(\dfrac{3}{5}\) = 4.8 [cm]
△PAB
= 10 × ( 2 + 4.8 ) ÷ 2 = 34 [cm2]
問3
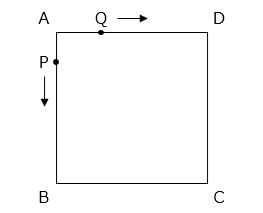
(1)図のような 1 辺が 15 cm の正方形 ABCD があります。この辺の上を点 P は毎秒 3 cm の速さで矢印に方向に動き、点 Q は毎秒 2 cm の速さで矢印の方向に動きます。P と Q が同時に点 A を出発するとき、出発後からかぞえて 8 回目に出会うのは辺 AB、BC、CD、DA のうち、どの辺の上ですか。
- 答え(1)
- 辺 AD
- 解き方(1)
- 正方形 ABCD の 1 周の長さは 15 × 4 = 60 (cm)
よって、P と Q は、60 ÷ ( 3 + 2 ) = 12 [秒] ごとに出会う。(出会い算)
8 回目に出会うのは、12 × 8 = 96 [秒後]
96 秒で Q が進む長さは、2 × 96 = 192 [cm]
192 ÷ 60 = 3 あまり 12
すなわち、Q は 3 周と 12 cm 進む。
よって、辺 AD 上で出会う。
※ P の進む長さで考えても良いが、小さい数の方が計算が簡単
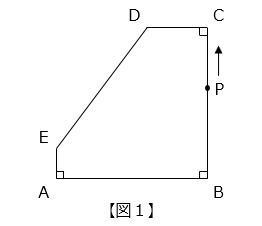
(2)図のような 1 辺が 6 cm の正方形 ABCD があります。2 点 P、Q が同時に頂点 A、B から反時計回りに、P は秒速 2 cm、Q は秒速 4 cm の速さで動きます。P、Q は P が再び A に戻るまで動きます。
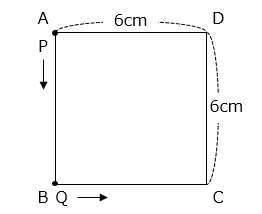
① 出発してから 2 秒後の 2 点 P、Q と頂点 A を結び、三角形を作ります。この三角形の面積を求めなさい。
- 答え(2)- ①
- 12 cm2
- 解き方(2)- ①
- 2 秒後、P は 2 × 2 = 4 [cm] 、Q は 4 × 2 = 8 [cm] 動いている。よって、P は AB 上の A から 4 cm の位置にあり、Q は CD 上の C から 2 cm の位置にある。
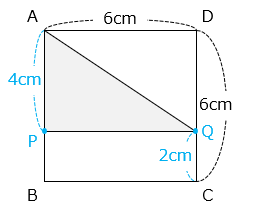
△APQ = 6 × 4 ÷ 2 = 12 [cm2]
② 2 点 P、Q が重なるのは、出発してから何秒後ですか。
- 答え(2)- ②
- 9 秒後
- 解き方(2)- ②
- 追いかけ算と考える。P と Q は 6 × 3 = 18 [cm] 離れているので、
18 ÷ ( 4 – 2 ) = 9 [秒後]
③ P が再び A に戻るまでの間に、2 点 P、Q と頂点 A を結んで三角形ができない時間は、出発時の 0 秒と出発してから 4.5 秒後の他に、何秒後から何秒後までの間ですか。
- 答え(2)- ③
- 9 秒後から 10.5 秒後
- 解き方(2)- ③
- 出発してから 4.5 秒後は、Q と A が初めて重なるとき。
0 秒後と 4.5 秒後以外で三角形ができない時間は、P と Q が重なったときと、P と Q が共に AD 上にあり、A と P と Q が直線上になるとき。
①より、P と Q が重なる位置は、P が 2 × 9 = 18 [cm] 動いたときなので、 D にあるとき。よって、このときから Q が A に着くまでの時間三角形はできない。Q が A に着くまでにかかる時間は、
6 ÷ 4 = 1.5 [秒]
したがって、9 秒後から 10.5 秒後までの間、三角形はできない。
(3)図のような 1 辺が 1 cm の正六角形 ABCDEF があります。点 P は A を出発して、A → B → C → D → E → F → A の順に移動します。点 Q は A を出発して、A → B → G → E → F → A の順に移動します。P、Q はともに毎秒 1 cm の速さで同時に A を出発します。
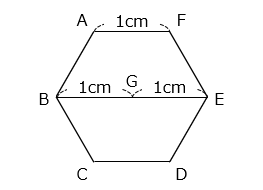
① 点 P、Q が出発した後、初めて A を同時に通過するのは何秒後ですか。
- 答え(3)- ①
- 30 秒後
- 解き方(3)- ①
- P が 1 周して A に戻るのにかかる時間は、6 ÷ 1 = 6 [秒]
Q が 1 周して A に戻るのにかかる時間は、5 ÷ 1 = 5 [秒]
出発後初めて同時に A を通過するのは、P、Q がそれぞれ A に戻るのにかかる時間の最小公倍数となるので、30 秒後。
② 点 P、Q が 1 分 40 秒間動き続けたとき、重なって移動するのは合わせて何秒間ですか。
- 答え(3)- ②
- 10 秒間
- 解き方(3)- ②
- P、Q が同時に A を通過するのは、30 秒に 1 回。この間 P、Q が重なって移動するのは、 A → B を通過する最初の 1 秒と、E → F → A を通過する最後の 2 秒の 3 秒間。
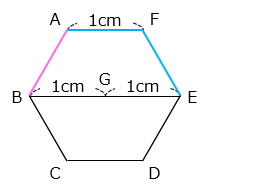
1 分 40 秒 = 30 秒 × 3 あまり 10 秒
よって、重なって移動できる時間は、3 周と10秒となる。
4周目の最初の10秒間は、A → B は重なっているので、
3 × 3 + 1 = 10 [秒間]

































