算数【入試】余りのある計算

問１

大、小2つの整数があり、その差は75です。また、大きい整数を小さい整数で割ると、商が5で余りが7になりました。大、小2つの整数をそれぞれ求めなさい。

答え

大きい整数 92, 小さい整数 17

解き方

線分図にすると、

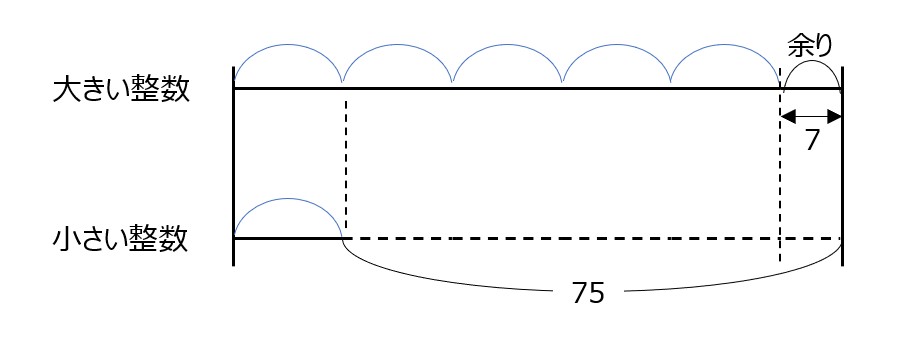
小さい整数は、(75 – 7) ÷ 4 = 17
大きい整数は、17 × 5 + 7 = 92

＜別解＞
大きい整数を□とすると、小さい整数は□ – 75となる。除法の原理より、
□ = 5 × (□ – 75) + 7
□ = 92
よって、小さい整数は92 – 75 = 17

問２

あめを4個ずつ箱はこに入れたところ、箱が2つ足りないことがわかりました。そこで、箱に入らなかったあめを1個ずつ、4個ずつ入っている箱に入れていきました。すると、4個ずつ入っている箱と5個ずつ入っている箱の数の比が5 : 3になりました。あめは何個ありますか。

答え

70個

解き方

あめを4個ずつ箱に入れたときのあめの余りは5個以上8個以下となる。
箱の数の比5：3から箱の数を一番簡単な⑧個とすると、あめが4個入った箱の数は⑤、あめが5個入った箱の数は③と表すことができる。
5個以上8個以下の数で3の倍数は6だけなので、③ = 6より、① = 2となる。
よって、4個入りの箱の数は、⑤ × 2 = 10（箱）
5個入りの箱の数は、③ × 2 = 6（箱）となる
あめの個数は、4 × 10 + 5 × 6 = 70（個）

＜別解＞
あめを4個ずつ箱に入れたときの余りは5個以上8個以下となる。箱の数を⑧とすると、あめの個数は、
4 × ⑤ + 5 × ③ = 4 × ⑧ + 余り
すなわち、余りは③とあらわされる。
余りは5以上8以下であることから③ = 6であることがわかり、あめの個数は㉟ × 2 = 70(個)

問３

641を割ると11余り、555を割ると9余る整数をすべて求めなさい。

答え

42, 21, 14

解き方

641を割ると11余り、555を割ると9余る数は、641 – 11 = 630と、555 – 9 = 546の公約数のうち余りより大きい数となる。630と546の最大公約数は42となるので、42の約数のうち11より大きい、42、21、14となる。

問４

ある数を21で割ると余りが17になりました。同じ数を23で割ると、商は21で割ったときと同じになり、余りは3でした。ある数を求めなさい。

答え

164

解き方

商をaとすると、ある数はa × 21 + 17 = a × 23 + 3と表せるので、a = \(\dfrac{17 – 3}{23 – 21}\) = 7となる。したがって、ある数は7 × 21 + 17 = 164

問５

4で割っても、5で割っても、6で割っても2余るような7の倍数の中で、小さいほうから2番目の数を求めなさい。

答え

602

解き方

4と5と6の最小公倍数の60で割ると2余る数の中で、もっとも小さい7の倍数は数は182である。その後は、60と7の最小公倍数420ごとにあらわれるので、2番目は182 + 420 = 602