算数【基本】場合の数(順列・組み合わせ・図形)
問1
(1)3 cm、4 cm、5 cm、6 cm、8 cmのまっすぐな棒から 3 本取り出して、三角形を作るとき、何通りの三角形ができますか。
- 答え(1)
- 8 通り
- 解き方(1)
- 3 本の棒で三角形をつくる場合、最も長い辺は、残りの 2 辺の和より小さくなければならない。
最も長い辺が 8 cmのとき、残り 2 辺の長さ組み合わせは、(3, 6)、(4, 5)、(4, 6)、(5, 6) の4通り
最も長い辺が 6 cmのとき、残り2辺の長さ組み合わせは、(3, 4)、(3, 5) 、(4, 5) の 3 通り
最も長い辺が 5 cmのとき、残り 2 辺の長さ組み合わせは、(3, 4) の 1 通り
よって全部で 4 + 3 + 1 = 8 [通り] (2)\(\boxed{3}\)、\(\boxed{4}\)、\(\boxed{5}\)、\(\boxed{6}\) の 4 枚のカードから 2 枚を取り出して 2 けたの整数をつくります。その中に 46 より大きい偶数は何個ありますか。
- 答え(2)
- 3 個
- 解き方(2)
- 十の位が 4 で 46 より大きい偶数はない。
十の位が 5 で 46 より大きい偶数は 54、56 の 2 個
十の位が 6 で 46 より大きい偶数は 64 の 1 個
よって、2 + 1 = 3 [個]
問2 順列、組み合わせ(計算で求める)
- 順列と組み合わせとは
- ●順列:異なるいくつかのものから条件に合うものを選んで順に並べること
異なる N 個のものから異なる n 個を選んで並べる順列の総数は、

●組み合わせ:異なるいくつかのものから何個かを選ぶこと
異なる N 個の中から異なる n 個を取り出す組み合わせの総数は、

(1)\(\boxed{あ}\)、\(\boxed{い}\)、\(\boxed{う}\)、\(\boxed{え}\)、\(\boxed{お}\) の 5 枚のカードを 1 列に並べる方法は何通りありますか。
- 答え(1)
- 120 通り
- 解き方(1)
- 一枚目のカードを選ぶとき、5 枚から 1 枚選ぶので 5 通り
二枚目のカードを選ぶとき、残り 4 枚から 1 枚選ぶので 4 通り
同様に三枚目、四枚目、最後五枚目は残り 1 枚なので 1 通りとなり、
5 × 4 × 3 × 2 × 1 = 120 [通り] となる (2)A、B、C、D、E の 5 人が縦一列に並びます。先頭に A が並ばないとき、並び方は全部で何通りありますか。
- 答え(2)
- 96 通り
- 解き方(2)
- 先頭を選ぶ方法は A 以外の B、C、D、E の 4 人から選択するので 4 通り
二番目を選ぶ方法は残り 4 人の中から選ぶので 4 通り
同様に三番目は 3 通り、四番目は 2 通り、最後の 1 人は 1 通りとなり
4 × 4 × 3 × 2 × 1 = 96 [通り] (3)男子 3 人と女子 3 人が一列に並んで写真を撮ります。このとき、男女交互に並ぶ並び方は、全部で何通りありますか。ただし、男女 6 人は区別して考えること。
- 答え(3)
- 72 通り
- 解き方(3)
- 最初が男子の場合、3 × 3 × 2 × 2 × 1 × 1 = 36 [通り]
最初が女子の場合、3 × 3 × 2 × 2 × 1 × 1 = 36 [通り]
よって、36 + 36 = 72 [通り] (4)\(\boxed{2}\)、\(\boxed{3}\)、\(\boxed{4}\)、\(\boxed{6}\) の 4 枚のカードを並べて 4 けたの整数をつくります。偶数は何個できますか。
- 答え(4)
- 18 個
- 解き方(4)
- 4 けたの整数は全部で 4 × 3 × 2 × 1 = 24 [個] できる。
そのうち、奇数になるのは一の位が \(\boxed{3}\) のときだけなので、3 × 2 × 1 × 1 = 6 [個]
よって偶数は、24 – 6 = 18 [個] (5)0、1、3、5 を使って、3 けたの整数を作ります。同じ数字を何度使ってもよいことにすると、整数は全部で何通りできますか。
- 答え(5)
- 48 通り
- 解き方(5)
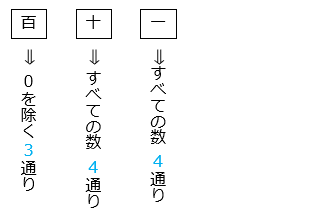
3 × 4 × 4 = 48 [通り](6)A、B、C、D、E の 5 人の中から、委員を 3 人選びます。選び方は何通りありますか。
- 答え(6)
- 10 通り
- 解き方(6)
- \(\dfrac{5\ ×\ 4\ ×\ 3}{3\ ×\ 2\ ×\ 1}\) = 10 [通り]
(7)A ~ E の 5 組のチームで試合を行いました。必ず全チームと 1 度は試合を行い、同じチームと 2 度は試合をしません。試合は全部で何試合ありますか。
- 答え(7)
- 10 試合
- 解き方(7)
- 試合の数 = 5 組から 2 組を選ぶ組み合わせの数
\(\dfrac{5\ ×\ 4}{2\ ×\ 1}\) = 10 [試合] (8)\(\boxed{0}\)、\(\boxed{4}\)、\(\boxed{5}\)、\(\boxed{5}\) の 4 枚のカードを並べてできる 4 桁の数は何個ありますか。
- 答え(8)
- 9 通り
- 解き方(8)
- まず、2 枚ある \(\boxed{5}\) を区別して考えると( \(\boxed{5}\)1, \(\boxed{5}\)2 )、
3 × 3 × 2 × 1 = 18 [通り]
\(\boxed{5}\)1 と \(\boxed{5}\)2 の並び方は 2 × 1 = 2 [通り] あるが、実際はこれらのカードは区別できない。
よって、18 ÷ 2 = 9 [通り]
実際に書き出すと以下の通り。
\(\boxed{4}\) \(\boxed{0}\) \(\boxed{5}\)1 \(\boxed{5}\)2 = \(\boxed{4}\) \(\boxed{0}\) \(\boxed{5}\)2 \(\boxed{5}\)1
\(\boxed{4}\) \(\boxed{5}\)1 \(\boxed{0}\) \(\boxed{5}\)2 = \(\boxed{4}\) \(\boxed{5}\)2 \(\boxed{0}\) \(\boxed{5}\)1
\(\boxed{4}\) \(\boxed{5}\)1 \(\boxed{5}\)2 \(\boxed{0}\) = \(\boxed{4}\) \(\boxed{5}\)2 \(\boxed{5}\)1 \(\boxed{0}\)
\(\boxed{5}\)1 \(\boxed{0}\) \(\boxed{4}\) \(\boxed{5}\)2 = \(\boxed{5}\)2 \(\boxed{0}\) \(\boxed{4}\) \(\boxed{5}\)1
\(\boxed{5}\)1 \(\boxed{0}\) \(\boxed{5}\)2\(\boxed{4}\) = \(\boxed{5}\)2 \(\boxed{0}\) \(\boxed{5}\)1 \(\boxed{4}\)
\(\boxed{5}\)1 \(\boxed{4}\) \(\boxed{0}\) \(\boxed{5}\)2 = \(\boxed{5}\)2 \(\boxed{4}\) \(\boxed{0}\) \(\boxed{5}\)1
\(\boxed{5}\)1 \(\boxed{4}\) \(\boxed{5}\)2 \(\boxed{0}\) = \(\boxed{5}\)2 \(\boxed{4}\) \(\boxed{5}\)1 \(\boxed{0}\)
\(\boxed{5}\)1 \(\boxed{5}\)2 \(\boxed{0}\) \(\boxed{4}\) = \(\boxed{5}\)2 \(\boxed{5}\)1 \(\boxed{0}\) \(\boxed{4}\)
\(\boxed{5}\)1 \(\boxed{5}\)2 \(\boxed{4}\) \(\boxed{0}\) = \(\boxed{5}\)2 \(\boxed{5}\)1 \(\boxed{4}\) \(\boxed{0}\)
※同じ数字を複数含む場合の並べ方の個数は、すべての数字の並び方の個数を、複数ある数字の並び方の個数で割った個数になる。 (9)\(\boxed{5}\)、\(\boxed{6}\)、\(\boxed{7}\)、\(\boxed{8}\)、\(\boxed{9}\) の 5 枚のカードから 3 枚を取り出して並べ、3 けたの整数を作ります。5 の倍数は何個作れますか。
- 答え(9)
- 12 個
- 解き方(9)
- これらのカードで 5 の倍数を作る場合、一の位が必ず \(\boxed{5}\) である。
百の位は \(\boxed{5}\) 以外の 4 通り、十の位は 3 通りなので、
4 × 3 × 1 = 12 [個] (10)0、1、2、5、8、9 のうち異なる 3 個を並べて、3 けたの整数を作ります。5 の倍数は全部で何個できますか。
- 答え(10)
- 36 個
- 解き方(10)
- これらの数字で 5 の倍数を作る場合、一の位は 0 か 5 である。
一の位が 0 のときは、5 × 4 × 1 = 20 [個]
一の位が 5 のときは、4 × 4 × 1 = 16 [個]
全部で 20 + 16 = 36 [個] (11)\(\boxed{0}\)、\(\boxed{1}\)、\(\boxed{2}\)、\(\boxed{4}\) の 4 枚のカードから 3 枚を選び、3 けたの整数を作ります。3 の倍数は何通りできますか。
- 答え(11)
- 8 通り
- 解き方(11)
- 3 の倍数は各位の数字の和が 3 の倍数となる。
3 つの数字の和が 3 の倍数になる組み合わせは、(0, 1, 2)、(0, 2, 4) の 2 通り。
0 を含む 3 つの数字でできる 3 けたの整数は、2 × 2 × 1 = 4 [通り]
よって、4 × 2 = 8 [通り] (12)\(\boxed{2}\)、\(\boxed{2}\)、\(\boxed{3}\)、\(\boxed{・}\) の 4 枚のカードから 3 枚を取り出して並べ、数を作ります。\(\boxed{・}\) は小数点です。全部で何個作れますか。
- 答え(12)
- 6 個
- 解き方(12)
- 小数点を含まない取り出し方の組み合わせは、\(\boxed{2}\)、\(\boxed{2}\)、\(\boxed{3}\) の 1 通り
このときのできる数の個数は、3 × 2 × 1 ÷ 2 = 3[個]
※ \(\boxed{2}\) が 2 つあり、その並び方が 2 通りあるから
小数点を含む取り出し方の組み合わせは、\(\boxed{・}\)、\(\boxed{2}\)、\(\boxed{2}\) と \(\boxed{・}\)、\(\boxed{2}\)、\(\boxed{3}\) の 2 通り
\(\boxed{・}\)、\(\boxed{2}\)、\(\boxed{2}\) のときできる数は、2.2 の 1 個
\(\boxed{・}\)、\(\boxed{2}\)、\(\boxed{3}\) のときできる数は、2.3 と 3.2 の 2 個
(小数点が最初と最後にくることはない)
よって、全部で 3 + 1 + 2 = 6 [個] (13)A、B、C の 3 グループで動物園、水族館、遊園地に行くことになりました。1 か所に 2 グループまで行くことができるとき、行先の組み合わせは全部で何通りありますか。どのグループも行かない場所があってもよいとします。
- 答え(13)
- 24 通り
- 解き方(13)
- ① 3 グループとも行先が異なる場合
3 × 2 × 1 = 6 [通り]
② 2 つグループの行先が同じ場合
行先が同じとなる 2 グループの組み合わせは、\(\dfrac{3\ ×\ 2}{2\ ×\ 1}\) = 3 [通り]
このとき、もう一つのグループは 2 通りの行先があるので、3 × 2 = 6
実際に記述してみると下表のようになる。
| A | B | C | |
| 動 | 動 | 水
遊 | 2通り |
| 動 | 水
遊 | 動 | 2 通り |
水
遊 | 動 | 動 | 2 通り |
行先が同じとなる 2 グループは動物園、水族館、遊園地の 3 通りあるので、6 × 3 = 18 [通り]
①② を合わせて、6 + 18 = 24 [通り] (14)階段を上るとき、「1 歩で 1 段」、または「1 歩で 2 段」の 2 通りの方法を組み合わせて上ることにします。
① 6 段の階段を上る方法は全部で何通りありますか。
- 答え(14)- ①
- 13 通り
- 解き方(14)- ①
- 6 段の階段を登るときの 1 歩の段数の組み合わせは、(1, 1, 1, 1, 1, 1)、(2, 1, 1, 1, 1)、(2, 2, 1, 1)、(2, 2, 2)
順番について考えると、
(1, 1, 1, 1, 1, 1) ⇒ 1 通り
(2, 1, 1, 1, 1) ⇒ \(\dfrac{5\ ×\ 4\ ×\ 3\ ×\ 2\ ×\ 1}{4\ ×\ 3\ ×\ 2\ ×\ 1}\) = 5 [通り]
(2, 2, 1, 1) ⇒ \(\dfrac{4\ ×\ 3\ ×\ 2\ ×\ 1}{2\ ×\ 1\ ×\ 2\ ×\ 1}\) = 6 [通り]
(2, 2, 2) ⇒ 1 通り
よって全部で 1 + 5 + 6 + 1 = 13 [通り]
※同じ数字を複数含む場合の並べ方の個数は、すべての数字の並び方の個数を、複数ある数字の並び方の個数で割った個数になる。 ② 12 段の階段があります。この階段の 5 段目をふまずに 9 歩で上る方法は、全部で何通りありますか。
- 答え(14)- ②
- 22 通り
- 解き方(14)- ②
- 12 段の階段を 9 歩で登るときの段数の組み合わせは、(2, 2, 2, 1, 1, 1, 1, 1, 1) のみである。
また、5 段目はふめないので、4 段目の次の 1 歩は必ず 2 段となる。
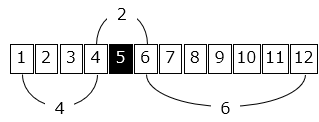
1~4段目(4段)までの 1 歩の段数の組み合わせ(左)と、6~12段目(6段)までの 1 歩の段数の組み合わせ(右)を考えると、
(1, 1, 1, 1)と(2, 2, 1, 1) ⇒ 1 × \(\dfrac{4\ ×\ 3\ ×\ 2\ ×\ 1}{2\ ×\ 1\ ×\ 2\ ×\ 1}\) = 6 [通り]
(2, 1, 1)と(2, 1, 1, 1, 1) ⇒ \(\dfrac{3\ ×\ 2\ ×\ 1}{2\ ×\ 1}\) × \(\dfrac{5\ ×\ 4\ ×\ 3\ ×\ 2\ ×\ 1}{4\ ×\ 3\ ×\ 2\ ×\ 1}\) = 3 × 5 = 15 [通り]
(2, 2) と (1, 1, 1, 1, 1, 1) ⇒ 1 × 1 = 1 [通り]
よって全部で 6 + 15 + 1 = 22 [通り]
※同じ数字を複数含む場合の並べ方の個数は、すべての数字の並び方の個数を、複数ある数字の並び方の個数で割った個数になる。
問3 図形
(1)図のように長方形を 3 つの部分にぬり分けます。このとき、となり合う場所は異なる色になるようにします。
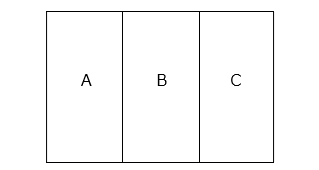
① 赤、白の 2 色でぬり分けるとき、何通りのぬり方がありますか。
- 答え(1)- ①
- 2 通り
- 解き方(1)- ①
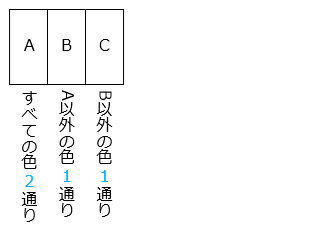
2 × 1 × 1 = 2 [通り]② 赤、白、青の 3 色でぬり分けるとき、何通りのぬり方がありますか。
- 答え(1)- ②
- 6 通り
- 解き方(1)- ②
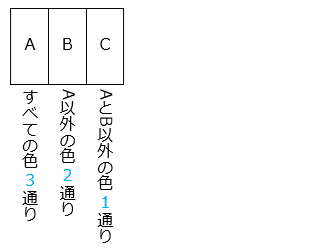
3 × 2 × 1 = 6 [通り]③ 赤、白、青の 3 色でぬり分けるとき、何通りのぬり方がありますか。ただし、使わない色があってもよいものとします。
- 答え(1)- ③
- 12 通り
- 解き方(1)- ③
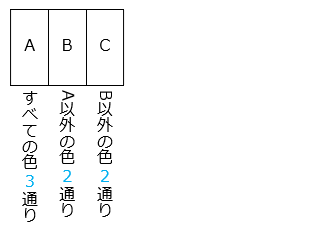
3 × 2 × 2 = 12 [通り]④ 赤、白、青、黄の 4 色から 3 色を選んでぬり分けるとき、何通りのぬり方がありますか。
- 答え(1)- ④
- 24 通り
- 解き方(1)- ④
- A はすべての色の 4 通り、B は A 以外の色の 3 通り、C は A と B 以外の色の 2 通りなので、
4 × 3 × 2 = 24 [通り] (2)A 地点から遠まわりをしないで B 地点まで行く方法を考えます。
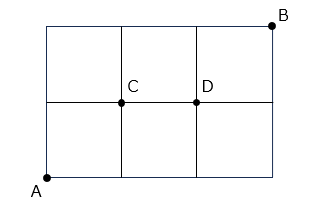
- ヒント(2)
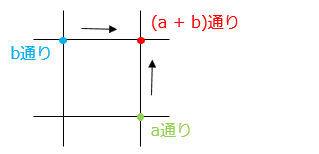
和の法則より、ある点(●)までの行き方は 1 つ手前の点(●, ●)までの行き方の和となります。
交差点ごとに行き方の数を書き込んでいきましょう!① 全部で何通りの方法がありますか。
- 答え(2)- ①
- 10 通り
- 解き方(2)- ①
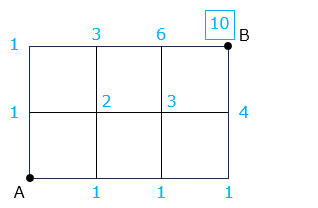
図より、10 通り② A 地点から C 地点を通って、B 地点まで行く方法は何通りありますか。
- 答え(2)- ②
- 6 通り
- 解き方(2)- ②
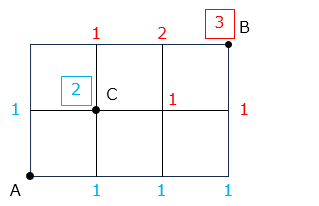
図より、A 地点から C 地点に行く方法は 2 通り、C 地点から B 地点に行く方法は3 通りなので、
2 × 3 = 6 [通り]③ C 地点と D 地点を結ぶ道を通らずに、B 地点まで行く方法は何通りありますか。
- 答え(2)- ③
- 6 通り
- 解き方(2)- ③
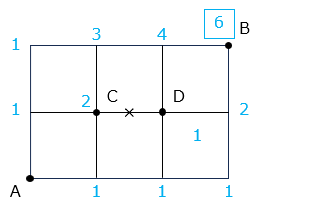
図より、6 通り(3)頂点Aから辺を通って頂点Bに最短で行く方法は何通りありますか。
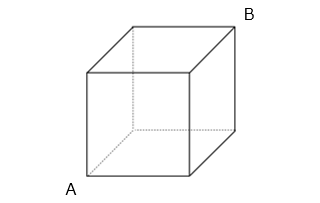
- 答え(3)
- 6 通り
- 解き方(3)
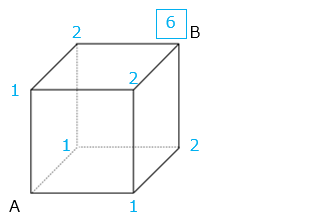
※2 辺が合流する点は 2 つの数の和、3 辺が合流する点は 3 つの数の和
図より、6 通り(4)図のように 1 辺の長さが 1 cmの正方形 15 個からできた長方形があります。
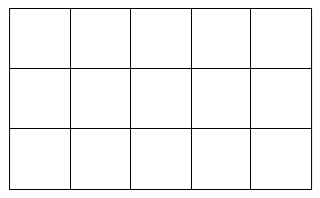
① この図の中に、1 辺が 2 cmの正方形は全部で何個ありますか。
- 答え(4)- ①
- 8 個
- 解き方(4)- ①
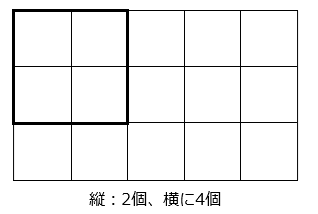
図より、縦に 2 個、横に 4 個できるので、2 × 4 = 8 [個]② この図の中に、正方形は全部で何個ありますか。
- 答え(4)- ②
- 26 個
- 解き方(4)- ②
- 最も小さい 1 辺 1 cmの正方形は 15 個
1 辺 2 cmの正方形は ① より 8 個
最も大きい 1 辺 3 cmの正方形は 1 × 3 = 3 [個]
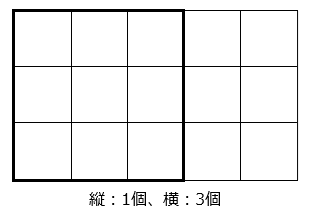
全部で、15 + 8 + 3 = 26 [個]


















