算数【応用】倍数算

問１

（１）A さんと B さんの持っているお金の比は 2：1 で、2 人のお金は合わせて 4140 円です。2 人が同じ値段のアクセサリーを買ったところ、お金の比は 5：2 になりました。アクセサリーの代金は 1 個いくらですか。

答え（１）: 460 円

解き方（１）: A さんと B さんは同じ値段のアクセサリーを買ったので、買う前後で所持金の差は変化していない。

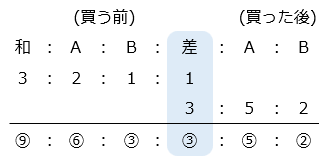
買う前の 2 人のお金の和は ⑨、アクセサリーの代金は A さん（または B さん）の買う前後のお金の差なので、⑥ – ⑤ = ① となる。
⑨ = 4140
① = 460 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
アクセサリーを買う前の所持金は、
A さん、4140 × \(\dfrac{2}{3}\) = 2760 [円]
B さん、4140 – 2760 = 1380 [円]
アクセサリーの代金を □ 円とすると、
2760 – □：1380 – □ = 5：2
5 × ( 1380 – □ ) = 2 × ( 2760 – □ )
□ = 460 [円]

（２）A さんと B さんの所持金の比は 2：3 です。2 人とも 780 円使ったところ、A さんと B さんの所持金の比は 3：11 になりました。A さんのはじめの所持金はいくらですか。

答え（２）: 960 円

解き方（２）: A さんと B さんは同じ金額を使ったので、買う前後で所持金の差は変化していない。

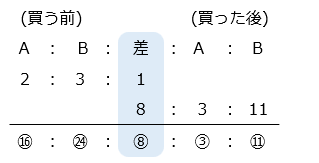
A さんのはじめの所持金は ⑯、使ったお金は ⑯ – ③ = ⑬より、
⑬ = 780
① = 60 [円]
A さんのはじめの所持金は、⑯ = 16 × 60 = 960 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
A さんのはじめの所持金を ② とすると、B さんのはじめの所持金は ③ と表すことができる。よって、
② – 780：③ – 780 = 3：11
3 × ( ③ – 780 ) = 11 × ( ② – 780 )
① = 480
A さんのはじめの所持金は、② = 2 × 480 = 960 [円]

（３）姉と妹の所持金の比は 9：4 でしたが、姉が妹に 300 円渡したので、姉と妹の所持金の比は 3：2 になりました。姉のはじめの所持金はいくらですか。

答え（３）: 2250 円

解き方（３）: 姉が妹にお金を渡す前後で、姉と妹の所持金の和は変化していない。

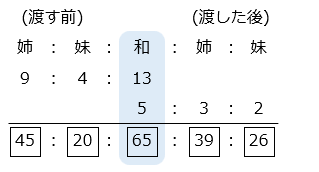
\(\boxed{45}\) – \(\boxed{39}\) = 300
\(\boxed{1}\) = 50
姉のはじめの所持金は、
\(\boxed{45}\) = 45 × 50 = 2250 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
姉のはじめに所持金を \(\boxed{9}\) とすると、妹は \(\boxed{4}\) と表すことができる。よって、
\(\boxed{9}\) – 300：\(\boxed{4}\) + 300 = 3：2
3 × ( \(\boxed{4}\) + 300 ) = 2 × ( \(\boxed{9}\) – 300 )
\(\boxed{1}\) = 250
姉のはじめの所持金は、\(\boxed{9}\) = 9 × 250 = 2250 [円]

（４）兄と弟が最初に持っていた金額の比は 13：5 でした。2 人とも 500 円ずつおこずかいをもらったところ、2 人の所持金の比は 7：3 になりました。兄の最初の所持金はいくらですか。

答え（４）: 6500 円

解き方（４）: おこずかいをもらう前後で、兄と弟の所持金の差は変化していない。

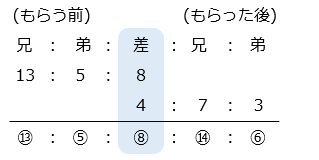
⑭ – ⑬ = ① = 500
兄の最初の所持金は、⑬ = 13 × 500 = 6500 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
兄の最初の所持金を ⑬ とすると、弟は ⑤ と表すことができる。よって、
⑬ + 500：⑤ + 500 = 7：3
7 × ( ⑤ + 500 ) = 3 × ( ⑬ + 500 )
① = 500
兄の最初の所持金は、⑬ = 13 × 500 = 6500 [円]

（５）あめがいくつかあります。A 君と B 君で分けたところ、個数の比は 3：2 になりました。その後、A 君が B 君にあめを 15 個あげたら、個数の比は 3：7 になりました。あめは全部で何個ありますか。

答え（５）: 50 個

解き方（５）: A 君が B 君にあめをあげる前後で、あめの全個数は変化していない。

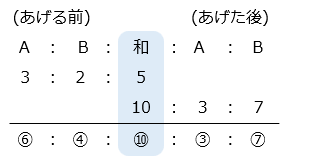
⑥ – ③ = 15
① = 5
あめの全個数は、⑩ = 10 × 5 = 50 [個]

別の計算方法【内項の積 = 外項の積で求める方法】
A 君があめをあげる前の個数を ③ とすると、B 君の個数は ② と表すことができる。よって、
③ – 15：② + 15 = 3：7
3 × ( ② + 15 ) = 7 × ( ③ – 15 )
① = 10
あめの全個数は、③ + ② = ⑤ = 5 × 10 = 50 [個]

（６）兄と弟の所持金の比は、はじめ 3：1 でしたが、2 人とも 150 円のお菓子を買ったので、2 人の所持金の比が 5：1 になりました。兄のはじめの所持金はいくらでしたか。

答え（６）: 900 円

解き方（６）: 兄と弟は同じ金額を使ったので、買う前後で所持金の差は変化していない。

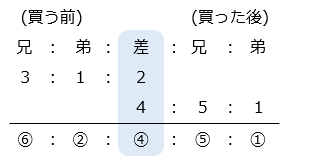
兄のはじめの所持金は⑥、使ったお金は ⑥ – ⑤ = ① = 150より、
兄のはじめの所持金は、⑥ = 6 × 150 = 900 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
兄のはじめの所持金を ③ とすると、弟のはじめの所持金は ① と表すことができる。よって、
③ – 150：① – 150 = 5：1
5 × ( ① – 150 ) = ③ – 150
① = 300
兄のはじめの所持金は、③ = 3 × 300 = 900 [円]

（７）A さんと B さんの所持金の比は 7：5 でしたが、2 人とも 1200 円ずつ使ったので、所持金の比は 11：7 になりました。はじめに A さんは何円持っていましたか。

答え（７）: 5600円

解き方（７）: A さんと B さんは同じ金額を使ったので、使う前後で所持金の差は変化していない。

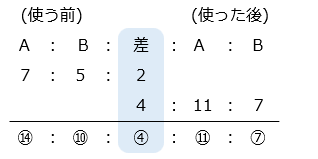
A さんのはじめの所持金は ⑭、使ったお金は ⑭ – ⑪ = ③ = 1200より、① = 400
A さんのはじめの所持金は、⑭ = 14 × 400 = 5600 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
A さんのはじめの所持金を ⑦ とすると、B さんのはじめの所持金は ⑤ と表すことができる。よって、
⑦ – 1200：⑤ – 1200 = 11：7
11 × ( ⑤ – 1200 ) = 7 × ( ⑦ – 1200 )
① = 800
A さんのはじめの所持金は、⑦ = 7 × 800 = 5600 [円]

（８）A さんと B さんの所持金の比は 7：2 でした。A さんから B さんに 500 円渡したら、2 人の所持金の比は 5：4 になりました。はじめに A さんと B さんはそれぞれ何円持っていましたか。

答え（８）: Aさん：1750 円　Bさん：500 円

解き方（８）: A さんから B さんにお金を渡す前後で、2人の所持金の和は変化していない。

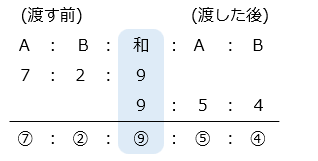
⑦ – ⑤ = 500
① = 250
A さんのはじめの所持金は、⑦ = 7 × 250 = 1750 [円]
B さんのはじめの所持金は、② = 2 × 250 = 500 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
A さんのはじめに所持金を ⑦ とすると、B さんは ② と表すことができる。よって、
⑦ – 500：② + 500 = 5：4
5 × ( ② + 500 ) = 4 × ( ⑦ – 500 )
① = 250
A さんのはじめの所持金は、⑦ = 7 × 250 = 1750 [円]
B さんのはじめの所持金は、② = 2 × 250 = 500 [円]

（９）兄と弟の年れいの比は現在 7：4 で、10 年後には 4：3 になります。現在、兄は何才ですか。

答え（９）: 14 才

解き方（９）: 兄と弟の年れいの差は、現在も 10 年後もかわらない。

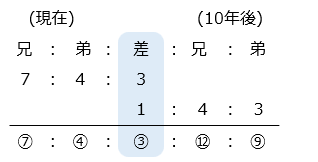
⑫ – ⑦ = ⑤ = 10
① = 2
兄の現在の年れいは、⑦ = 7 × 2 = 14 [才]

別の計算方法【内項の積 = 外項の積で求める方法】
兄の現在の年れいを ⑦ とすると、弟は ④ と表すことができる。よって、
⑦ + 10：④ + 10 = 4：3
4 × ( ④ + 10 ) = 3 × ( ⑦ + 10 )
① = 2
兄の現在の年れいは、⑦ = 7 × 2 = 14 [才]

（１０）2 種類の消しゴム A、B が売られています。はじめ個数の比は 4：3 でしたが、どちらも同じ数が売れたので、個数の比は 5：3 になり、個数の合計は 16 個になりました。A、B は何個ずつ売れましたか。

答え（１０）: 6 個

解き方（１０）: 同じ個数が売れたので、売れる前後の個数の差は変化しない。

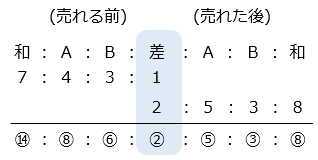
⑧ = 16
① = 2
A（または B ）の売れた個数は、⑧ – ⑤ = ③ = 3 × 2 = 6 [個]

別の計算方法【内項の積 = 外項の積で求める方法】
売れた後の A、B の個数は、
A：16 × \(\dfrac{5}{8}\) = 10 [個]
B：16 × \(\dfrac{3}{8}\)= 6 [個]
よって、売れた個数を □ とすると、
10 + □：6 + □ = 4：3
4 × ( 6 + □ ) = 3 × ( 10 + □ )
□ = 6 [個]

問２

（１）ノート A と B の冊数の比が 3：5 で売られています。ノート B が 6 冊売れたので補充しようとしたら在庫がありませんでした。代わりにノート A を 10 冊補充したところ、ノート A と B の冊数の比が 11：7 になりました。はじめにノート A と B はそれぞれ何冊売られていましたか。

答え（１）: A：12 冊　B：20 冊

解き方（１）: ノート A と B の冊数の比の変化を線分図で表し、変化後の比の大きさをそろえると、

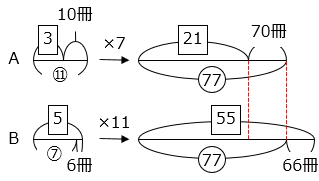
\(\boxed{55}\) – \(\boxed{21}\) = 70 + 66
\(\boxed{34}\) = 136
\(\boxed{1}\) = 4
はじめに売られていた冊数は、
ノート A：\(\boxed{3}\) = 3 × 4 = 12 [冊]
ノート B：\(\boxed{5}\) = 5 × 4 = 20 [冊]

別の計算方法【内項の積 = 外項の積で求める方法】
はじめに売られていたノート A の冊数を \(\boxed{3}\) とすると、B は \(\boxed{5}\) と表すことができる。よって、
\(\boxed{3}\) + 10：\(\boxed{5}\) – 6 = 11：7
11 × ( \(\boxed{5}\) – 6 ) = 7 × ( \(\boxed{3}\) + 10 )
\(\boxed{1}\) = 4
はじめに売られていた冊数は、
ノート A：\(\boxed{3}\) = 3 × 4 = 12 [冊]
ノート B：\(\boxed{5}\) = 5 × 4 = 20 [冊]

（２）A さんと B さんの所持金の比は 8：5 でしたが、A さんが 320 円を使ったので、その比が 4：3 になりました。A さんのはじめの所持金はいくらですか。

答え（２）: 1920 円

解き方（２）: A さんと B さんの所持金の比の変化を線分図で表し、変化後の比の大きさをそろえると、

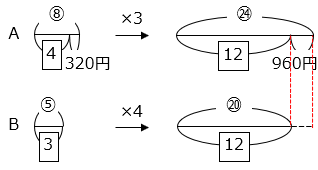
㉔ – ⑳ = 960
① = 240
A さんのはじめの所持金は、⑧ = 8 × 240 = 1920 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
A さんのはじめの所持金を ⑧ とすると、B さんは ⑤ と表すことができる。よって、
⑧ – 320：⑤ = 4：3
4 × ⑤ = 3 × ( ⑧ – 320 )
① = 240
A さんのはじめの所持金は、⑧ = 8 × 240 = 1920 [円]

（３）先月の兄と弟の貯金額の比は 1：2 でしたが、今月は兄は 600 円貯金して、弟は貯金から 200 円使ったところ、貯金額の比が 5：3 になりました。先月までの兄の貯金額はいくらですか。

答え（３）: 400 円

解き方（３）: 兄と弟の貯金額の比の変化を線分図で表し、変化後の比の大きさをそろえると、

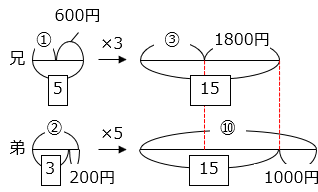
⑩ – ③ = 1800 + 1000
① = 400
先月までの兄の貯金額は、① = 1 × 400 = 400 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
先月までの兄の貯金額を ① とすると、弟は ② と表すことができる。よって、
① + 600：② – 200 = 5：3
5 × ( ② – 200 ) = 3 × ( ① + 600 )
① = 400
先月までの兄の貯金額は、① = 1 × 400 = 400 [円]

（４）A さんと B さんの所持金の比は 4：5 です。B さんが 900 円を使ったので、その比が 5：4 になりました。A さんの所持金はいくらですか。

答え（４）: 2000 円

解き方（４）: A さんと B さんの所持金の比の変化を線分図で表し、変化後の比の大きさをそろえると、

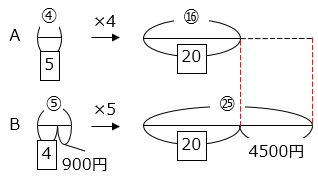
㉕ – ⑯ = 4500
① = 500
A さんの所持金は、④ = 4 × 500 = 2000 [円]

別の計算方法【内項の積 = 外項の積で求める方法】
A さんの所持金を ④ とすると、B さんのはじめの所持金は ⑤ と表すことができる。よって、
④：⑤ – 900 = 5：4
5 × ( ⑤ – 900 ) = 4 × ④
① = 500
Aさんの所持金は、④ = 4 × 500 = 2000 [円]