算数【基本】円とおうぎ形(角度・長さ・面積)
- 円とおうぎ形
- 【円】
●円の定義:円とは、ある点(円の中心)からの距離(半径)が等しい点の集まりである。
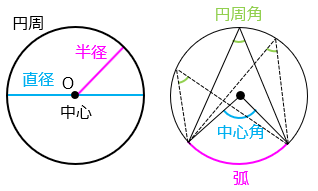
●円周率:円周が、直径の何倍になっているのかを表した数である。
3.1415926635… とどこまでも続く小数であることがわかっており、特に指定がなければ 3.14 を用いる。
●弧:円周の一部
●中心角:ある長さの弧と中心が作る角。中心角の大きさは弧の長さに比例する。
●円周角:ある長さの弧と、その弧を除いた円周上の 1 点で作られる角。1 つの弧に対する円周角の大きさは等しく、その弧に対する中心角の半分となる。
<円周の求め方>
円周 = 直径 × 円周率
<円の面積の求め方>
円の面積 = 半径 × 半径 × 円周率
<弧の長さの求め方>
弧
= 円周 × \(\dfrac{中心角}{360}\)
= 直径 × 円周率 × \(\dfrac{中心角}{360}\)
【おうぎ形】
●おうぎ形の定義:円を 2 つの半径で切り取った形
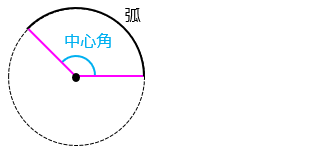
<おうぎ形の面積の求め方>
おうぎ形の面積
= 円の面積 × \(\dfrac{中心角}{360}\)
= 半径 × 半径 × 円周率 × \(\dfrac{中心角}{360}\)
円周率は3.14とします。
問1
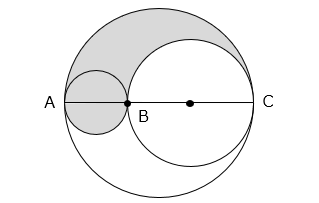
(1)図の 3 つの円において、AB = 10 cm、BC = 20 cm のとき、影の部分の周りの長さは何 cm ですか。
- 答え(1)
- 94.2 cm
- 解き方(1)
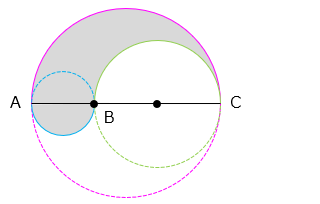
求めるのは 3 つの円の半円部分の弧の長さの和。
10 × 3.14 ÷ 2 + 20 × 3.14 ÷ 2 + 30 × 3.14 ÷ 2
= ( 10 + 20 + 30 ) × 3.14 ÷ 2 = 94.2 [cm]
(2)図の影の部分の面積は何 cm2 ですか。図に示した点は、各半円の中心とする。
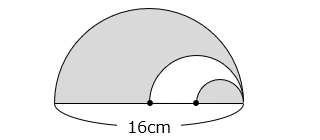
- 答え(2)
- 81.64 cm2
- 解き方(2)
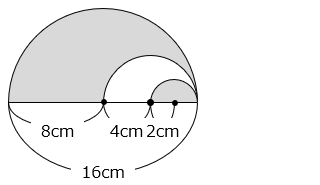
8 × 8 × 3.14 ÷ 2 – 4 × 4 × 3.14 ÷ 2 + 2 × 2 × 3.14 ÷ 2
= ( 64 – 16 + 4 ) × 3.14 ÷ 2 = 81.64 [cm2]
(3)半径が 8 cm の円の面積と、半径が 10 cm の円の半分の面積の差は何 cm2 ですか。
- 答え(3)
- 43.96 cm2
- 解き方(3)
- 半径 8 cm の円の面積は 8 × 8 × 3.14 = 64 × 3.14 [cm2]
半径 10 cm の円の半分の面積は 10 × 10 × 3.14 ÷ 2 = 50 × 3.14 [cm2]
よってその差は、
64 × 3.14 – 50 × 3.14
= ( 64 – 50 ) × 3.14 = 43.96 [cm2]
(4)図の影の部分の周りの長さは何 cm ですか。
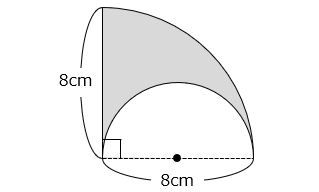
- 答え(4)
- 33.12 cm
- 解き方(4)

8 + ( 8 × 2 ) × 3.14 × \(\dfrac{90}{360}\) + 8 × 3.14 × \(\dfrac{180}{360}\)
= 8 + 16 × 3.14 × \(\dfrac{1}{4}\) + 8 × 3.14 × \(\dfrac{1}{2}\)
= 8 + 4 × 3.14 × 4 × 3.14
= 8 + 8 × 3.14 = 33.12 [cm]
(5)図は半径 2 cm と 3 cm の円です。影の部分の面積を求めなさい。
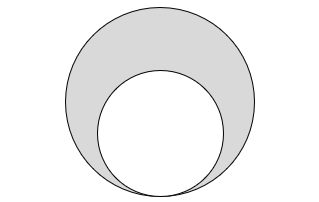
- 答え(5)
- 15.7 cm2
- 解き方(5)
- 3 × 3 × 3.14 – 2 × 2 × 3.14
= 9 × 3.14 – 4 × 3.14
= ( 9 – 4 ) × 3.14
= 5 × 3.14 = 15.7 [cm2]
(6)図のように、点 O を中心とする円周上に、円周の長さを 3 等分する 3 点 A、B、C があります。
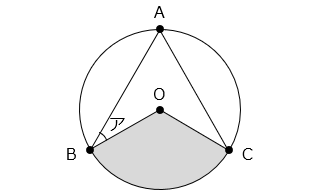
① 円の半径が 3 cm のとき、図の影の部分の面積は何 cm2 ですか。
- 答え(6)- ①
- 9.42 cm2
- 解き方(6)- ①
- 点 A、B、C は円周を 3 等分するので、影の部分の中心角は 120° である。
よって面積は、
3 × 3 × 3.14 × \(\dfrac{120}{360}\)
= 3 × 3.14 = 9.42 [cm2]
② 角アの大きさは何度ですか。
- 答え(6)- ②
- 30 度
- 解き方(6)- ②
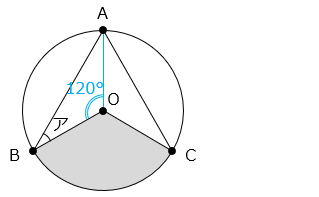
△AOB は角 AOB = 120° の 2 等辺三角形である。
よって角アの大きさは、
( 180 – 120 ) ÷ 2 = 30 [°]
(7)図のように、点 O、O’ を中心とする半径 3 cm の円が重なっています。このとき、影の部分の面積は何 cm2 ですか。
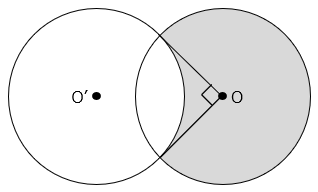
- 答え(7)
- 23.13 cm2
- 解き方(7)
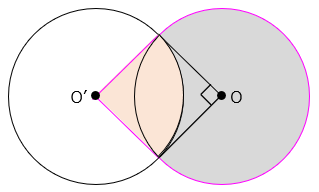
求める面積は \(\boxed{ }\) でかこまれた面積から、 のおうぎ形部分の面積を引けばよい。
3 × 3 + 3 × 3 × 3.14 × \(\dfrac{270}{360}\) – 3 × 3 × 3.14 × \(\dfrac{90}{360}\)
= 9 + 9 × 3.14 × ( \(\dfrac{3}{4}\) – \(\dfrac{1}{4}\) )
= 9 + 9 × 3.14 × \(\dfrac{1}{2}\) = 23.13 [cm2]
(8)図は点 O を中心とする半径 6 cm の円で、A、B、C、D、E、F、G、H は円周を 8 等分する点です。
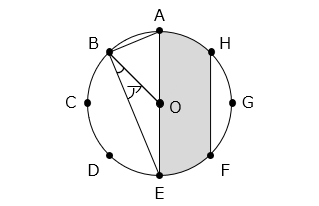
① 角アの大きさは何度ですか。
- 答え(8)- ①
- 22.5 度
- 解き方(8)- ①
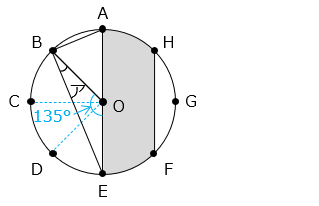
△BOE は二等辺三角形である。また、角 BOE は 360 × \(\dfrac{3}{8}\) = 135 [°] である。
よって、角アは、
( 180 – 135 ) ÷ 2 = 22.5 [°]
② 直線 AE と直線 FH と円周で囲まれる影の部分の面積は何 cm2 ですか。
- 答え(8)- ②
- 46.26 cm2
- 解き方(8)- ②
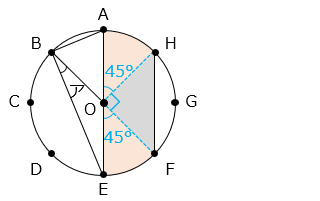
求める面積は、2 つの中心角 45° のおうぎ形と直角二等辺三角形の面積の和である。
6 × 6 × 3.14 × \(\dfrac{45}{360}\) × 2 + 6 × 6 × \(\dfrac{1}{2}\)
= 36 × 3.14 × \(\dfrac{1}{4}\) + 36 × \(\dfrac{1}{2}\)
= 9 × 3.14 + 18 = 46.26 [cm2]
(9)図の角アの大きさは何度ですか。
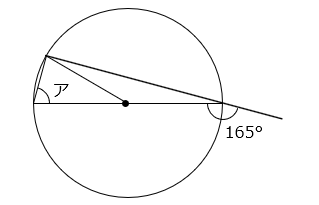
- 答え(9)
- 75 度
- 解き方(9)
- 【解1】円周角を利用する
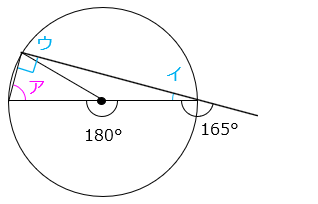
角イの大きさは 180 – 165 = 15 [°]
角ウは中心角 180° の円周角なので 90°。よって、
角ア = 180 – ( 90 + 15 ) = 75 [°]
【解2】二等辺三角形を利用する

角イの大きさは 180 – 165 = 15 [°]
△AOB は二等辺三角形より、
角ウ = 180 – 15 × 2 = 150 [°]
△BOC は二等辺三角形より、
角ア = 150 ÷ 2 = 75 [°]
(10)図のように円周を八等分した点をとったとき、影の部分の面積は何 cm2 ですか。
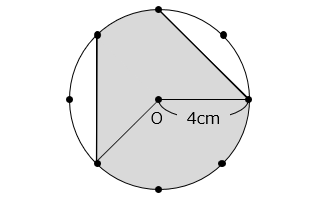
- 答え(10)
- 41.12 cm2
- 解き方(10)
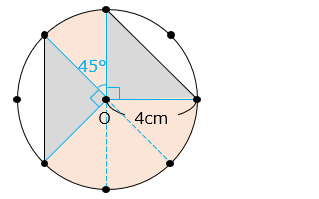
となり合った点と中心Oでできる中心角の大きさは 360 ÷ 8 = 45 [°]
図より、求める面積は、中心角 45° のおうぎ形4個と、2 つの直角二等辺三角形の和である。
4 × 4 × 3.14 × \(\dfrac{45\ ×\ 4}{360}\) + 4 × 4 ÷ 2 × 2
= 8 × 3.14 + 16
= 25.12 + 16 = 41.12 [cm2]
(11)図は、どちらも半径 6 cmのおうぎ形です。
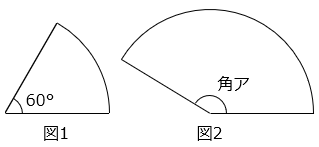
① 図1のおうぎ形の周りの長さは何 cm ですか。
- 答え(11)- ①
- 18.28 cm
- 解き方(11)- ①
- 6 × 2 × 3.14 × \(\dfrac{60}{360}\) + 6 × 2
= 6.28 + 12 = 18.28 [cm]
② 図2のおうぎ形の周りの長さは 27.7 cm でした。角アの大きさは何度ですか。
- 答え(11)- ②
- 150 度
- 解き方(11)- ②
- 図1の弧の長さは 6.28 cm
図2の弧の長さは 27.2 – 12 = 15.7 [cm]br>角度は弧の長さに比例するので、角アは、
60 × \(\dfrac{15.7}{6.28}\) = 60 × \(\dfrac{5}{2}\) = 150 [°]
問2
(1)図は半径 10 cm の円と、その中心を通る 5 本の直線です。影の部分の面積を求めなさい。
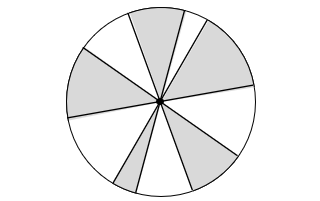
- 答え(1)
- 157 cm2
- 解き方(1)
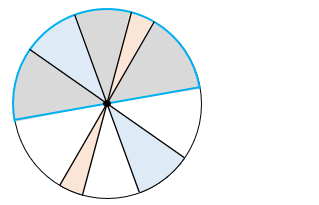
向かい合ったおうぎ形の面積は等しいので、求める面積は半円の面積と等しい。
10 × 10 × 3.14 ÷ 2 = 157 [cm2]
(2)おうぎ形を AB を折り目として折ったとき、O が円周上の点 C に重なりました。角アの大きさを求めなさい。
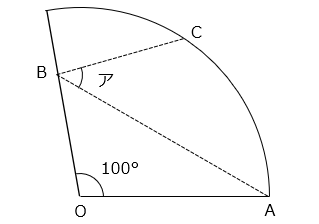
- 答え(2)
- 50 度
- 解き方(2)
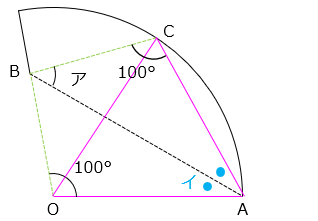
△AOB と △ACB は AB に対して対象の関係にある。したがって、角イ (●) の大きさは等しく、角 ACB は 100° である。
AO と AC と OC の長さは等しく、△OAC は正三角形になっている。
よって、角イは 60 ÷ 2 = 30 [°]、角アは、180 – ( 100 + 30 ) = 50 [°]である。
(3)図の影の部分の面積の合計は何 cm2 ですか。
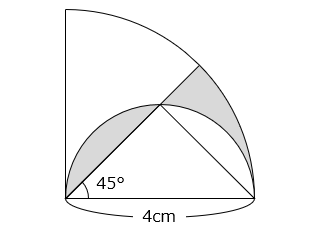
- 答え(3)
- 2.28 cm2
- 解き方(3)
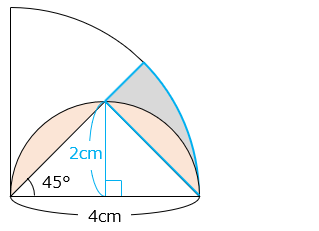
部分の面積は等しいので、求める面積は \(\boxed{ }\) 部分の面積と等しい。
4 × 4 × 3.14 × \(\dfrac{45}{360}\) – 4 × 2 ÷ 2
= 16 × 3.14 × \(\dfrac{1}{8}\) – 4
= 2 × 3.14 – 4 = 2.28 [cm2]
(4)図のような図形があります。
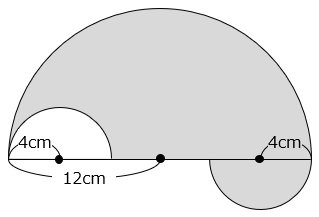
① 影の部分のまわりの長さを求めなさい。
- 答え(4)- ①
- 70.8 cm
- 解き方(4)- ①
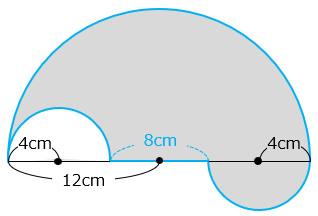
求める長さは、青線部分。
12 × 2 × 3.14 ÷ 2 + 4 × 2 × 3.14 + 8
= 12 × 3.14 + 8 × 3.14 + 8
= ( 12 + 8 ) × 3.14 + 8
= 62.8 + 8 = 70.8 [cm]
② 影の部分の面積を求めなさい。
- 答え(4)- ②
- 226.08 cm2
- 解き方(4)- ②
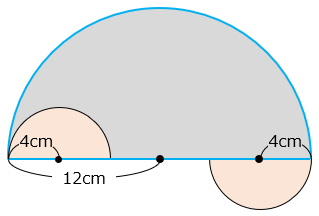
部分の面積は等しいので、求める面積は、半径 12 cm の半円の面積に等しい。
12 × 12 × 3.14 ÷ 2 = 226.08 [cm2]
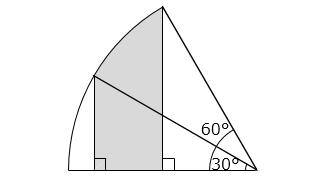
(5)図は、半径 6 cm、中心角 60° のおうぎ形です。影の部分の面積は何 cm2 ですか。
- 答え(5)
- 9.42 cm2
- 解き方(5)

△① と △② は、面積の等しい直角三角形である。よって、 部分の面積は等しく、求める面積は、中心角 30° のおうぎ形の面積に等しい。
6 × 6 × 3.14 × \(\dfrac{30}{360}\)
= 36 × 3.14 × \(\dfrac{1}{12}\)
= 3 × 3.14 = 9.42 [cm2]

































