算数【基本】円を含む図形
問1
正方形と半円とおうぎ形を組み合わせてできた図形の 部分の面積を求めなさい。ただし、円周率は3.14とします。
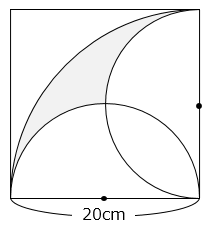
- 答え
- 57cm2
- 解き方
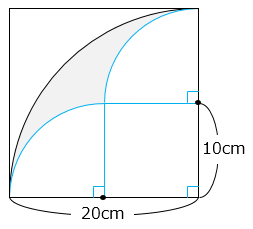
部分は、半径20cmのおうぎ形から、半径10cmのおうぎ形2つと1辺10cmの正方形を除いた図形である。よって、その面積は、
20 × 20 × 3.14 × \(\dfrac{90}{360}\) – ( 10 × 10 × 3.14 × \(\dfrac{90}{360}\) × 2 + 10 × 10 )
= 400 × 3.14 × \(\dfrac{1}{4}\) – { 100 × ( 6.28 × \(\dfrac{1}{4}\) + 1 ) }
= 314 – 257 = 57(cm2)
問2
長方形ABCDの辺AD上に点Oをとり、点Oを中心にしてコンパスで曲線をかきました。このとき、角アの大きさは何度ですか。
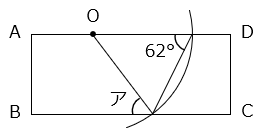
- 答え
- 56°
- 解き方
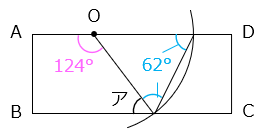
角ア = 180 – 124 = 56(°)
問3
1辺が1cmの正方形ABCDの周上に糸がたるむことなくまいてあります。図は、糸がたるまないようにA→B→C→Dの方向に1周分ほどいたときの糸の先端が動いた様子を太線で表しています。以下の問いに答えなさい。ただし、円周率は3.14とします。
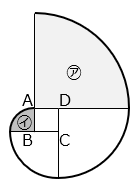
(1)図の太線の長さは何cmですか。
- 答え(1)
- 15.7cm
- 解き方(1)
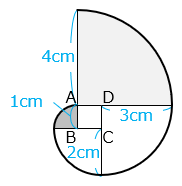
図より、
( 1 × 2 + 2 × 2 + 3 × 2 + 4 × 2 ) × 3.14 × \(\dfrac{1}{4}\)
= ( 2 + 4 + 6 + 8 ) × 3.14 × \(\dfrac{1}{4}\)
= 20 × 3.14 × \(\dfrac{1}{4}\) = 15.7(cm)
(2)㋐の面積は㋑の面積の何倍ですか。
- 答え(2)
- 16倍
- 解き方(2)
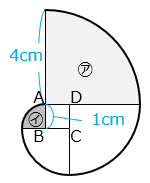
おうぎ形の面積は 半径 × 半径 × 円周率 × \(\dfrac{中心角}{360}\) で求めることができる。㋐と㋑は中心角が等しいので、半径の倍数 × 半径の倍数が面積の倍数となる。㋑の半径は㋐の半径の4倍である。
よって面積は、4 × 4 = 16(倍)となる。
(3)2周分の糸をほどいたとき、2周目で糸が通った部分の面積は何cm2ですか。
- 答え(3)
- 136.59cm2
- 解き方(3)
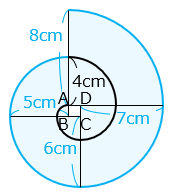
( 5 × 5 + 6 × 6 + 7 × 7 + 8 × 8 ) × 3.14 × \(\dfrac{1}{4}\)
= ( 25 + 36 + 49 + 64 ) × 3.14 × \(\dfrac{1}{4}\)
= 174 × 3.14 × \(\dfrac{1}{4}\)
= \(\dfrac{87}{2}\) × 3.14
= 87 × 1.57 = 136.59(cm2)
問4
図は、円と正方形を組み合わせたものです。円の直径が10cmのとき、 部分の面積を求めなさい。ただし、円周率は3.14とします。
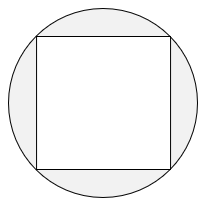
- 答え
- 28.5cm2
- 解き方
- 【解き方①】正方形はひし形の一種と考えて面積を求める
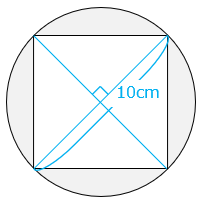
ひし形の面積は 対角線 × 対角線 ÷ 2 で求められるので、正方形の面積は、
10 × 10 ÷ 2 = 50(cm2)
よって求める面積は、
5 × 5 × 3.14 – 50 = 28.5(cm2)
【解き方②】正方形を三角形の組み合わせとして面積を求める
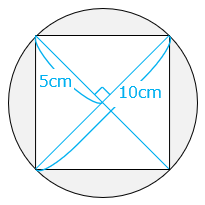
正方形の面積は、
10 × 5 × \(\dfrac{1}{2}\) × 2 = 50(cm2)
5 × 5 × 3.14 – 50 = 28.5(cm2)
問5
図は、円を4等分してできるおうぎ形で、点C、Dはその円周をさらに3等分する点です。以下の問いに答えなさい。ただし、円周率は3.14とします。
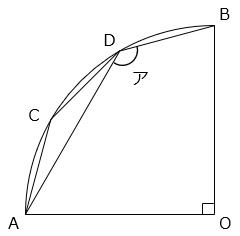
(1)角アの大きさは何度ですか。
- 答え(1)
- 135°
- 解き方(1)
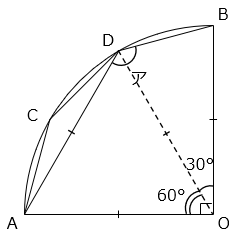
円周角は弧の長さに比例するので、角AOD = 60°、角BOD = 30° である。
△OADは正三角形なので、角ADO = 60°
△OBDは OB = OD の二等辺三角形なので、
角BDO = ( 180 – 30 ) ÷ 2 = 75°
角ア
= 角ADO + 角BDO
= 60 + 75 = 135(°)
(2)ACの長さが6cmのとき、三角形ACDの面積は何cm2ですか。
- 答え(2)
- 9cm2
- 解き方(2)
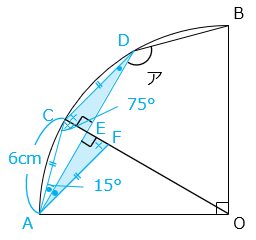
ADとOCの交点をEとし、点AからCDに平行な直線を伸ばしたときのOCとの交点をFとする。△DCEと△AFEは合同な三角形となるため面積は等しくなる。したがって、求める△ACDの面積は△ACFの面積に等しい。
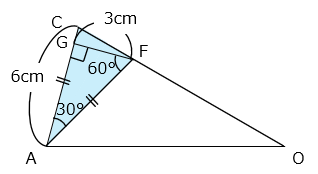
△ACFは頂角Aが30℃の二等辺三角形である。点FからACに垂直な直線をおろしたときの交点をGとすると、△AFGは底角が30°と60°の直角三角形となる。よって、
FG = AF ÷ 2 = 6 ÷ 2 = 3(cm)
△ACD
= △ACF
= 6 × 3 ÷ 2 = 9(cm2)
問6
図の 部分の面積を求めなさい。ただし、点Oは円の中心とし、円周率は3.14とします。
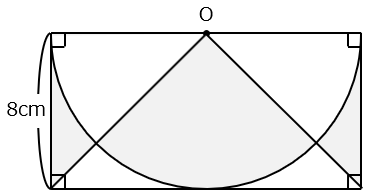
- 答え
- 64cm2
- 解き方
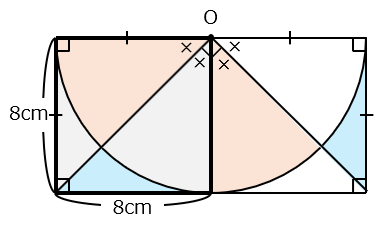
求める面積は太線で囲まれた正方形の面積に等しいので、
8 × 8 = 64(cm2)
問7
図の 部分の面積を求めなさい。ただし、円周率は3.14とします。
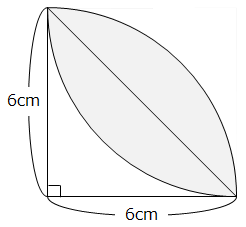
- 答え
- 20.52cm2
- 解き方
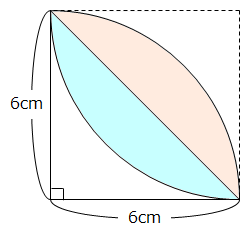
部分と 部分の面積は等しいので、
( 6 × 6 × 3.14 × \(\dfrac{1}{4}\) – 6 × 6 × \(\dfrac{1}{2}\) ) × 2
= ( 28.26 – 18 ) × 2
= 10.26 × 2 = 20.52(cm2)
問8
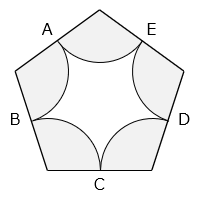
図は1辺が20cmの正五角形です。各辺の真ん中の点を A、B、C、D、E とするとき、 部分の面積を求めなさい。ただし、円周率は3.14とします。
- 答え
- 471cm2
- 解き方
- 五角形の内角の和は ( 5 – 2 ) × 180 = 540(°)より、各おうぎ形の中心角の和は540°、また各おうぎ形の半径は10cmである。
よって、求める面積は、
10 × 10 × 3.14 × \(\dfrac{540}{360}\)
= 314 × \(\dfrac{3}{2}\) = 471(cm2)
問9
図は、1辺の長さが12cmの正方形と半径6cmの半円を組み合わせたものです。 部分の面積を求めなさい。ただし、円周率は3.14とします。
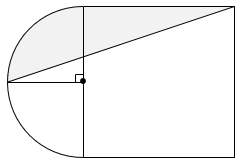
- 答え
- 46.26cm2
- 解き方
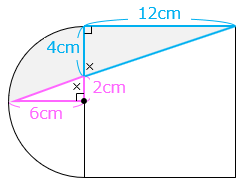
△と△は互いに相似な三角形で、相似比は 2:1、面積比は 4:1 である。
△ = 12 × 4 ÷ 2 = 24(cm2)
△ = \(\dfrac{1}{4}\) × △
= \(\dfrac{1}{4}\) × 24 = 6(cm2)
求める面積は、
6 × 6 × 3.14 × \(\dfrac{1}{4}\) – 6 + 24
= 28.26 – 6 + 24 = 46.26(cm2)
問10
図は、1辺の長さが6cmの正方形と4分の1の円です。このとき、 部分の面積を求めなさい。ただし、円周率は3.14とします。
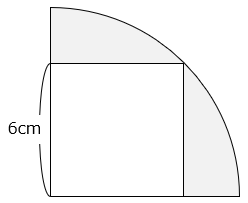
- 答え
- 20.52cm2
- 解き方
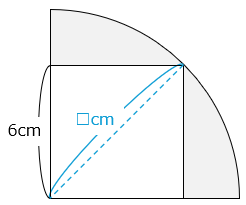
正方形の面積は 6 × 6 = 36(cm2)
正方形の対角線(4分の1の円の半径)を□cmとすると、
正方形の面積
= □ × □ ÷ 2 = 36
□ × □ = 72
求める面積は、
□ × □ × 3.14 × \(\dfrac{1}{4}\) – 36
= 72 × 3.14 × \(\dfrac{1}{4}\) – 36
= 18 × 3.14 – 36 = 20.52(cm2)
問11
図は、長方形と半円を組み合わせ、長方形の対角線を1本引いた図です。このとき、 部分と 部分の面積の差を求めなさい。ただし、円周率は3.14とします。
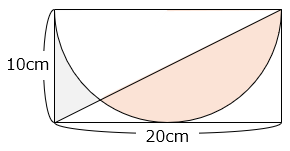
- 答え
- 57cm2
- 解き方
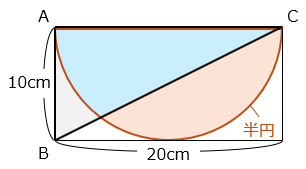
部分と の面積は、それぞれ△ABCと半円から 部分の面積を引いた部分である。
よって、求める面積の差は△ABCと半円の面積の差に等しい。
△ABC = 10 × 20 ÷ 2 = 100(cm2)
半円 = 10 × 10 × 3.14 ÷ 2 = 157(cm2)
面積の差は、157 – 100 = 57(cm2)
問12
図のように、円を4等分したおうぎ形を並べて正方形をつくりました。正方形の対角線の長さが4cmのとき、 部分の面積を求めなさい。ただし、円周率は3.14とします。
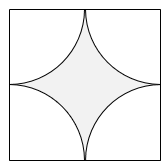
- 答え
- 1.72cm2
- 解き方
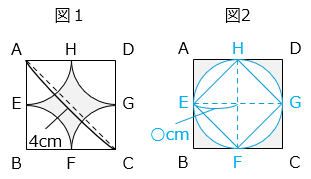
図1と図2の 部分の面積は等しい。
また、□EFGHの面積は□ABCDの \(\dfrac{1}{2}\) である。
□ABCD = 4 × 4 ÷ 2 = 8(cm2)
□EFGH = 8 ÷ 2 = 4(cm2)
図2の円の半径を○cmとすると、
□EFGH
= 2 × ○ × 2 × ○ ÷ 2 = 4
2 × ○ × ○ = 4
○ × ○ = 2
求める面積は、
8 – ○ × ○ × 3.14
= 8 – 2 × 3.14 = 1.72(cm2)
問13
図は1辺の長さが6cmの正方形の中に、ABを半径とする円の一部をかき、点Bと点Pを直線で結んだものです。以下の問いに答えなさい。ただし、円周率は3.14とします。
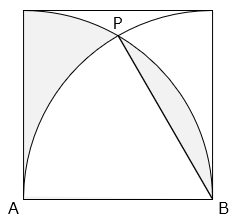
(1) 部分の面積は何cm2ですか。
- 答え(1)
- 9.42cm2
- 解き方(1)
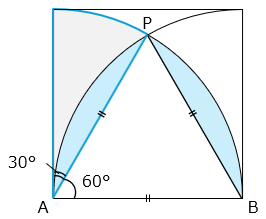
△APBは正三角形であり、 の面積は互いに等しい。
よって求める面積は、青線で囲まれたおうぎ形の面積となる。
6 × 6 × 3.14 × \(\dfrac{30}{360}\)
= 36 × 3.14 × \(\dfrac{1}{12}\)= 3 × 3.14 = 9.42(cm2)
(2) 部分のまわりの長さは何cmですか。
- 答え(2)
- 27.7cm
- 解き方(2)
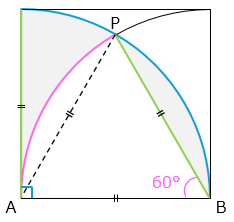
6 × 2 × 3.14 × \(\dfrac{90}{360}\) + 6 × 2 × 3.14 × \(\dfrac{60}{360}\) + 6 × 2
= 3 × 3.14 + 2 × 3.14 + 12 = 27.7(cm)
問14
図のように、直角三角形の中に円が入っています。 部分の面積が91.74cm2のとき、円の半径は何cmですか。ただし、円周率は3.14とします。
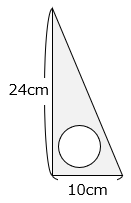
- 答え
- 3cm
- 解き方
- 円の面積は、
10 × 24 ÷ 2 – 91.74
= 120 – 91.74 = 28.26(cm2)
円の半径を□cmとすると、
□ × □ × 3.14 = 28.26
□ × □ = 28.26 ÷ 3.14 = 9
□ = 3(cm)
問15
図は、1辺が20cmの正方形の内側に4つの円がくっついています。 部分の面積を求めなさい。ただし、円周率は3.14とします。
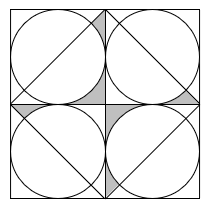
- 答え
- 21.5cm2
- 解き方
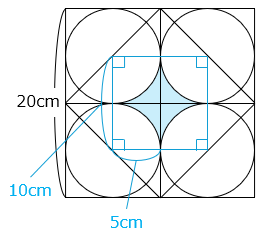
部分の面積は、 部分の面積に等しい。
よって求める面積は、
10 × 10 – 5 × 5 × 3.14 × \(\dfrac{90\ ×\ 4}{360}\)
= 100 – 78.5 = 21.5(cm2)


































