- 三角形の合同条件
- 2つの図形を、回転したり、移動したり、裏返したりすることで、ぴったりと重ねることができるとき、この2つの図形は「合同」という
【三角形の合同条件】
①~③の条件のうち、どれか1つを満たしているとき、三角形㋐と㋑は合同といえる。
① 3つの辺の長さがそれぞれ等しい。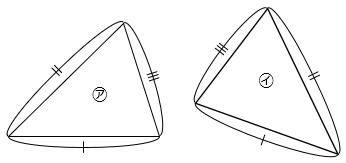
② 2つの辺の長さと、その間の角の大きさが等しい。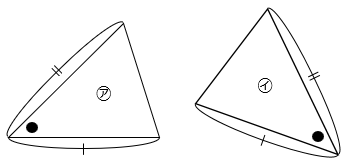
③ 1つの辺の長さと、その両端の角の大きさがそれぞれ等しい。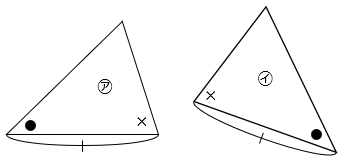
- 相似
- 形は同じで、大きさが異なる図形どうしを、互いに「相似」という。相似な図形では、対応する角および対応する辺の比(相似比)はそれぞれ等しい。
【三角形の相似条件】
①~③の条件のうち、どれか1つを満たしているとき、三角形㋐と㋑は相似といえる。
① 2組の角の大きさがそれぞれ等しい。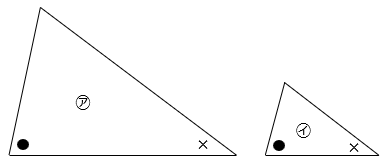
② 3組の辺の比がそれぞれ等しい。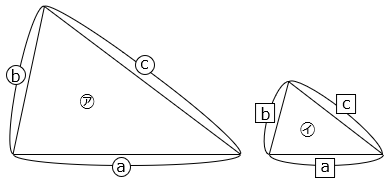
③ 2組の辺の比が等しく、その間の角の大きさが等しい。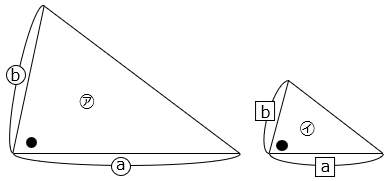
【平行線と相似】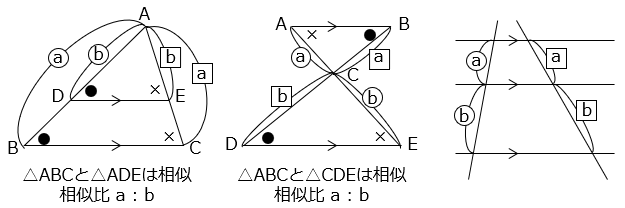
【面積比と相似】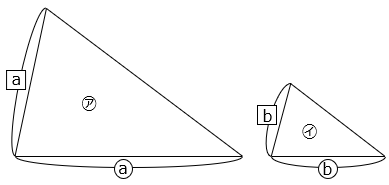
三角形㋐と㋑が相似で、相似比が a:b のとき、面積比は「三角形㋐:三角形㋑ = a × a:b × b」となる。
問1
直角二等辺三角形ABCと正方形DEFGが重なっています。点Oは、正方形DEFGの対角線の交点で、辺BC上にあります。正方形DEFGの面積が80cm2、辺ABの長さが12cmのとき、 部分の面積を求めなさい。
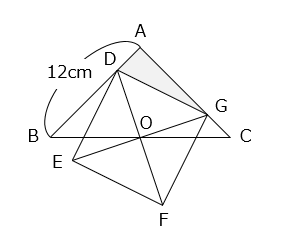
- 答え
- 16cm2
- 解き方
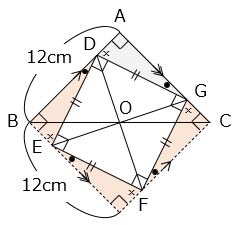
色のついた三角形 (
(1つの辺の長さと、その両端の角の大きさがそれぞれ等しい)
よって、求める面積は、
( 12 × 12 – 80 ) ÷ 4 = 16(cm2)
問2
(1)△ABCの面積は54cm2です。 部分の面積を求めなさい。ただし、同じ記号は等しい長さを表します。
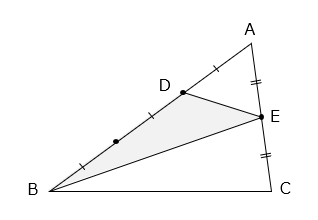
- 答え(1)
- 18cm2
- 解き方(1)
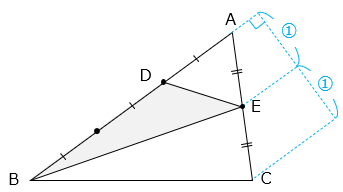
△DBEと△ABCは、底辺の比が 2:3、高さの比が 1:2 より、
△DBE
= △ABC × \(\dfrac{2}{3}\) × \(\dfrac{1}{2}\)
= 54 × \(\dfrac{1}{3}\) = 18(cm2)
(2)三角形ABCの面積は210cm2です。また、辺ABを3等分、辺BCを2等分し、図のように点D、Eをとりました。このとき、三角形DBEの面積を求めなさい。
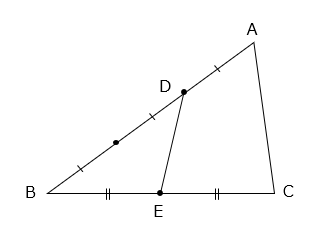
- 答え(2)
- 70cm2
- 解き方(2)
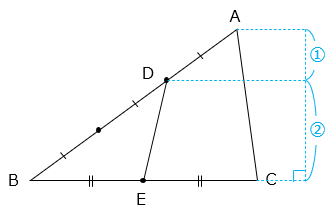
△DBEと△ABCは、底辺の比が 1:2、高さの比が 2:3 より、
△DBE
= △ABC × \(\dfrac{1}{2}\) × \(\dfrac{2}{3}\)
= 210 × \(\dfrac{1}{3}\) = 70(cm2)
【補助線DCを引いて考えてみると】
△DBC = 210 × \(\dfrac{2}{3}\) = 140
△DBE = 140 × \(\dfrac{1}{2}\) = 70(cm2)
(3)面積が96cm2の平行四辺形ABCDに、図のように点E、Fをとりました。 部分の面積を求めなさい。
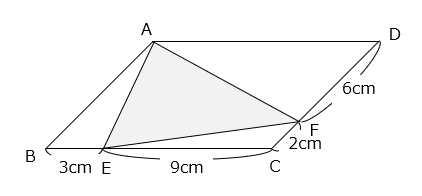
- 答え(3)
- 39cm2
- 解き方(3)
- 補助線ACを引く
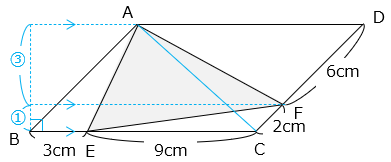
△ABEと△AECは高さが等しく、底辺の比が 1:3 より、
△ABE
= △ABC × \(\dfrac{1}{4}\)
= □ABCD × \(\dfrac{1}{2}\) × \(\dfrac{1}{4}\)
= 96 × \(\dfrac{1}{8}\) = 12(cm2)
△ADFと△AFCは高さが等しく、底辺の比が 3:1 より、
△ADF
= △ADC × \(\dfrac{3}{4}\)
= □ABCD × \(\dfrac{1}{2}\) × \(\dfrac{3}{4}\)
= 96 × \(\dfrac{3}{8}\) = 36(cm2)
△CEFと△ABEは、高さの比が 1:4 (CF:CD)、底辺の比が 3:1 (EC:BE) より、
△CEF
= △ABE × \(\dfrac{1}{4}\) × 3
= 12 × \(\dfrac{3}{4}\) = 9(cm2)
求める面積は、
□ABCD – ( △ABE + △ADF + △CEF)
= 96 – ( 12 + 36 + 9 ) = 39(cm2)
問3
(1)辺AFの長さを求めなさい。
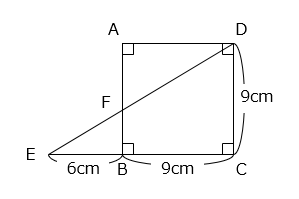
- 答え(1)
- 5.4cm ( \(5\dfrac{2}{5}\) cm)
- 解き方(1)
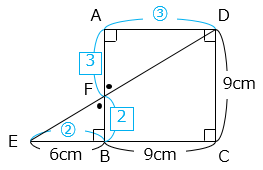
△ADFと△BEFは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AD:BE = 3:2 である。
よって、
AF = 9 × \(\dfrac{3}{5}\) = 5.4(cm)
(2)辺BEと辺ECの長さの比は 4:3 で、三角形DBCの面積は42cm2です。
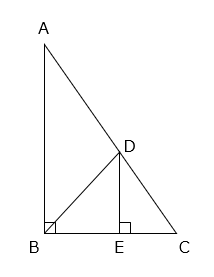
① 三角形DCEの面積を求めなさい。
- 答え(2)- ①
- 18cm2
- 解き方(2)- ①
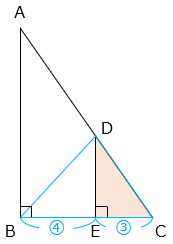
△DCEと△DBCは、高さが等しく、底辺の比が 3:7 なので、
△DCE
= △DBC × \(\dfrac{3}{7}\)
= 42 × \(\dfrac{3}{7}\) = 18(cm2)
② 三角形ABCの面積を求めなさい。
- 答え(2)- ②
- 98cm2
- 解き方(2)- ②
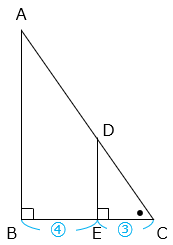
△DCEと△ABCは相似(2組の角の大きさがそれぞれ等しい)で、相似比は CE:CB = 3:7 より、面積比は 9:49 となる。
△ABC
= △DCE × \(\dfrac{49}{9}\)
= 18 × \(\dfrac{49}{9}\) = 98(cm2)
(3)長方形ABCDの辺AD上に点E、辺BE上に点Fがあります。辺ABの長さを求めなさい。
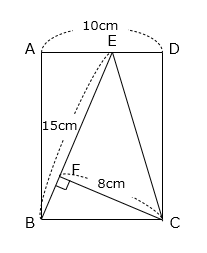
- 答え(3)
- 12cm
- 解き方(3)
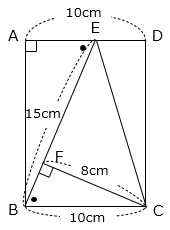
△ABEと△FCBは相似(2組の角の大きさがそれぞれ等しい)で、相似比は BE:BC = 3:2 である。
AB
= CF × \(\dfrac{3}{2}\)
= 8 × \(\dfrac{3}{2}\) = 12(cm)
(4) 部分の面積を求めなさい。
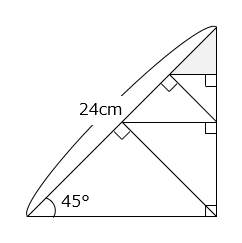
- 答え(4)
- 4.5cm2
- 解き方(4)
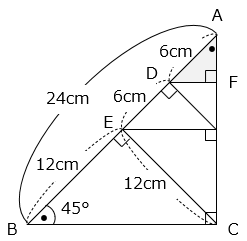
△ABCは直角二等辺三角形であり、直角を頂点として、底辺に垂直に直線を引くと、交わる点は底辺を2等分する。
△ABCと△ADFは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AB:AD = 4:1 なので、面積比は 16:1 となる。
△ABCと△BCEも相似で、△BCEは BE = CE の直角二等辺三角形となる。
△ADF
= △ABC × \(\dfrac{1}{16}\)
= 24 × 12 ÷ 2 × \(\dfrac{1}{16}\)
= 144 × \(\dfrac{1}{16}\) = 9(cm2)
(5)図のような長方形ABCDがあります。三角形ADFの面積を求めなさい。
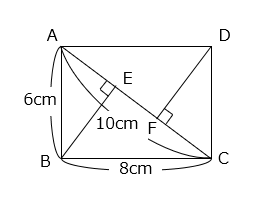
- 答え(5)
- 15.36cm2
- 解き方(5)
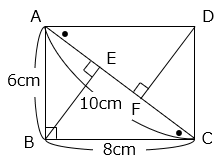
△ABCと△ADFは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AC:AD = 5:4 なので、面積比は 25:16 となる。
△ADF
= △ABC × \(\dfrac{16}{25}\)
= 8 × 6 ÷ 2 × \(\dfrac{16}{25}\)
= 24 × \(\dfrac{16}{25}\) = 15.36(cm2)
(6)三角形ABCを拡大すると三角形DEFになりました。このとき、辺DFの長さを求めなさい。ただし、角A = 角D、角B = 角Eとします。
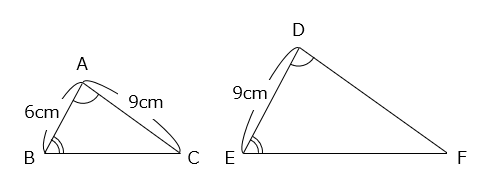
- 答え(6)
- 13.5cm
- 解き方(6)
- △ABCと△DEFは相似で、相似比は AB:DE = 2:3 である。
よって、
DF = AC × \(\dfrac{3}{2}\) = 9 × \(\dfrac{3}{2}\) = 13.5(cm)
(7)図の直角三角形において、ADの長さを求めなさい。
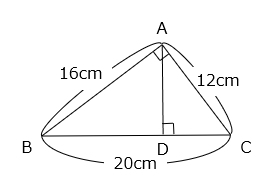
- 答え(7)
- 9.6cm
- 解き方(7)
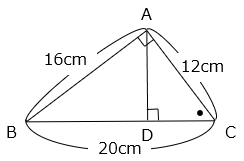
△ABCと△ADCは相似(2組の角の大きさがそれぞれ等しい)で、相似比は BC:AC = 5:3 である。
よって、
AD = AB × \(\dfrac{3}{5}\) = 16 × \(\dfrac{3}{5}\) = 9.6(cm)
問4
(1)長方形ABCDで、BE:EC = 3:2 です。三角形FECの面積が4cm2のとき、長方形ABCDの面積を求めなさい。
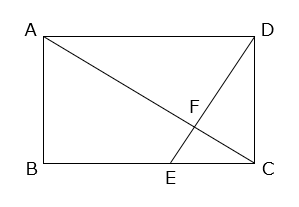
- 答え(1)
- 70cm2
- 解き方(1)
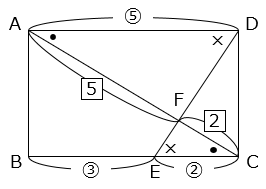
△FECと△FADは相似(2組の角の大きさがそれぞれ等しい)で、相似比は CE:AD = 2:5 より、面積比は 4:25 となる。
よって、
△FAD
= △FEC × \(\dfrac{25}{4}\)
= 4 × \(\dfrac{25}{4}\) = 25(cm2)
また、AF:FC = 5:2 より、
△FCD
= △FAD × \(\dfrac{2}{5}\)
= 25 × \(\dfrac{2}{5}\) = 10(cm2)
よって、
□ABCD
= 2 × △ACD
= 2 × ( 25 + 10 ) = 70(cm2)
(2)平行四辺形ABCDと三角形BCEの面積の比を、最も簡単な整数の比で表しなさい。ただし、CF:FD = 2:1 とします。
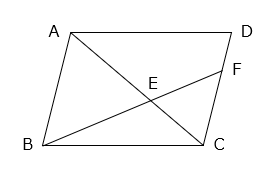
- 答え(2)
- 5:1
- 解き方(2)
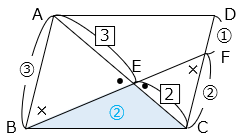
△ABEと△CFEは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AB:CF = 3:2 となる。
よって、AE:EC = 3:2 となる。
△BCEの面積を②とすると、△ABC = ② × \(\dfrac{5}{2}\) = ⑤ と表すことができる。
□ABCD
= △ABC × 2 = ⑤ × 2 = ⑩ より、
□ABCD:△BCE = ⑩:② = 5:1
(3)合同な平行四辺形ABCDとEFBGを重ね合わせました。対角線ACと対角線FGの交点を点P、対角線ACと辺BGの交点を点Qとし、AE = 6cm、FB = 12cm、AC = 35cm です。
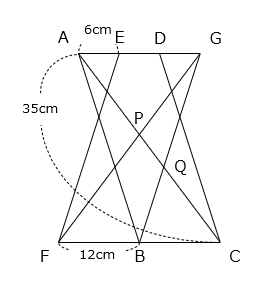
① APの長さを求めなさい。
- 答え(3)- ①
- 15cm
- 解き方(3)- ①
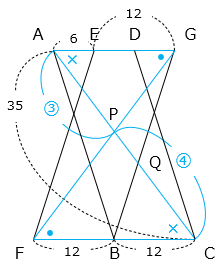
△APGと△CPFは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AG:CF = 3:4 となる。
よって、AP:PC = 3:4 より、
AP = 35 × \(\dfrac{3}{7}\) = 15(cm)
② 三角形AQGの面積は三角形PQGの面積の何倍ですか。
- 答え(3)- ②
- 3.5倍
- 解き方(3)- ②
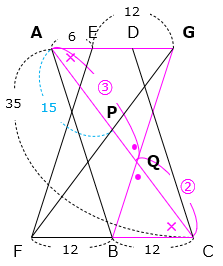
△AQGと△BQCは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AG:BC = 3:2 となる。
よって、AQ:QC = 3:2 より、
AQ = 35 × \(\dfrac{3}{5}\) = 21(cm)
PQ = 21 – 15 = 6(cm)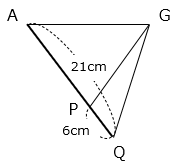
△AQGと△PQGは高さが等しく、底辺の比が AQ:PQ = 21:6 より、面積比は 21:6 となるので、
21 ÷ 6 = 3.5(倍)
(4)面積が36cm2の平行四辺形ABCDがあります。点Eは辺BCの真ん中の点です。このとき、 部分の面積を求めなさい。
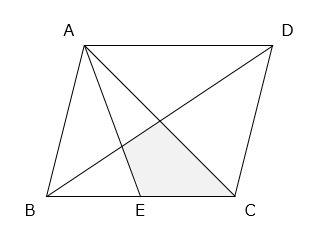
- 答え(4)
- 6cm2
- 解き方(4)
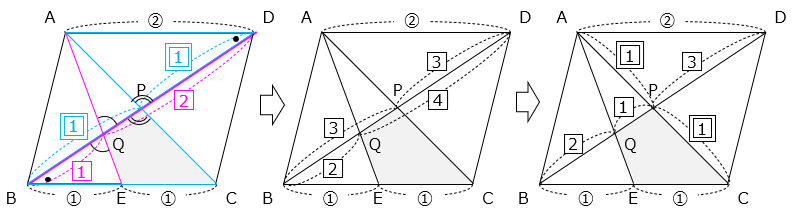
BDとACの交点をP、BDとAEの交点をQとする。
△APDと△BPCは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AD:BC = 1:1 より、BP:PD = 1:1。
△AQDと△BQEは相似(2組の角の大きさがそれぞれ等しい)で、相似比は AD:BE = 2:1 より、BQ:QD = 1:2。
比の大きさをそろえると、BQ:QP:PD = 2:1:3 となる。
△BPC
= △ABC × \(\dfrac{1}{2}\)
= □ABCD × \(\dfrac{1}{2}\) × \(\dfrac{1}{2}\)
= 36 × \(\dfrac{1}{4}\) = 9(cm2)
△BPCと△BQEは、底辺の比が 2:1、高さの比が 3:2 より、
△BQE
= △BPC × \(\dfrac{1}{2}\) × \(\dfrac{2}{3}\)
= 9 × \(\dfrac{1}{3}\) = 3(cm2)
求める面積は、
△BPC – △BQE = 9 – 3 = 6(cm2)
