算数【基本】数の範囲と概数
問1
数の範囲を表す言葉について、□ に当てはまる言葉を㋐、㋑から選びなさい。
㋐ ふくまれる ㋑ ふくまれない
(1)「5より大きい」数に、5は \(\boxed{ }\)。
- 答え(1)
- ㋑
(2)「5以上」の数に、5は \(\boxed{ }\)。
- 答え(2)
- ㋐
(3)「5未満」の数に、5は \(\boxed{ }\)。
- 答え(3)
- ㋑
(4)「5以下」の数に、5は \(\boxed{ }\)。
- 答え(4)
- ㋐
問2
\(\boxed{ }\) に当てはまる数、または言葉を答えなさい。
(1)「15以上20未満」の数で、最も小さい整数は \(\boxed{①}\)、最も大きい整数は \(\boxed{②}\) です。
- 答え(1)
- ①:15 ②:19
(2)㋐~㋓に示した範囲の中で、121が含まれているのは \(\boxed{ }\) です。すべて答えなさい。
㋐ 120より大きく121以下
㋑ 120以上121未満
㋒ 121より大きく122未満
㋓ 120以上121以下
- 答え(2)
- ㋐、㋓
(3)3.9や3.99、3.999999などは \(\boxed{ }\) 未満の数です。 \(\boxed{ }\) に当てはまる最も小さい整数を答えなさい。
- 答え(3)
- 4
問3
共通の範囲について、\(\boxed{ }\) に当てはまる数、または言葉を答えなさい。
(1)8以上15以下と、10以上15以下の共通の範囲は、\(\boxed{①}\) 以上 \(\boxed{②}\) 以下です。
- 答え(1)
- ①:10 ②:15
(2)20以上50未満と、35以上80未満の共通の範囲は、\(\boxed{①}\) 以上 \(\boxed{②}\) 未満です。
- 答え(2)
- ①:35 ②:50
(3)10と200の間と、25から300までの共通の範囲は、25 \(\boxed{①}\) 200 \(\boxed{②}\) です。
- 答え(3)
- ①:以上 ②:未満
問4
1428の概数について、\(\boxed{ }\) に当てはまる数、または言葉を答えなさい。
- ヒント
- ※切り捨て:求める位未満の数をすべて0とみなします
※切り上げ:求める位未満の数が0よりも大きければ、求める位の数を1大きくします
※四捨五入:求める位の1つ下の位の数字が0、1、2、3、4のときは切り捨てて、5、6、7、8、9のときは切り上げます
概数とは、およその数のことです
(1)1428を切り捨てて、百の位までの概数で表すと \(\boxed{①}\)、十の位までの概数で表すと \(\boxed{②}\) です。
- 答え(1)
- ①:1400 ②:1420
(2)1428を切り上げて、百の位までの概数で表すと \(\boxed{①}\)、十の位までの概数で表すと \(\boxed{②}\) です。
- 答え(2)
- ①:1500 ②:1430
(3)1428を四捨五入して、百の位までの概数で表すと \(\boxed{①}\)、十の位までの概数で表すと \(\boxed{②}\) です。
- 答え(3)
- ①:1400 ②:1430
問5
(1)7821を切り捨てて、千の位まで概数にしなさい。
- ヒント(1)
- 百の位以下を0にする。
- 答え(1)
- 7000
(2)6990002を切り上げて、一万の位までの概数にしなさい。
- ヒント(2)
- 千の位以下は0ではないので10000とみなす。
- 答え(2)
- 7000000
(3)304613を四捨五入して、上から2けたの概数にしなさい。
- ヒント(3)
- 上から3桁目、つまり千の位を四捨五入する。
- 答え(3)
- 300000
問6
小数5.1708を四捨五入し、概数を求めます。
(1)小数第1位までの概数にしなさい。
- ヒント(1)
- 小数第2位を四捨五入する
- 答え(1)
- 5.2
(2)小数第3位までの概数にしなさい。
- ヒント(2)
- 小数第4位を四捨五入する
- 答え(2)
- 5.171
(3)小数第3位以下を四捨五入しなさい。
- ヒント(3)
- 小数第3位を四捨五入する
- 答え(3)
- 5.17
(4)小数第3位未満を四捨五入しなさい。
- ヒント(4)
- 小数第4位を四捨五入する
- 答え(4)
- 5.171
問7
ある数を千の位までの概数にしたところ、7000になりました。ある数の範囲について \(\boxed{ }\) に当てはまる数や言葉を答えなさい。
(1)切り捨ての場合 \(\boxed{①}\) 以上8000 \(\boxed{②}\)
数の範囲を答えなさい。
- 答え(1)
- ①:7000 ②:未満
(2)切り上げの場合 \(\boxed{①}\) より大きく7000 \(\boxed{②}\)
- 答え(2)
- ①:6000 ②:以下
(3)四捨五入の場合 \(\boxed{①}\) 以上7500 \(\boxed{②}\)
- 答え(3)
- ①:6500 ②:未満
問8
数の範囲を答えなさい。
(1)切り上げて、百の位までの概数であらわすと36200になります。
- 答え(1)
- 36100より大きく36200以下
(2)切り捨てて、百の位までの概数であらわすと3300になります。
- 答え(2)
- 3300以上3400未満
(3)十の位を四捨五入して概数であらわすと1500になります。
- 答え(3)
- 1450以上1550未満
(4)四捨五入して、小数第1位までの概数であらわすと1.7になります。
- 答え(4)
- 1.65以上1.75未満
問9
図のような数直線があります。四捨五入して小数第1位までの概数にすると4.5になるのは、①~⑤のうちどれですか。すべて答えなさい。

- ヒント
- 四捨五入して小数第1位までの概数にすると、4.5になるのは4.45以上4.55未満の数
- 答え
- ②、③、④
問10
ある数Aは、22以上25未満の数です。また、ある数Bは28以上30以下の数です。
- ヒント
- A、Bの範囲を図で表すと、
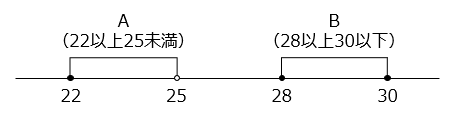
(●値を含む、○値を含まない)
※●と●の計算値 ⇒ 範囲に含まれる
※●と○の計算値 ⇒ 範囲に含まれない
※○と○の計算値 ⇒ 範囲に含まれない
(1)A + Bの値がふくまれる範囲を答えなさい。
- 答え(1)
- 50以上55未満
(2)B – Aの値がふくまれる範囲を答えなさい。
- 答え(2)
- 3より大きく8以下
(3)A × Bの値がふくまれる範囲を答えなさい。
- 答え(3)
- 616以上750未満


