算数【基本】速さ・時間・道のり

問１

（１）分速 70 m で 30 分間歩きました。歩いた距離は何 kmですか。

答え（１）: 2.1 km

解き方（１）: 70 × 30 = 2100 [m] = 2.1 [km]

（２）870 ｍの道のりを、分速 60 m で歩きました。何分何秒かかりましたか。

答え（２）: 14 分 30 秒

解き方（２）: 870 ÷ 60 = 14.5 [分] = 14 分 30 秒

（３）分速 50 mで 8 kmの道のりを歩くと、何時間何分かかりますか。

答え（３）: 2 時間 40 分

解き方（３）: 8 × 1000 ÷ 50 = 160 [分] = 2 時間 40 分

（４）A 地点と B 地点の間を、行きは時速 5 km、帰りは時速 4 km で歩いたので、往復で 9 時間かかりました。A 地点と B 地点は何 kmはなれていますか。

答え（４）: 20 km

解き方（４）: A地点とB地点の間の距離を □ km とすると、
\(\dfrac{□}{5}\) + \(\dfrac{□}{4}\) = 9
□ × ( \(\dfrac{1}{5}\) + \(\dfrac{1}{4}\) ) = 9
□ × \(\dfrac{9}{20}\) = 9
□ = 20 [km]

（５）280 km はなれた A 駅と B 駅の間を、行きは時速 140 km の電車に乗り、帰りは時速 70 km の電車に乗って往復しました。往復するのにかかった時間は何時間ですか。

答え（５）: 6 時間

解き方（５）: \(\dfrac{280}{140}\) + \(\dfrac{280}{70}\) = 6 [時間]

問２

（１）時速 40 kmで走る車が 100 m進むのにかかる時間は何秒ですか。

答え（１）: 9 秒

解き方（１）: 時速 40 km を秒速 □m に変換すると、
( 40 × 1000 ) ÷ ( 60 × 60 ) = 秒速 \(\dfrac{100}{9}\) m となる。
100 ÷ \(\dfrac{100}{9}\) = 9 [秒]

【別解】
速さが一定のとき、時間と距離は比例する。
100 m 進むのにかかる時間を □ 秒とすると、
1 × 60 × 60：40 × 1000 = □：100
9：100 = □：100
□ = 9 [秒]

（２）分速 60 m で歩くと 15 分かかる道を、分速 90 m の速さで走ると何分かかりますか。

答え（２）: 10 分

解き方（２）: \(\dfrac{60 × 15}{90}\) = 10 [分]

【別解】
距離が一定のとき、速さと時間は反比例する。
分速 90 m の速さで走るとかかる時間を □ 分とすると、
\(\dfrac{1}{60}\)：\(\dfrac{1}{90}\) = 15：□
3：2 = 15：□
□ = 10 [分]

（３）分速 90 m で 10 分かかる道を、時速 4.5 km で進むと何分かかりますか。

答え（３）: 12 分

解き方（３）: 時速 4.5 km を分速 □ mにすると、
4.5 × 1000 ÷ 60 = 75 [m/分]
求める時間は、
\(\dfrac{90 × 10}{75}\) = 12 [分]

【別解】
距離が一定のとき、速さと時間は反比例する。
時速 4.5 kmの速さで進むとかかる時間を □ 分とすると、
\(\dfrac{1}{90}\)：\(\dfrac{60}{4.5 × 1000}\) = 10：□
5：6 = 10：□
□ = 12 [分]

（４）家と駅の間を車で移動するのに、行きは時速 63 km、帰りは時速 42 kmで走りました。往復の平均の速さは時速何 km ですか。

答え（４）: 時速 50.4 km

解き方（４）: 距離が一定のとき、速さと時間は反比例（逆比）となるので、
行きと帰りの時間の比は 42：63 で簡単な比にすると ②：③ で全体は ⑤ となる。
平均の速さ = 全体の距離 ÷ 全体の時間なので、
( 63 × ② + 42 × ③ ) ÷ ⑤ = 50.4 [km/時]

【別解】
距離が一定のとき、速さと時間は反比例する。
行きと帰りにかかった時間を比で表すと、
行き：帰り = \(\dfrac{1}{63}\)：\(\dfrac{1}{42}\) = 2：3 となる。よって、往復の平均の速さを時速 □ kmとすると、
\(\dfrac{1}{2\ ×\ 2}\)：\(\dfrac{1}{5}\) = 63：□
5：4 = 63：□
□ = \(\dfrac{4\ ×\ 63}{5}\) = 50.4 [km/時]

（５）5 時間で 320 km 走る車は、3 時間で何 km 走りますか。

答え（５）: 192km

解き方（５）: \(\dfrac{320}{5}\) × 3 = 192 [km]

【別解】
速さが一定のとき、時間と距離は比例する。
3 時間で □ km走るとすると、
5：320 = 3：□
□ = \(\dfrac{320 × 3}{5}\) = 192 [km]

（６）ある池の周りを A さんは 1 時間に 3 周、B 子さんは 1 時間に 4 周します。二人の速さの差は時速 3 kmです。二人の速さはそれぞれ時速何 kmですか。

答え（６）: A さん：時速 9 km　Bさん：時速 12 km

解き方（６）: 時間が一定のとき、距離と速さは比例する。
A さんと B さんの速さの比は、A：B = 3：4
A さんの速さを ③ とすると、B さんの速さは ④ と表すことができる。
④ – ③ = ① = 3より、
A さんの速さは、③ = 3 × 3 = 9 [km/時]
B さんの速さは、④ = 4 × 3 = 12 [km/時]

問３

1 周 500 m のコースを、1 周走るごとに何分か休みながら 6 周したところ、40 分で走り終わりました。走る速さは分速 120 m です。1 周走るごとに休んだ時間は何分ですか。

答え: 3 分

解き方: 走っていた時間は 500 × 6 ÷ 120 = 25 [分] より、休んだ時間は全体で 40 – 25 = 15 [分] である。
休んだ回数は 5 回なので、1 周走るごとに休んだ時間は 15 ÷ 5 = 3 [分]

問４

弟は家から学校までの道のりを分速 60 m で歩きました。兄は弟より 5 分遅く出発して、分速 80 mで走ったところ、弟と同じ時刻に学校に着きました。家から学校までの道のりは何 m ですか。

答え: 1200 m

解き方: 弟と兄が学校に着くまでにかかった時間の差は 5 分より、家から学校までの道のりを □ m とすると、
\(\dfrac{□}{60}\) – \(\dfrac{□}{80}\) = 5
□ × ( \(\dfrac{4}{240}\) – \(\dfrac{3}{240}\) ) = 5
□ × \(\dfrac{1}{240}\) = 5
□ = 1200 [m]

問５

家から 1.5 kmはなれた公園へ向かいます。弟は分速 150 mの速さで走って、兄は自転車で分速 250 mで移動します。2 人は同時に家を出て、兄は途中にあるコンビニに 5 分間立ち寄りました。どちらが何分早く公園に着きましたか。

答え: 弟が 1 分早く着いた

解き方: 弟が公園に着くまでにかかった時間は、1.5 × 1000 ÷ 150 = 10 [分]
兄が公園に着くまでにかかった時間は、1.5 × 1000 ÷ 250 + 5 = 11 [分]
よって、弟が 11 – 10 = 1 [分] 早く公園に着く。

問６

150 kmの道を、はじめは分速 750 m で進み、途中から時速 75 km で進んだところ、2 時間 10 分かかりました。分速 750 m で進んだのは何分間ですか。

答え: 25 分間

解き方: 時速 75 km = 75 × 1000 ÷ 60 = 1250 [m/分]、2 時間 10 分 = 130 分
つるかめ算で考えると、
( 1250 × 130 – 150 × 1000 ) ÷ ( 1250 – 750 )
= 250 × (5 × 130 – 150 × 4) ÷ { 250 × ( 5 – 3 ) }
= ( 650 – 600 ) ÷ ( 5 – 3 ) = 25 [分間]

問７

42 km の道のりを 60 分ごとに 10 分間休みながら、分速 70 m で歩きます。この道のりを歩き終えるのに何時間何分かかりますか。

答え: 11 時間 30 分

解き方: 60 分間で進む道のりは 60 × 70 = 4200 [m] = 4.2 [km] より、休憩の回数は 42 ÷ 4.2 – 1 = 9 [回]。よって、歩き終えるのにかかる時間は、
42 × 1000 ÷ 70 + 10 × 9 = 690 [分] = 11 時間 30 分

問８

姉は家から 1.5 kmはなれた学校へ分速 60 mで歩いて向かいます。姉が出発してから 2 分後に妹が家から学校へ向かったところ、妹は姉より 7 分遅く着きました。妹は分速何 m で歩きましたか。

答え: 分速 50 m

解き方: 姉が家から学校に着くまでにかかった時間は、1.5 × 1000 ÷ 60 = 25 [分]
妹が家から学校に着くまでにかかった時間は、25 + ( 7 – 2 ) = 30 [分] より、
1500 ÷ 30 = 50 [m/分]

問９

（１）A さんが家から図書館まで行くとき、家から図書館の手前の駐輪場までは自転車で行き、駐輪場から図書館までは坂道を分速 40 m で歩いて上ります。図書館から家に戻るときは、坂道を分速 80 mで歩いて駐輪場まで下り、駐輪場から家までは自転車で帰ります。下のグラフは、A さんが図書館に行くまでの様子を表したものです。グラフの横軸は A さんが家を出てからの時間、縦軸は家からの距離を表しています。

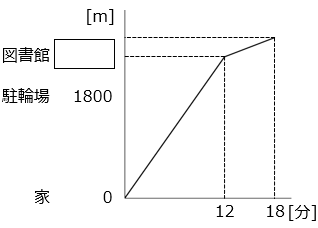
① A さんが自転車で進む速さは分速何 m ですか。

答え（１）- ①: 分速 150 m

解き方（１）- ①: グラフより、駐輪場までの距離は 1800 m、かかった時間は 12 分なので、
1800 ÷ 12 = 150 [m/分]

② グラフの \(\boxed{　　}\) に当てはまる数を答えなさい。

答え（１）- ②: 2040

解き方（１）- ②: グラフより、駐輪場から図書館に行くのにかかった時間は 18 – 12 = 6 [分] なので、駐輪場から図書館までは 40 × 6 = 240 [m]。よって、
\(\boxed{　　}\) に当てはまる数は、1800 + 240 = 2040

③ A さんは午前 10 時に家を出発して図書館に行き、着いてから 10 分後に図書館を出て家に帰りました。家に着いたのは何時何分ですか。

答え（１）- ③: 10 時 43 分

解き方（１）- ③: 図書館から駐輪場に着くまでにかかった時間は、240 ÷ 80 = 3 [分]。よって、家を出てから、家に帰るまでにかかった時間は、
18 + 10 + 3 + 12 = 43 [分]
家に着いたのは、10 時 43 分

④ ある日、A さんは図書館に行った帰りに、コンビニに立ち寄りました。コンビニは図書館から家に自転車で帰る道の途中にあります。A さんは午後 2 時 30 分に家を出て、図書館で 15 分過ごし、午後 3 時 15 分にコンビニに着きました。コンビニは家から何 mのところにありますか。

答え（１）- ④: 450 m

解き方（１）- ④: A さんが家を出てから図書館に入り図書館を出て駐輪場に着くまでにかかった時間は 18 + 15 + 3 = 36 [分間] より、その時間は午後 2 時 30 分の 36 分後の午後 3 時 6 分。
よって駐輪場からコンビニまでにかかった時間は 9 分なので、コンビニと家の距離は、
1800 – 9 × 150 = 450 [m]

（２）A さんと B さんは公園で会うことにしました。公園は A さんの家と B さんの家の間にあります。2 人は同じ時間に家を出て公園に向かって走り、同じ時間に公園に着きました。公園で 20 分間過ごした後、歩いて家に帰りました。2 人が家に着いた時間は同じでした。A さんの進む速さは、行きは分速 120 m、帰りは分速 40 mです。また、A さんの往復の道のりと B さんの往復の道のりの比は、2 : 3 でした。グラフはそのときの 2 人の様子を表したものです。

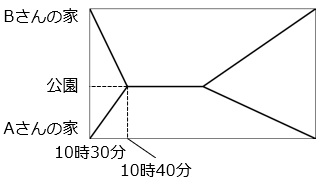
① 2 人が家に着いたのは何時何分ですか。

答え（２）- ①: 11 時 30 分

解き方（２）- ①: A さんについて考える。
A さんが行きにかかった時間は 10 分。距離が一定のとき、時間は速さに反比例するので、行きと帰りにかかった時間の比は、
\(\dfrac{1}{120}\)：\(\dfrac{1}{40}\) = 1：3
帰りにかかった時間は、行きの 3 倍なので、10 × 3 = 30 [分]
A さんと B さんが公園を出た時間は 11 時より、2 人が家に着いたのは 11 時 30 分。

② A さんの家から B さんの家までの道のりは何 km ですか。

答え（２）- ②: 3 km

解き方（２）- ②: A さんの家から公園までの道のりは、120 × 10 = 1200 [m] = 1.2 [km]
A さんの往復の道のりと B さんの往復の道のりの比（片道の道のりの比も同じ）は、2：3 より、A さんの家から B さんの家までの道のりを □ kmとすると、
2：5 = 1.2：□
□ = 3 [km]

③ B さんが家に帰るときの歩く速さは分速何 m ですか。

答え（２）- ③: 分速 60 m

解き方（２）- ③: 公園から B さんの家までの道のりは 3000 – 1200 = 1800 [m]、帰るのにかかった時間は 30 分より、
1800 ÷ 30 = 60 [m/分]

（３）A さんは家から 3400 m 離れた映画館まで歩いて行きました。A さんは途中公園で 20 分休み、家を出てから 85 分後に映画館に着きました。公園で休んだ後の歩く速さは、休む前の速さの \(\dfrac{2}{3}\) です。グラフは、A さんが映画館に着くまでに、家から歩いた道のりを表したものです。

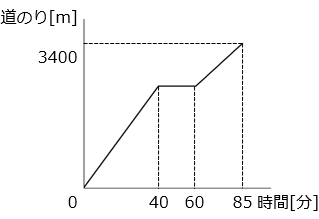
① 公園に着くまでの A さんの歩く速さは分速何 m ですか。

答え（３）- ①: 分速 60 m

解き方（３）- ①: 公園に着くまでの A さんの歩く速さを ③ とすると、公園で休んだ後の速さは ③ × \(\dfrac{2}{3}\) = ② と表すことができる。
家から公園までは 40 分、公園から映画館までは 25 分歩いたので、
③ × 40 + ② × 25 = 3400
① = 20
公園に着くまでのAさんの歩く速さは、③ = 3 × 20 = 60 [m/分]

② 公園は家から何 m のところにありますか。

答え（３）- ②: 2400 m

解き方（３）- ②: 60 × 40 = 2400 [m]

（４）グラフは走者 5 人が 3 kmずつ走ったときの時間と道のりを表しています。

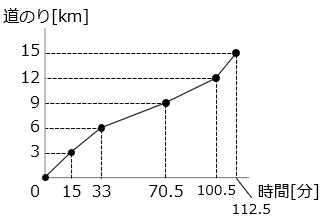
① 第 3 走者の速さは時速何 km ですか。

答え（４）- ①: 時速 4.8 km

解き方（４）- ①: グラフより、第 3 走者が 3 km走るのにかかった時間は 70.5 – 33 = 37.5 [分] = \(\dfrac{5}{8}\) [時間]。
3 ÷ \(\dfrac{5}{8}\) = 4.8 [km/時]

② 最も速い走者と最も遅い走者の速さの差は時速何 km ですか。

答え（４）- ②: 時速 10.2 km

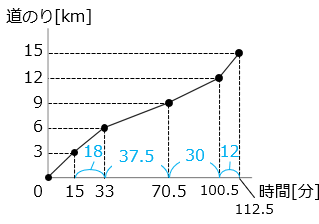
解き方（４）- ②: 最も遅い走者は第 3 走者で、その速さは ① より4.8 [km/時]
最も速い走者は第 5 走者で 3 km走るのにかかった時間は12 [分] = \(\dfrac{1}{5}\) [時間]
3 ÷ \(\dfrac{1}{5}\) = 15 [km/時]。よってその差は、
15 – 4.8 = 10.2 [km/時]

③ 5 人がそれぞれの速さで 30 分ずつ走ると、合わせて何 km になりますか。

答え（４）- ③: 23.9 km

解き方（４）- ③: それぞれの走者が3kmを走るのにかかった時間 [分] はグラフに記したとおりである。
3 ÷ 15 × 30 + 3 ÷ 18 × 30 + 3 ÷ 37.5 × 30 + 3 ÷ 30 × 30 + 3 ÷ 12 × 30
= 3 × 30 × (\(\dfrac{1}{15}\) + \(\dfrac{1}{18}\) + \(\dfrac{1}{37.5}\) + \(\dfrac{1}{30}\) + \(\dfrac{1}{12}\)) = 23.9 [km]

（５）A 君は家から 5 kmはなれた野球場へ行くために、家を出発して一定の速さで走っていました。疲れたので公園で 10 分間休み、その後は一定の速さで歩きました。グラフは A 君が野球場に着くまでの時間と道のりを表しています。

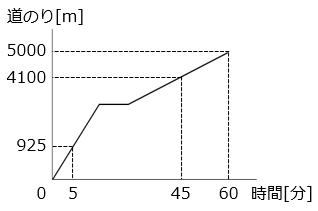
① A 君の走った速さは分速何 m ですか。

答え（５）- ①: 分速 185 m

解き方（５）- ①: グラフより 925 m 進むのに 5 分かかったので、
925 ÷ 5 = 185 [m/分]

② A君の歩いた速さは分速何 m ですか。

答え（５）- ②: 分速 60 m

解き方（５）- ②: グラフより 5000 – 4100 = 900 [m] 進むのに 60 – 45 = 15 [分] かかったので、
900 ÷ 15 = 60 [m/分]

③ A 君の家から公園までは何 m ですか。

答え（５）- ③: 2960 m

解き方（５）- ③: 走った道のりが公園までの道のりである。
つるかめ算の方法で走った時間を求める。
すべての道のりを歩いたとすると、その道のりは 60 × (60 – 10) = 3000 [m] となる。しかし、実際は 5000 m なので、走った時間は、
( 5000 – 3000 ) ÷ ( 185 – 60 ) = 16 [分]
よって、公園までの道のりは、
185 × 16 = 2960 [m]