算数【応用】比
問1
赤、白 2 種類の玉があり、赤玉 5 個と白玉 11 個の重さの比は 6:11 で、全部で 425 g です。赤玉 1 個の重さは何 g ですか。
- 答え
- 30 g
- 解き方
- 赤玉の重さは、425 × \(\dfrac{6}{17}\) = 150 [g] となる。
よって、150 ÷ 5 = 30 [g]
【別解】
赤玉 1 個の重さを □ g とすると、白玉 11 個の重さは 465 – 5 × □ [g] と表すことができる。
よって、 5 × □:425 – 5 × □ = 6:11
内項の積と外項の積は等しいので、
6 × ( 425 – 5 × □ ) = 11 × 5 × □
6 × 425 – 30 × □ = 55 × □
□ = 30 [g]
問2
100 円玉と 10 円玉の枚数の比が 3:4 で、合計金額が 4080 円でした。このとき、100 円玉は何枚ですか。
- 答え
- 36 枚
- 解き方
- 100 円の枚数を ③ すると、10 円玉の枚数は ④ と表すことができる。
100 × ③ + 10 × ④ = 4080
① = 12
100 円玉の枚数は、12 × 3 = 36 [枚]
問3
あめ 114 個とチョコレート 80 個を A、B、C の 3 人でそれぞれ分けました。あめは A:B = 5:3、B:C = 2:1、チョコレートは A:C = 3:1、B:C = 4:3になりました。このとき、B のあめとチョコレートの個数の比を、最も簡単な整数の比で答えなさい。
- 答え
- あめ:チョコレート = 9:5
- 解き方
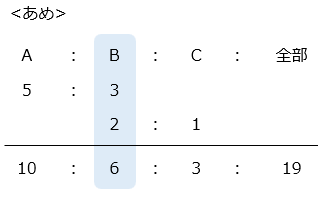
B のあめの個数は 114 × \(\dfrac{6}{19}\) = 36 [個]
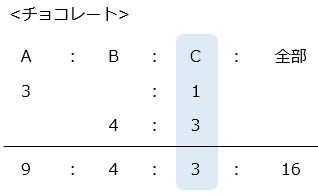
B のチョコレートの個数は 80 × \(\dfrac{4}{16}\) = 20 [個]
よって、B のあめとチョコレートの個数の比は、
あめ:チョコレート = 36:20 = 9:5
問4
A 君が 5 歩で進む距離を B 君は 7 歩で進み、A 君が 2 歩進む時間で B 君は 3 歩進みます。このとき、A 君と B 君の進む速さの比を求めなさい。
- 答え
- A 君:B 君 = 14:15
- 解き方
- 1 歩で進む距離は同じ距離を進む歩数に反比例する。
A 君と B 君が 1 歩で進む距離の比は、\(\dfrac{1}{5}\):\(\dfrac{1}{7}\) = 7:5 となる。
速さの比は同じ時間に進む距離の比に等しい。
A 君が 1 歩で進む距離を ⑦ とすると、A 君と B 君が同じ時間に進む距離の比は、
⑦ × 2:⑤ × 3 = ⑭:⑮
問5
A、B の 2 種類のおもりがあります。重さは A が 15 g、B が 25 g です。A と B の個数の比が 2:3 で、その重さが 630 g のとき、A と B のおもりはそれぞれ何個ありますか。
- 答え
- A:12 個 B:18 個
- 解き方
- A と B の重さの比は、A:B = 2 × 15:3 × 25 = 2:5 となる。
よって、
A だけの重さは 630 × \(\dfrac{2}{7}\) = 180 [g]、個数は 180 ÷ 15 = 12 [個]
B だけの重さは 630 × \(\dfrac{5}{7}\) = 450 [g]、個数は 450 ÷ 25 = 18 [個]
問6
A さんと B さんが持っているキャンディーの個数の比は 8:5 で、合計 78 個です。2 人とも同じ数ずつ食べたところ、残ったキャンディーの個数の比は 2:1 になりました。それぞれが食べたキャンディーの個数は何個ですか。
- 答え
- 12 個
- 解き方
- A さんと B さんが食べる前に持っていたキャンディーの個数は、
A さん:78 × \(\dfrac{8}{13}\) = 48 [個]
B さん:78 – 48 = 30 [個]
食べたキャンディーを □ 個とすると、
48 – □:30 – □ = 2:1
内項の積と外項の積は等しいので、
2 × ( 30 – □ ) = 48 – □
□ = 12 [個]
問7
A 君、B 君、C 君の 3 人が持っているおはじきの個数は全部で 98 個で、A 君と B 君の持っているおはじきの個数の比は 2:5、C 君は A 君の持っている個数の 3 倍より 7 個多く持っています。3 人の持っているおはじきの個数の比を求めなさい。
- 答え
- A:B:C = 2:5:7
- 解き方
- A 君が持っているおはじきの個数を ② とすると、B 君は ⑤、C 君は ② × 3 + 7 と表すことができる。よって、
② + ⑤ + ② × 3 + 7 = 98
① = 7
3 人の持っているおはじきの個数の比は、
A:B:C = 14:35:49 = 2:5:7
問8
52 個の碁石を長方形の形に並べたところ、縦と横の碁石の数の比が 5:9 になりました。このとき、縦の碁石の数は何個ですか。
- 答え
- 10 個
- 解き方
- 縦の碁石の数を ⑤ とすると、横の碁石の数は ⑨ と表すことができる。
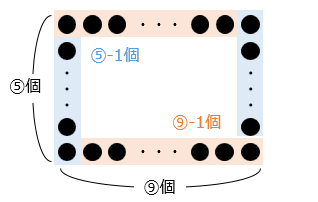
2 × ( ⑤ – 1 + ⑨ – 1 ) = 52
① = 2
よって、縦の碁石の数は、2 × 5 = 10 [個]
問9
A さん、B さん、C さんの 3 人のゲームの得点の平均点は 70 点でした。A さんと C さんの得点の比は 2:3 で、B さんの得点は C さんより 10 点高かったです。B さんの得点は何点ですか。
- 答え
- 85 点
- 解き方
- A さんの得点を ② とすると、C さんの得点は ③、B さんの得点は ③ + 10 と表すことができる。よって、
② + ③ + 10 + ③ = 70 × 3
① = 25
B さんの得点は、3 × 25 + 10 = 85 [点]
問10
キャンディーとチョコレートとキャラメルがそれぞれ何個かずつあります。キャンディーとチョコレートの個数の比は 3:5、キャンディーとキャラメルの個数の比は 7:4 で、キャンディーとチョコレートの個数の差は 28 個です。このときキャラメルは何個ありますか。
- 答え
- 24 個
- 解き方
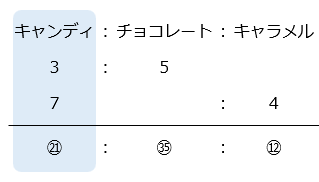
キャンディーとチョコレートの個数の差は 28 個なので、
㉟ – ㉑ = 28
① = 2
キャラメルの個数は、12 × 2 = 24 [個]




