- 面積の求め方
- 【三角形】
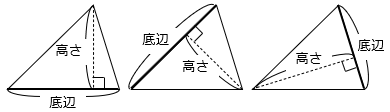
底辺 × 高さ ÷ 2
【四角形】
①正方形・長方形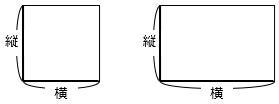
縦 × 横
②平行四辺形:2組の向かい合う辺が等しい四角形(正方形・長方形も含む)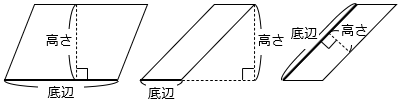
底辺 × 高さ
③台形:1組の向かい合う辺が平行な四角形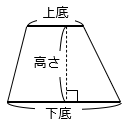
( 上底 + 下底 ) × 高さ ÷ 2
③ひし形:4つの辺の長さが等しい四角形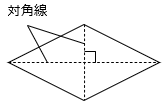
対角線 × 対角線 ÷ 2
※複雑な図形は、対角線を引くことで、知っている図形の組み合わせに変換しよう!
- 面積比
- 【高さの等しい三角形】
高さの等しい三角形の面積は底辺の比と等しい。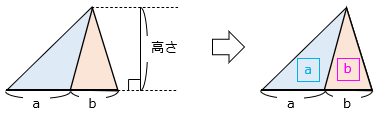
【底辺の等しい三角形】
底辺の等しい三角形の面積は高さの比と等しい。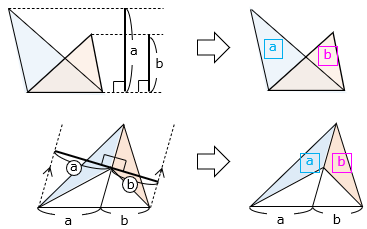
問1
図形の面積を求めなさい。
(1)
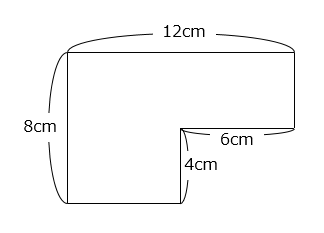
- 答え(1)
- 72cm2
- 解き方(1)
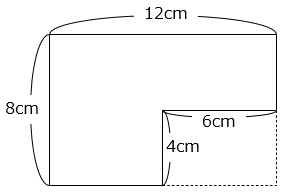
8 × 12 – 4 × 6 = 96 – 24 = 72(cm2)
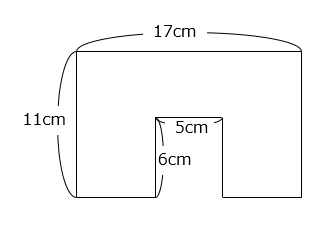
(2)
- 答え(2)
- 157cm2
- 解き方(2)
11 × 17 – 6 × 5 = 187 – 30 = 157(cm2)
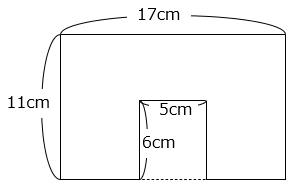
(3)
- 答え(3)
- 168cm2
- 解き方(3)
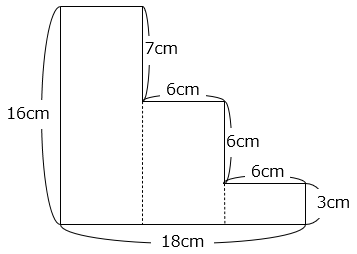
6 × 16 + 6 × 9 + 6 × 3
= 6 × (16 + 9 + 3)
= 6 × 28 = 168(cm2)
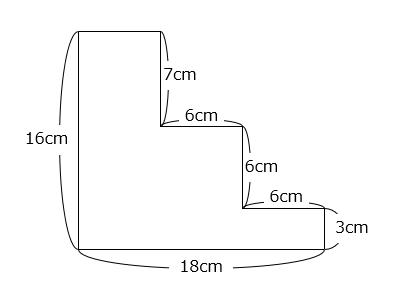
(4)
- 答え(4)
- 141cm2
- 解き方(4)
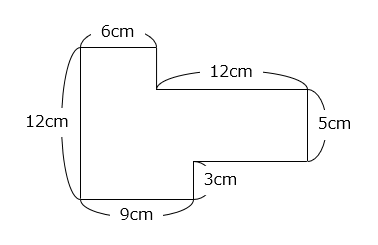
- 1) 分割して計算する方法

6 × 4 + 5 × 18 + 3 × 9 = 24 + 90 + 27 = 141(cm2)
2) 大きな長方形の面積から不要な部分を除く方法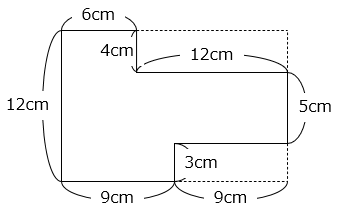
12 × 18 – 4 × 12 – 3 × 9 = 216 – 48 – 27 = 141(cm2)
※1)の方が計算が簡単
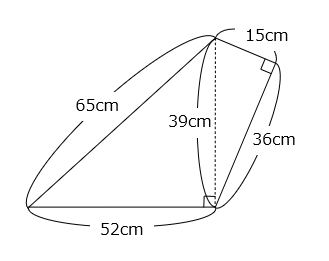
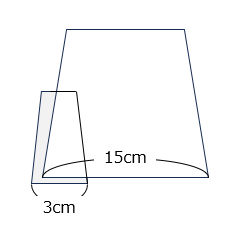
(5)2組の直角三角形をつなぎ合わせて四角形を作りました。この四角形の面積を求めなさい。
- 答え(5)
- 1284cm2
- 解き方(5)
- 52 × 39 ÷ 2 + 15 × 36 ÷ 2
= 1014 + 270 = 1284(cm2)
問2
の部分の面積を求めなさい。
(1)長方形と正方形を並べた図です。
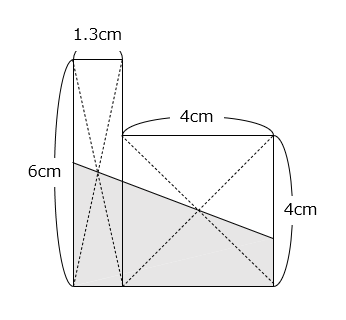
- 答え(1)
- 11.9cm2
- 解き方(1)
- ( 6 × 1.3 + 4 × 4 ) ÷ 2
= 23.8 ÷ 2 = 11.9(cm2)
※平行四辺形(正方形・長方形・ひし形を含む)を、対角線の交点を通る直線で2つに分割したとき、2つの四角形の面積は等しい!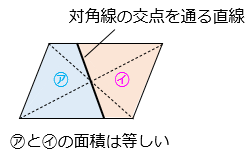
(2)
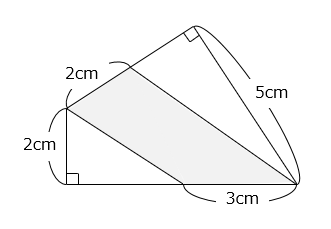
- 答え(2)
- 8cm2
- 解き方(2)
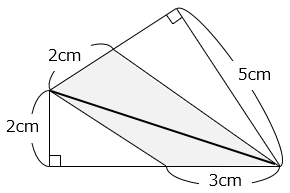
3 × 2 ÷ 2 + 2 × 5 ÷ 2 = 8(cm2)
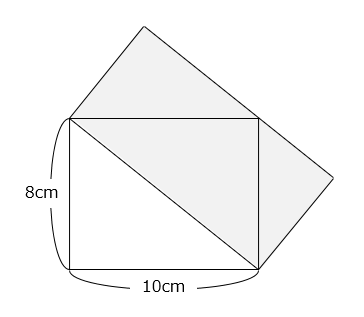
(3)2つの長方形が重なっています。
- 答え(3)
- 80cm2
- 解き方(3)
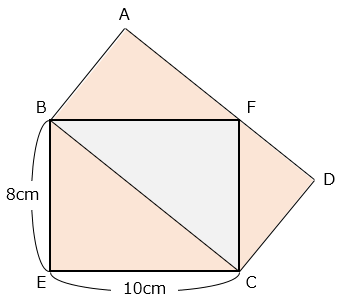
△ABFと△CDFの面積の和は△BCFの面積に等しく、△BCEとも等しい。よって、2つの長方形の面積は等しいので、
8 × 10 = 80(cm2)
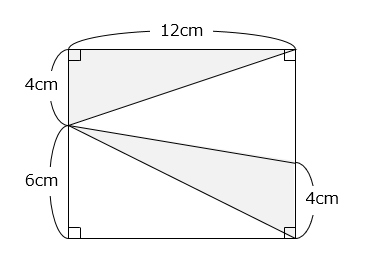
(4)
- 答え(4)
- 48cm2
- 解き方(4)
- 4 × 12 ÷ 2 × 2 = 48(cm2)
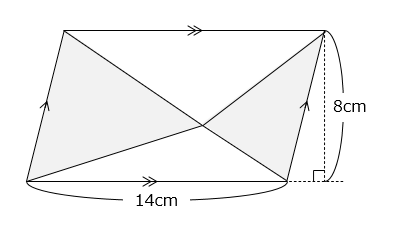
(5)
- 答え(5)
- 56cm2
- 解き方(5)

求める面積は、平行四辺形を2等分した三角形の面積に等しい。
14 × 8 ÷ 2 = 56(cm2)
問3
1辺10cmの正方形の紙を縦横4cmずつずらして3枚重ねました。
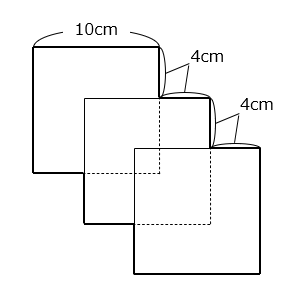
(1)太線で囲まれた部分の面積を求めなさい。
- 答え(1)
- 228cm2
- 解き方(1)
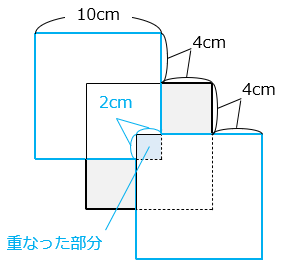
青線で囲った部分とグレーの部分の面積の和と考えると、
(10 × 10 × 2 – 2 × 2) + 4 × 4 × 2 = 228(cm2)
(2)2重になった部分の面積を求めなさい。
- 答え(2)
- 64cm2
- 解き方(2)
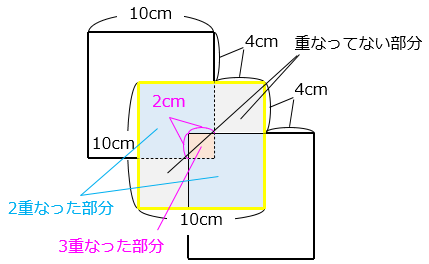
真ん中の正方形から、重なっていない部分と3重になった部分を除く。
10 × 10 – 4 × 4 × 2 – 2 × 2 = 64(cm2)
問4
図形の面積は130cm2でした。□の値を求めなさい。
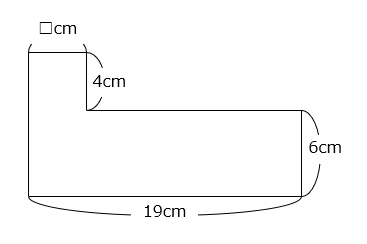
- 答え
- 4
- 解き方
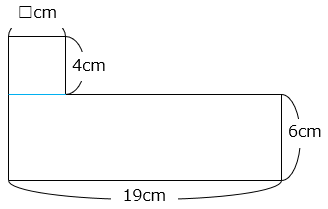
4 × □ + 6 × 19 = 130
4 × □ = 130 – 114 = 16
□ = 4(cm)
問5
㋐と㋑の面積が等しいとき、□の値を求めなさい。
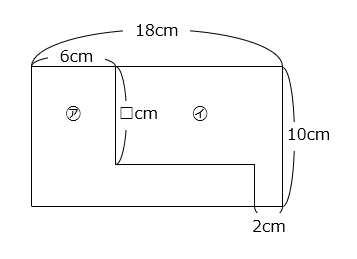
- 答え
- 7
- 解き方
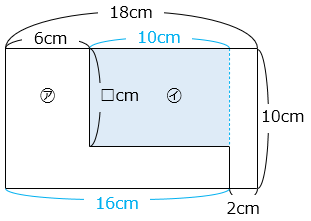
㋐ = ㋑
10 × 16 – 10 × □ = 2 × 10 + 10 × □
20 × □ = 140
□ = 7(cm)
問6
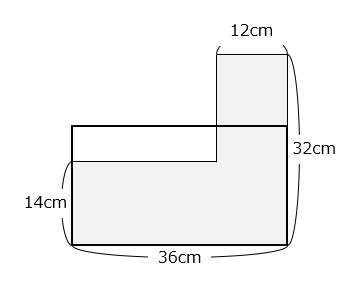
太線で囲まれた長方形の面積と、 の面積が等しいとき、太線で囲まれた長方形の縦の長さは何cmですか。
- 答え
- 20cm
- 解き方
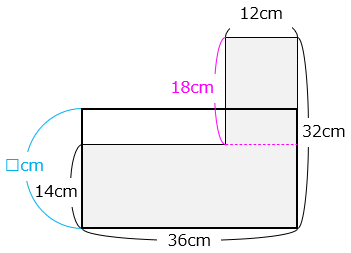
太線で囲まれた長方形の縦の長さを□cmとする。
36 × □ = 36 × 14 + 12 × 18
2 × □ = 2 × 14 + 12 × 1 = 40
□ = 20(cm)
問7
正方形の1辺を2cm伸ばしたところ、その正方形の面積はもとの正方形よりも44cm2大きくなりました。もとの正方形の面積を求めなさい。
- 答え
- 100cm2
- 解き方
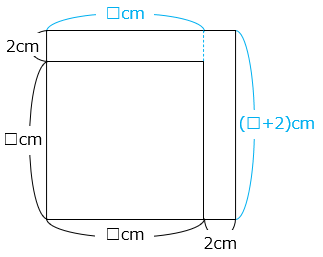
もとの正方形の1辺の長さを□cmとする。
□ × 2 + 2 ×( □ + 2 ) = 44
4 × □ = 40
□ = 10(cm)
よってもとの正方形の面積は 10 × 10 = 100(cm2)
問8
(1)面積15.12cm2の長方形があります。たての長さが4.2cmのとき、横の長さは何cmですか。
- 答え(1)
- 3.6cm
- 解き方(1)
- 15.12 ÷ 4.2 = 3.6(cm)
(2)たて3cm、横12cmの長方形の面積と同じ面積の正方形の1辺の長さは何cmですか。
- 答え(2)
- 6cm
- 解き方(2)
- 長方形の面積は 3 × 12 = 36(cm2)
36 = 6 × 6 より、正方形の1辺の長さは6cm
問9
周りの長さが84cmの長方形があります。横の長さが縦の長さの1.1倍のとき、この長方形の面積を求めなさい。
- 答え
- 440cm2
- 解き方
- 縦の長さを□cmとすると、横の長さは ( 1.1 × □ ) cmと表すことができる。長方形の周りの長さは縦と横の長さの和を2倍なので、
□ + 1.1 × □ = 84 ÷ 2
2.1 × □ = 42
□ = 20(cm)
1.1 × □ = 1.1 × 20 = 22(cm)
よって長方形の面積は、
20 × 22 = 440(cm2)
問10
図の四角形は対角線BDの長さが18cmのひし形です。対角線ACより右側( の部分)の面積は45cm2です。
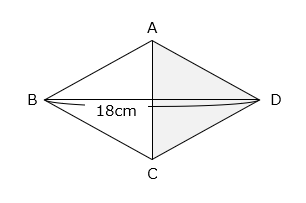
(1)このひし形の面積を求めなさい。
- 答え(1)
- 90cm2
- 解き方(1)
- ひし形の場合、対角線で2分割された面積は互いに等しいので、
45 × 2 = 90(cm2)
(2)対角線ACの長さを求めなさい。
- 答え(2)
- 10cm
- 解き方(2)
- ひし形の面積は 対角線 × 対角線 ÷ 2 で求められる。
18 × AC ÷ 2 = 90
AC = 10(cm)
【別解】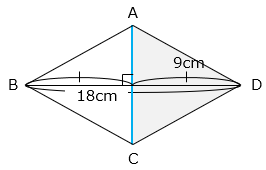
△ADC( )は、対角線ACを底辺とした高さ9cmの三角形である。よって、
AC × 9 ÷ 2 = 45
AC = 10(cm)
問11
1めもり1cmの方眼紙があります。 部分の面積を求めなさい。
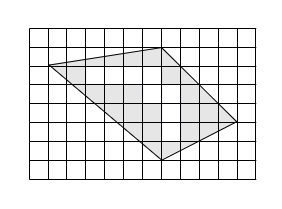
- 答え
- 22cm2
- 解き方
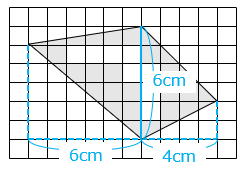
四角形の面積は2つの三角形が組み合わさってできていると考えると、
6 × 6 ÷ 2 + 6 × 4 ÷ 2 = 30(cm2)
方眼紙1マスの面積は 1 × 1 = 1(cm2)で、四角形の中に白いマスは8個あり、その面積は 8cm2
求める面積は、
30 – 8 = 22(cm2)
問12
(1)点Dは辺BCを 1:3 に分けた点で、点Eは辺ACを 1:5 に分けた点です。三角形AFEの面積が5cm2のとき、三角形ABCの面積を求めなさい。
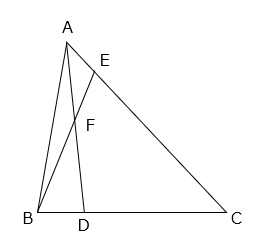
- 答え(1)
- 90cm2
- 解き方(1)
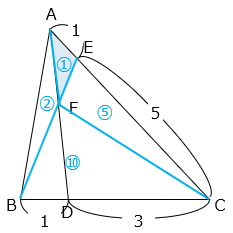
△AFEの面積を①とすると、
△AFEと△CFEは高さが等しく、底辺の比が 1:5 より△CFE = ⑤
△AFCと△AFBは底辺が等しく、高さの比が 3:1 より△AFB = ⑥ × \(\dfrac{1}{3}\) = ②
△AFBと△BFCは底辺が等しく、高さの比が 1:5 より△BFC = ② × 5 = ⑩ となる。
△ABCの面積は上記の各三角形の面積の和なので、
△ABC = ① + ⑤ + ② + ⑩ = ⑱
① = 5(cm2) より、⑱ = 18 × 5 = 90(cm2)
(2)三角形ABCの面積が180cm2のとき、四角形BCEDの面積を求めなさい。
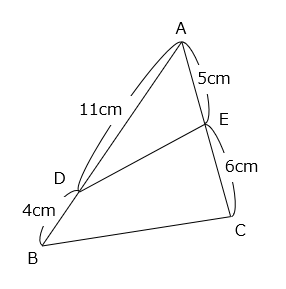
- 答え(2)
- 120cm2
- 解き方(2)
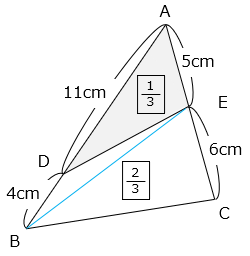
△ABCの面積を \(\boxed{1}\) とすると、
△ADE = \(\boxed{1}\) × \(\dfrac{5}{11}\) × \(\dfrac{11}{15}\) = \(\boxed{\dfrac{1}{3}}\)
□BCED = \(\boxed{1}\) – \(\boxed{\dfrac{1}{3}}\) = \(\boxed{\dfrac{2}{3}}\)
\(\boxed{1}\) = 180(cm2)より、\(\boxed{\dfrac{2}{3}}\) = \(\dfrac{2}{3}\) × 180 = 120(cm2)
【別解】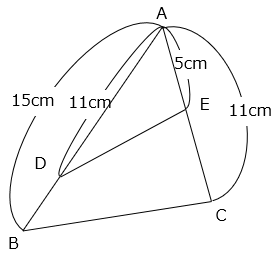
△ABC:△ADE = 15 × 11:11 × 5 = 3:1
180:△ADE = 3:1
3 × △ADE = 180
△ADE = 60(cm2)
□BCED = 180 – 60 = 120(cm2)
(3)図のような1辺10cmの正方形ABCDがあります。CEを 3:2 に分ける点をFとします。 部分の面積を求めなさい。
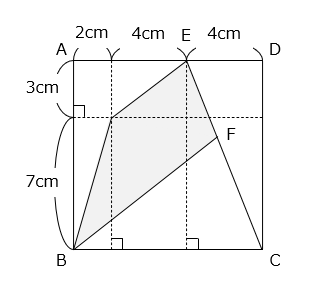
- 答え(3)
- 31cm2
- 解き方(3)
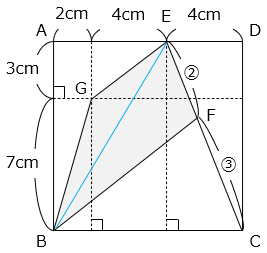
部分の面積(□BFEG)は、△BEGと△BEFの和である。
△BEG:△AEBから白色の部分を引く
= 6 × 10 ÷ 2 – ( 2 × 3 + 2 × 7 ÷ 2 + 4 × 3 ÷ 2 )
= 30 – ( 6 + 7 + 6 ) = 11(cm2)
△BEF
= △BEC × \(\dfrac{2}{5}\)
= 10 × 10 ÷ 2 × \(\dfrac{2}{5}\) = 20(cm2)
□BFEG = 11 + 20 = 31(cm2)
問13
(1)大小2つの四角形が重なっています。重なった部分の面積は、小さい四角形の \(\dfrac{3}{4}\) で、大きい四角形の \(\dfrac{4}{15}\) です。大きい四角形の面積が360cm2のとき、 部分の面積を求めなさい。
- 答え(1)
- 32cm2
- 解き方(1)
- 重なった部分の面積は 360 × \(\dfrac{4}{15}\) = 96(cm2)
これは小さい四角形の \(\dfrac{3}{4}\) にあたり、求める面積は小さい四角形の \(\dfrac{1}{4}\) である。よって、
96 ÷ 3 = 32(cm2)
(2)図のように三角形と四角形が重なっています。重なっている 部分の面積が、三角形の \(\dfrac{4}{13}\)、四角形の \(\dfrac{2}{5}\) であるとき、四角形の面積は三角形の面積の何倍ですか。
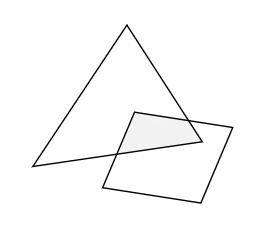
- 答え(2)
- \(\dfrac{10}{13}\) 倍
- 解き方(2)
- 部分の面積を \(\boxed{1}\) とすると、
三角形の面積は \(\boxed{\dfrac{13}{4}}\)、四角形の面積は \(\boxed{\dfrac{5}{2}}\) と表すことができる。よって、
\(\boxed{\dfrac{5}{2}}\) ÷ \(\boxed{\dfrac{13}{4}}\) = \(\dfrac{5}{2}\) × \(\dfrac{4}{13}\) = \(\dfrac{10}{13}\) (倍)
【ヒント:わり算の考え方】
わり算は、わった単位の1あたりの数が求められます。
例えば、10個のアメを5人で分ける場合は、10 ÷ 5 = 2
この答えの2の数は、わった単位の「1人あたり」という意味をもち、1人あたり2個のアメという意味になります。
よって、今回の問題では、三角形1あたり四角形は何倍ですかという問題なので、必ず \(\boxed{\dfrac{13}{4}}\) で割ってください。
