算数【基本】年齢算

問１

（１）現在、Aさんは8歳でお母さんは40才です。お母さんの年れいがAさんの年れいの3倍になるのは何年後ですか。

答え（１）

8年後

解き方（１）

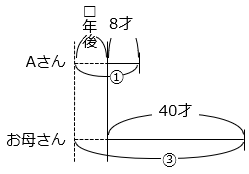
□年後お母さんの年れいがAさんの年れいの3倍になるのを線分図で表した。
図より、
③ – ① = 40 – 8
② = 32
① = 16
□ = 16 – 8 = 8(年後)

【別解①】比で考える
現在　Aさん：お母さん = 8：40 = 1：5
□年後　Aさん：お母さん = 1：3
現在も□年後も、Aさんとお母さんの年の差は変わらないので、差をそろえる。

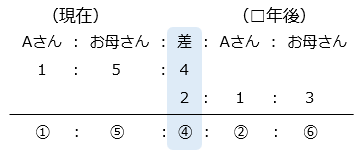
① = 8より、□年後のAさんの年れいは、② = 8 × 2 = 16(才)
よって、16 – 8 = 8(年後)

【別解②】式をつくる
お母さんの年れいがAさんの年れいの3倍になるのを□年後とすると、□年後、Aさんは 8 + □ (才)、お母さんは 40 + □ (才)と表すことができる。
2人の年れいの関係を式で表すと、
40 + □ = ( 8 + □ ) × 3
3 × □ – □ = 40 – 24
2 × □ = 16
□ = 8(年後)

（２）今から3年前、母の年れいは子どもの年れいの4倍でしたが、今から11年後、母の年れいは子どもの年れいの2倍になります。現在の子どもの年れいは何才ですか。

答え（２）

10才

解き方（２）

【線分図で解く①】

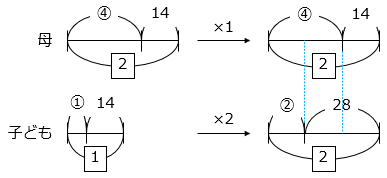
3年前の子どもの年れいを①、11年後の子どもの年れいを1⃣として、線分図を表した。
図より、
④ – ② = 28 – 14
② = 14
① = 7(才)
よって現在の子どもの年れいは 7 + 3 = 10(才)

【線分図で解く②】

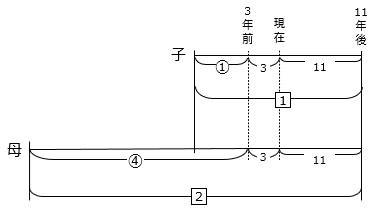
3年前の子どもの年れいを①、11年後の子どもの年れいを1⃣として、線分図を表した。
図より、
2⃣ – 1⃣ = ③
子の線分図より、③ – ① = 3 + 11
② = 14
① = 7(才)
よって現在の子どもの年れいは 7 + 3 = 10(才)

【別解①】比で考える
3年前　子ども：母 = 1：4
11年後　子ども：母 = 1：2
3年前も11年後も、子どもと母の年の差は変わらないので、差をそろえる。

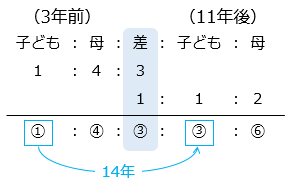
③ – ① = ② = 14
① = 7(才)
よって現在の子どもの年れいは 7 + 3 = 10(才)

【別解②】式をつくる
3年前の子どもの年れいを□才とすると、母の年れいは 4 × □ (才)と表すことができる。
11年後の2人の年れいの関係を式で表すと、
4 × □ + 14 = ( □ + 14 ) × 2
4 × □ – 2 × □ = 28 – 14
2 × □ = 14
□ = 7(才)
よって現在の子どもの年れいは 7 + 3 = 10(才)

（３）Aさんの父親は、Aさんより32才上です。5年後、Aさんの父親は、Aさんの年れいの5倍になります。今、Aさんの年れいは何才ですか。

答え（３）

3才

解き方（３）

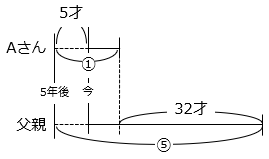
線分図より
⑤ – ① = 32
④ = 32
① = 8
8 – 5 = 3(才)

【別解】式をつくる
今のAさんの年れいを□才とすると、父親の年れいは □ + 32 (才)と表すことができる。
5年後の2人の年れいの関係を式で表すと、
□ + 32 + 5 = ( □ + 5 ) × 5
5 × □ – □ = 37 – 25
4 × □ = 12
□ = 3(才)

問２

（１）母親の年れいは32才、子どもの年れいは7才と4才です。2人の子どもの年れいの和が母親の年れいと等しくなるのは、何年後ですか。

答え（１）

21年後

解き方（１）

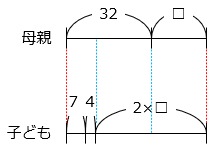
2人の子どもの年れいの和が母親の年れいと等しくなるのを□年後として、線分図を表した。
図より、
2 × □ – □ = 32 – (7 + 4 )
□ = 21(年後)

【別解】式をつくる
2人の子どもの年れいの和が母親の年れいと等しくなるのを□年後とすると、□年後の母親の年れいは 32 + □ (才)、子どもの年れいは 7 + □ (才) と 4 + □ (才) と表すことができる。
5年後の母親と2人の子どもの年れいの関係を式で表すと、
32 + □ = ( 7 + □ ) + ( 4 + □ )
2 × □ – □ = 32 – 11
□ = 21(年後)

（２）父は45才、兄は11才、妹は9才です。兄と妹の年れいの合計の3倍と父の年れいが等しかったのは、何年前ですか。

答え（２）

3年前

解き方（２）

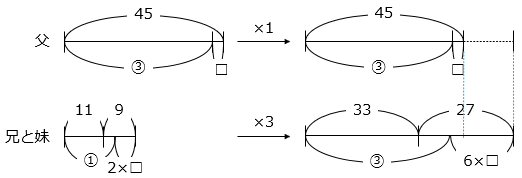
兄と妹の年れいの合計の3倍と父の年れいが等しかったのを□年前として、線分図を表した。
図より、
6 × □ – □ = ( 33 + 27 ) – 45
5 × □ = 15
□ = 3(年前)

【別解】式をつくる
兄と妹の年れいの合計の3倍と父の年れいが等しかったのを□年前とすると、□年前の父は 45 – □ (才)、兄は 11 – □ (才)、妹は 9 – □ (才) と表すことができる。
□年前の父と兄と妹の年れいの合計の関係を式で表すと、
45 – □ = {( 11 – □ ) + ( 9 – □ )} × 3
45 – □ = ( 20 – □ – □ ) × 3
45 – □ = 60 – 3 × □ – 3 × □
3 × □ + 3 × □ – □ = 60 – 45
5 × □ = 15
□ = 3(年前)

（３）現在、父は43才、母は37才、2人の子どもはそれぞれ12才と8才です。父と母の年令の和が、2人の子どもの年令の和の3倍になるのは、今から何年後ですか。

答え（３）

5年後

解き方（３）

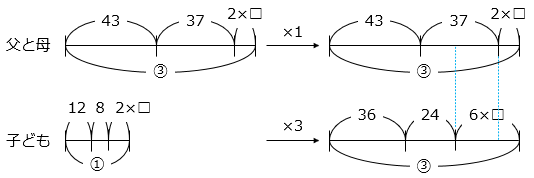
父と母の年令の和が、2人の子どもの年令の和の3倍になるのを□年後として、線分図を表した。
図より、
6 × □ – 2 × □ = ( 43 + 37 ) – ( 36 + 24 )
4 × □ = 80 – 60 = 20
□ = 5(年後)

【別解】式をつくる
父と母の年令の和が、2人の子どもの年令の和の3倍になるのを□年後とすると、□年後の父は 43 + □ (才)、母は 37 + □ (才)、2人の子どもは 12 + □ (才)、8 + □ (才) と表すことができる。
□年後の父と母の年令の和と2人の子どもの年令の和の関係を式で表すと、
( 43 + □ ) + ( 37 + □ ) = {( 12 + □ ) + ( 8 + □ )} × 3
80 + 2 × □ = ( 20 + 2 × □ ) × 3
80 + 2 × □ = 60 + 6 × □
6 × □ – 2 × □ = 80 – 60
4 × □ = 20
□ = 5(年後)