算数【入試】年齢算

問１

現在の母の年齢は子どもの年齢の5倍です。21年後には母の年齢は子どもの年齢の2倍になります。現在の子どもの年齢は何才ですか。

答え

7才

解き方

母と子どもの年齢の差は21年後も変わらないので、差に注目して連比を考える。

子どもは④ – ① = ③増加しており、これが21年にあたるので、現在の子どもの年齢は① = 7(才)

問２

父、母、花子の3人家族で、現在母の年齢は花子の年齢の4倍で、3人の年齢の合計は78才です。2年後には、父の年齢が花子の年齢の4倍になります。現在の花子の年齢を求めなさい。

答え

8才

解き方

現在の花子の年齢を①とすると、母の年齢は④、父の年齢は78 – ⑤となる。2年後、花子の年齢は① + 2、父の年齢は80 – ⑤となる。よって、
4 × (① + 2) = 80 – ⑤
① = 8(才)

問３

太郎君の今から9年後の年齢は、今から3年前の年齢の4倍になります。太郎君の今の年齢は何才ですか。

答え

7才

解き方

太郎君の3年前の年齢を①とすると、9年後の年齢は④となる。今の年齢に注目すると、
① + 3 = ④ – 9
① = 4
よって、今の年齢は、4 + 3 = 7(才)

問４

祖父、父、母、姉、弟の5人家族の年齢について次のことがわかっています。現在の祖父の年齢は何才ですか。

・現在、父と弟の年齢の合計は、母と姉の年齢の合計と同じ

・現在、弟の年齢は父の年齢の\(\dfrac{1}{5}\)

・12年前、祖父の年齢は父の年齢の2倍

・3年後、母と姉の年齢の合計は弟の年齢の5倍

答え

78才

解き方

現在の弟の年齢を①とすると、父の年齢は⑤となる。母と姉の年齢の合計は、(① + 3) × 5 -3 × 2 = ⑤ + 9で、これが父と弟の年齢の合計に等しい。
⑤ + 9 = ① + ⑤
① = 9
よって、父の年齢は5 × 9 = 45(才)とわかる。現在の祖父の年齢は、(45 – 12) × 2 + 12 = 78(才)

問５

父親、母親、長男、次男、三男の5人家族がいます。現在、この家族の年齢の和は125才ですが、10年前の家族の年齢の和は79才でした。また、3年後には長男が家を出ることを予定しているため、同居している家族の年齢の和は119才になります。ただし、子どもの年齢はすべて異なるものとします。

(1) 現在、三男は何才ですか。

(2) 現在、長男は何才ですか。

(3) 現在、母親の年齢は次男の年齢の4倍よりも4才年上で、父親よりも3才年下です。現在、父親は何才ですか。

答え(1)

6才

答え(2)

18才

答え(3)

47才

解き方(1)

現在と10年前の家族の年齢の和の差は、125 – 79 = 46 < 50であることから、10年前には三男は生まれていない。よって、三男は、46 – 4 × 10 = 6(才)

解き方(2)

現在の長男を除いた家族の年齢の和は、119 – 4 × 3 = 107(才)である。よって、長男の年齢は、125 – 107 = 18(才)

解き方(3)

現在の父親、母親、次男の年齢の和は、125 – 6 – 18 = 101(才)である。次男の年齢を①とおくと、父親、母親の年齢は図のようにあらわすことができる。

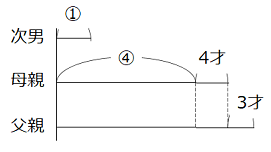
① + ④ × 2 = 101 – 4 × 2 – 3
① = 10
父親の年齢は、10 × 4 + 7 = 47(才)