理科【基本】重さと体積と浮力

問１

いろいろな体積の木、ねん土、水の重さを表とグラフにまとめました。体積と重さの関係について、\(\boxed{　}\) に当てはまる言葉を答えなさい。

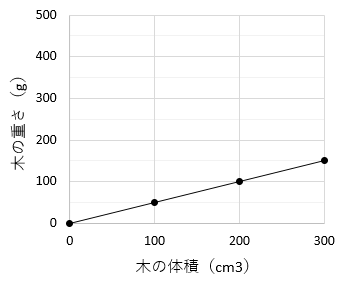
木の体積 (cm³)	0	100	200	300
木の重さ (g)	0	50	100	150

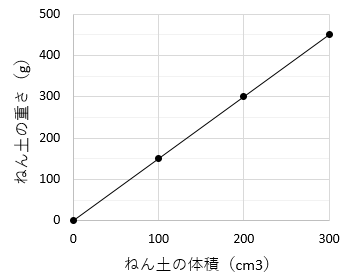
ねん土の体積 (cm³)	0	100	200	300
ねん土の重さ (g)	0	150	300	450

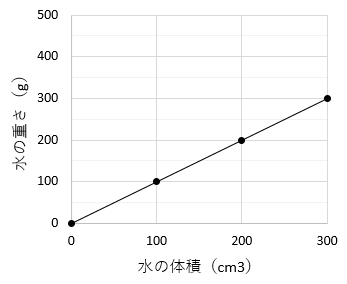
水の体積 (cm³)	0	100	200	300
水の重さ (g)	0	100	200	300

（１）物の体積と重さには \(\boxed{　}\) の関係があります。

（２）物の体積と重さの関係は、どのグラフも \(\boxed{①}\) を通り、線は \(\boxed{②}\) になります。

答え: （１）正比例（比例）
（２）①：原点　②：直線

問２

木の体積と重さを調べて表にまとめました。

木の体積 (cm³)	0	100	200	300
木の重さ (g)	0	80	160	240

（１）木の体積が500cm³のとき、木の重さは何gですか。

答え（１）: 400g

解説（１）: 500cm³は100cm³の5倍である。体積と重さは比例の関係にあるので、体積が5倍になると、重さも5倍になる。よって、80 × 5 = 400(g)

（２）木の重さが560gのとき、木の体積は何cm³ですか。

答え（２）: 700cm³

解説（２）: 560gは80gの7倍である。体積と重さは比例の関係にあるので、重さが7倍になると、体積も7倍になる。よって、100 × 7 = 700(cm³)

問３

図のように300cm³、150gの木と50cm³、60gのねん土を水に入れたとき、木は浮き、ねん土は沈みました。この現象について、\(\boxed{　}\) に当てはまる言葉を答えなさい。

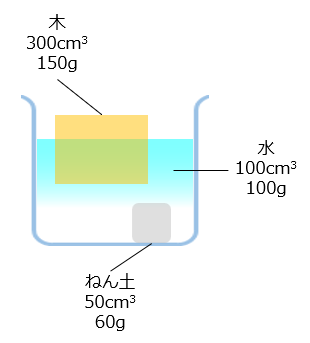
（１）同じ体積の木、ねん土、水の重さを比べたとき、最も重いものは \(\boxed{①}\) で、最も軽いものは \(\boxed{②}\) です。

答え（１）: ①：ねん土　②：木

解説（１）: それぞれの100cm³の重さは、木は50g、ねん土は120g、水は100gです。

（２）同じ体積で比べたとき、水よりも \(\boxed{①}\) 物は浮き、水より \(\boxed{②}\) 物は沈みます。

答え（２）: ①：軽い　②：重い

問４

表のようなA～Fの物質があります。

	A	B	C	D	E	F
体積 (cm³)	4	10	15	24	30	40
重さ (g)	8	5	45	8	60	20

（１）A～Fを水の中に入れました。水に浮くものはどれですか。

答え（１）: B、D、F

解説（１）: 水は1cm³、1gです。1cm³あたりの重さが1gより軽いものが浮きます。1cm³あたりの重さは「重さ ÷ 体積」で求めることができます。すなわち、重さの値より体積の値が大きいものが浮きます。
1cm³あたりの重さを求めると、
A : 8 ÷ 4 = 2(g)
B : 5 ÷ 10 = 0.5(g)
C : 45 ÷ 15 = 3(g)
D : 8 ÷ 24 = \(\dfrac{1}{3}\)(g)
E : 60 ÷ 30 = 2(g)
F : 20 ÷ 40 = 0.5(g)

（２）A～Fの中で、同じ種類の物質と考えられるのはどれとどれですか。

答え（２）: AとE、BとF

解説（２）: 「1cm³あたりの重さが等しい = 体積と重さが正比例の関係にある」ものが同じ種類の物質と考えられます。
A : 8 ÷ 4 = 2(g)
B : 5 ÷ 10 = 0.5(g)
C : 45 ÷ 15 = 3(g)
D : 8 ÷ 24 = \(\dfrac{1}{3}\)(g)
E : 60 ÷ 30 = 2(g)
F : 20 ÷ 40 = 0.5(g)

問５

メスシリンダーを使って、物体の体積を測りました。

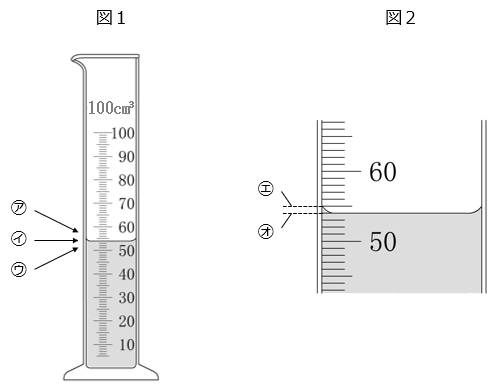
（１）メスシリンダーに水を入れると図１のようになりました。水の体積をはかるとき、㋐～㋒のどの位置から目盛りを読みますか。

答え（１）: ㋑

解説（１）: 液面と同じ高さから見ます

（２）図２は、図１の水面部分を拡大したものです。水の体積を読み取るとき、㋓、㋔のどちらの目盛りを読みますか。

答え（２）: ㋔

解説（２）: 液面の中央の平らなところの値を読みます。

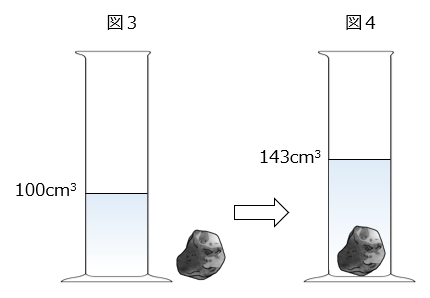
（３）図３の水の中に石を入れたところ、図４のようになりました。この石の体積は何cm³ですか。

答え（３）: 43cm³

解説（３）: 水の入ったメスシリンダーの中に物体を入れると、物体はその体積分の水を押しのけるため、メスシリンダーの液面があがります。よって、物体の体積は、物体を入れた後の体積と物体を入れる前の体積の差になります。
143 – 100 = 43(cm³)

問６

図１のように、体積20cm³の物体をばねはかりでつるすと、100gを示しました。

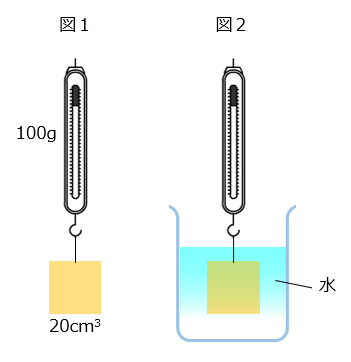
（１）\(\boxed{　}\) に当てはまる言葉、または数を答えなさい。

物体を水中に入れたときに働く力を \(\boxed{①}\) といいます。このとき、「\(\boxed{①}\) = 水1cm³の \(\boxed{②}\) × おしのけた水の \(\boxed{③}\)」が成り立ちます。

図２のとき、\(\boxed{①}\) は \(\boxed{④}\) gです。

答え（１）: ①：浮力　②：重さ　③：体積　④：20

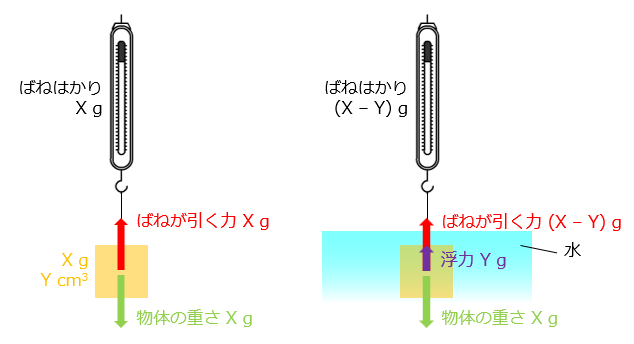
解説（１）: ※浮力は水以外の液体中や気体中でも働きます。
浮力 = 液体または気体の1cm³の重さ × おしのけた液体または気体の体積
※1cm³の重さは物質によって変わります。水の場合は、1gです。

（２）図２のとき、ばねはかりは何gを示しますか。

答え（２）: 80g

解説（２）: ばねはかりが示す重さは、
物体の重さ – 浮力 = 100 – 20 = 80(g)

問７

表に示した物体A、B、Cがあります。\(\boxed{　}\) に当てはまる言葉を答えなさい。

	A	B	C
体積 (cm³)	50	200	500
重さ (g)	100	200	300

（１）物体A、B、Cの同じ体積での重さは、\(\boxed{①}\) > \(\boxed{②}\) > \(\boxed{③}\) となります。

答え（１）: ①：A　②：B　③：C

解説（１）: 物体A、B、Cの100cm³の重さは、A 200g、B 100g、 C 60gです。

（２）物体A、B、Cを水の入った水そうに入れました。このとき、

　　Aは、\(\boxed{　①　}\) 。

　　Bは、\(\boxed{　②　}\) 。

　　Cは、\(\boxed{　③　}\) 。

（「水に浮きました」「水中で止まりました」「水にしずみました」から選択）

答え（２）: ①：水にしずみました　②：水中で止まりました　③：水に浮きました

解説（２）: 同じ体積で考えたとき、水より軽いものが浮き、同じものは水中で止まり、重いものはしずみます。
(水100cm³は100g)

問８

体積140cm³、重さ100gの物体を水そうに入れると、物体は浮きました。

（１）物体が受けている浮力は何gですか。

答え（１）: 100g

解説（１）: 物体が浮いているとき、物体の重さは浮力と等しくなっています。

（２）物体の一部は水面下にあります。水面下にある部分の体積は何cm³ですか。

答え（２）: 100cm³

解説（２）: 浮力は、「水1cm³の重さ(1g) × おしのけた水の体積(水面下にある部分の体積)」です。