算数【基本】流水算

流水算

船が流れに反して川を上るとき、船は川の流れの分だけ遅くなる。船が流れに乗って川を下るとき、船は川の流れの分だけ速くなる。

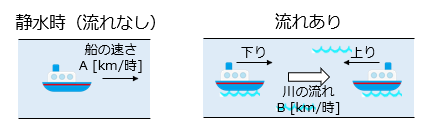
●上りの速さ：A – B [km/時]
●下りの速さ：A + B [km/時]

川の流れが一定のとき
●静水時の船の速さ：( 上りの速さ + 下りの速さ ) ÷ 2
●川の流れの速さ：( 下りの速さ – 上りの速さ ) ÷ 2
※川の流れの速さが上るときと下るときで変わる場合は使えない

問１

（１）時速5kmで流れている川があります。この川を船で3.6時間下ったところ、54km進みました。静水時の船の速さは時速何kmですか。

答え（１）

時速10km

解き方（１）

川を下る速さは、54 ÷ 3.6 = 15(km/時)
よって静水時の船の速さは、15 – 5 = 10(km/時)

（２）川の上流にあるA地点と、下流にあるB地点は18km離れています。船で移動するとき、A地点からB地点までは50分かかり、B地点からA地点までは75分かかります。静水時の船の速さは時速何kmですか。ただし、川の流れの速さは一定であるとします。

答え（２）

時速18km

解き方（２）

川を下る速さは、
18(km) ÷ \(\dfrac{50}{60}\)(時)
= 18 × \(\dfrac{60}{50}\)
= 18 × \(\dfrac{6}{5}\)
= \(\dfrac{108}{5}\) = 21.6(km/時)
川を上る速さは、
18(km) ÷ \(\dfrac{75}{60}\)(時)
= 18 × \(\dfrac{60}{75}\)
= 18 × \(\dfrac{4}{5}\)
= \(\dfrac{72}{5}\) = 14.4(km/時)
よって静水時の船の速さは、
( 21.6 + 14.4 ) ÷ 2 = 36 ÷ 2 = 18(km/時)

（３）静水時で時速8kmの船が、川に沿って4km離れたA町とB町の間を往復しています。A町からB町までは24分かかります。B町からA町までは何分かかりますか。

答え（３）

40分

解き方（３）

A町からB町に向かう速さは、
4 ÷ \(\dfrac{24}{60}\)
= 4 × \(\dfrac{60}{24}\)
= 4 × \(\dfrac{5}{2}\) = 10(km/時)
静水時の船の速さより速いことから、A町からB町は川を下っており、川の流れの速さは 10 – 8 = 2(km/時) とわかった。
B町からA町へ向かう（川を上る）速さは 8 – 2 = 6(km/時) となるので、かかる時間は、
4 ÷ 6 = \(\dfrac{2}{3}\)(時間) = 40(分)

問２

（１）川の下流にあるA町と18km上流にあるB町を往復する船があります。船は7時にA町を出発し、B町へ向かいました。また、船はB町に着くと30分間止まります。グラフは、船の運航の様子をあらわしたものです。ただし、川の流れは一定であるとします。

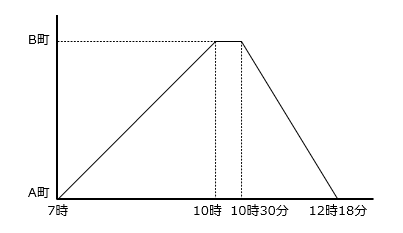
① この船の静水時の速さは時速何kmですか。

答え（１）- ①

時速8km

解き方（１）- ①

A町からB町に向かう（川を上る）速さは、
18 ÷ ( 10 – 7 ) = 18 ÷ 3 = 6(km/時)
B町からA町へ向かう（川を下る）のにかかる時間は、
1時間48分 = \(\dfrac{9}{5}\)(時間)
速さは、
18 ÷ \(\dfrac{9}{5}\) = 18 × \(\dfrac{5}{9}\) = 10(km/時)
よって、静水時の船の速さは、( 6 + 10 ) ÷ 2 = 8(km/時)

② ある日、B町からA町にもどる途中でエンジンが故障し、船が止まってしまいました。エンジンの修理に何分間かかかったため、A町には12時30分にもどってきました。修理にかかった時間は何分間ですか。ただし、修理中も船は川に流されているものとします。

答え（１）- ②

15分間

解き方（１）- ②

もどるのにかかった時間は120分(=2時間)。
川の流れの速さは ( 10 – 6 ) ÷ 2 = 2(km/時)
川の流れのみで2時間進んだ距離は、2(km/時) × 2(時間) = 4(km)
船の速さのみで進んだ距離は、18 – 4 = 14(km)
14(km)を船の速さ(8km/時)で進むと、14 ÷ 8 = 1 \(\dfrac{3}{4}\) 時間かかる。
2時間かかった時間のうち、1 \(\dfrac{3}{4}\) 時間のみ船の速さで進んだことになる。
2 – 1 \(\dfrac{3}{4}\) = \(\dfrac{1}{4}\) ・・・船が進んでいない時間
よって、 \(\dfrac{1}{4}\) = 15分間

（２）分速15mで流れている川を、兄は下流のA地点から上流のB地点へ、弟はB地点からA地点へ船で一定の速さで進みます。グラフはその様子をあらわしています。流れがないときの2人の船の速さは同じです。

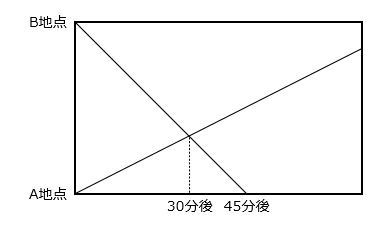
① 流れがないときの船の速さは分速何mですか。

答え（２）- ①

分速45m

解き方（２）- ①

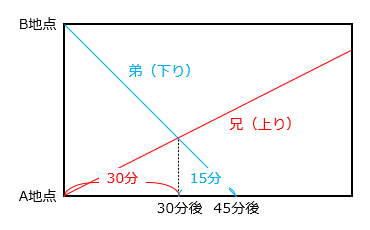
A地点から兄が弟と出会うまで30分間で進んだ距離と、弟が兄と出会ってからA地点に着くまで15分間で進んだ距離は等しい。したがって、兄と弟の進む速さの比は \(\boxed{1}\) ： \(\boxed{2}\) である。
川の流れの速さは、( \(\boxed{2}\) – \(\boxed{1}\) ) ÷ 2 = \(\boxed{0.5}\)
\(\boxed{0.5}\) が分速15mにあたるので、 \(\boxed{1}\) = 30となる。
そして、
静水時の船の速さは、( \(\boxed{1}\) + \(\boxed{2}\) ) ÷ 2 = \(\boxed{1.5}\)
よって、 \(\boxed{1.5}\) × 30 = 45(m/分)

【別解】兄と弟の進む速さの比は1：2、流れがないときの船の速さを□(m/分)とすると、
□ – 15：□ + 15 = 1：2
2 × ( □ – 15 ) = □ + 15
2 × □ – 30 = □ + 15
2 × □ – □ = 15 + 30
□ = 45(m/分)

② 2人の船が出会ったのはA地点から何mの地点ですか。

答え（２）- ②

900m

解き方（２）- ②

①より、兄の船が進む速さは 45 – 15 = 30(m/分) なので、
30 × 30 = 900(m)

③ A地点からB地点までは何mですか。

答え（２）- ③

2700m

解き方（２）- ③

①より、弟の船が進む速さは 45 + 15 = 60(m/分) なので、
60 × 45 = 2700(m)

（３）分速20mで流れる川があります。この川の下流と上流に6.4km離れたA地点とB地点があります。A地点とB地点を同時に出発した2つの船が出会うのは、出発してから何分後ですか。ただし、2つの船の静水時の速さは同じで、分速100mとします。

答え（３）

32分後

解き方（３）

A地点からB地点に向かう（上り）速さは 100 – 20 = 80(m/分)
B地点からA地点に向かう（下り）速さは 100 + 20 = 120(m/分)

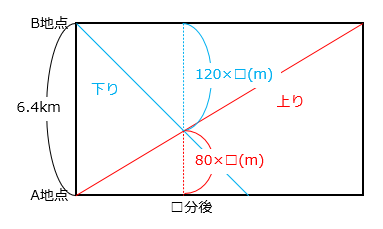
旅人算で求める
6400(m) ÷ ( 80 + 120 ) = 32(分)

【別解】式で求める
出会う時間を□とすると、
80 × □ + 120 × □ = 6.4 × 1000
200 × □ = 6400
□ = 32(分後)

（４）静水時に時速12kmで進む2台の船㋐、㋑があります。ある川に沿って180km離れている2地点A、Bがあり、この川はBからAに向かって流れています。BからA側に21.6km離れたC地点までの川の流れの速さは時速3kmですが、C地点より下流は流れの速さが時速2kmになっています。このとき、船㋐と㋑はそれぞれAからB、BからAへ同時に出発しました。

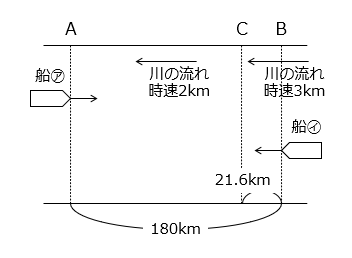
① 船㋑がC地点に着いたとき、船㋐はA地点から何kmの地点にいますか。

答え（４）- ①

14.4km

解き方（４）- ①

BからCの間を船㋑が進む速さは 12 + 3 = 15(km/時)
よって、船②がC地点に着くのにかかる時間は 21.6 ÷ 15 = 1.44(時間)
船㋐の進む速さは 12 – 2 = 10(km/時)より、船②がC地点に着いたときの船㋐のA地点からの距離は、
10 × 1.44 = 14.4(km)

② 船㋐と㋑がすれ違うのは、Aから何kmの地点ですか。

答え（４）- ②

74.4km

解き方（４）- ②

CからAの間を船㋑が進む速さは 12 + 2 = 14(km/時)

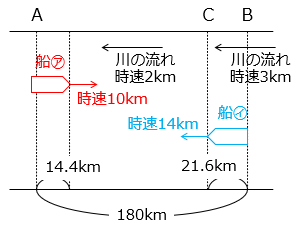
船㋐と㋑が出会う旅人算として求めると
船㋑がC地点に着いたとき船㋐は①よりAから14.4kmのところにいる。
船㋐と㋑の隔たり(距離)は、180 – 21.6 – 14.4 = 144(km)
144 ÷ ( 10 + 14 ) = 6(時間)
このとき船㋐のA地点からの距離は、
14.4 + 10 × 6 = 74.4(km)

【別解】式で求める
船㋑がC地点に着いた後、船Aとすれ違う時間を□時間後とすると、
10 × □ + 14 × □ = 180 – ( 14.4 + 21.6 )
24 × □ = 144
□ = 6(時間後)
このとき船㋐のA地点からの距離は、
14.4 + 10 × 6 = 74.4(km)